1.2.2 Принцип регулирования по возмущению

Самостоятельно. Литература: Савичев С.С. «Автоматизация производственных» (среди дополнительной литературы номер первый).

Этот принцип может быть использован и в системах стабилизации, и в системах программного регулирования, и в системах автоматического слежения.

Изобразим структурную схему.

1.2.3 Принцип регулирования по ошибке (по отклонению)

Это самый широко применяемый принцип, обладает многими достоинствами. Может применяться во всех системах (как и предыдущий принцип).

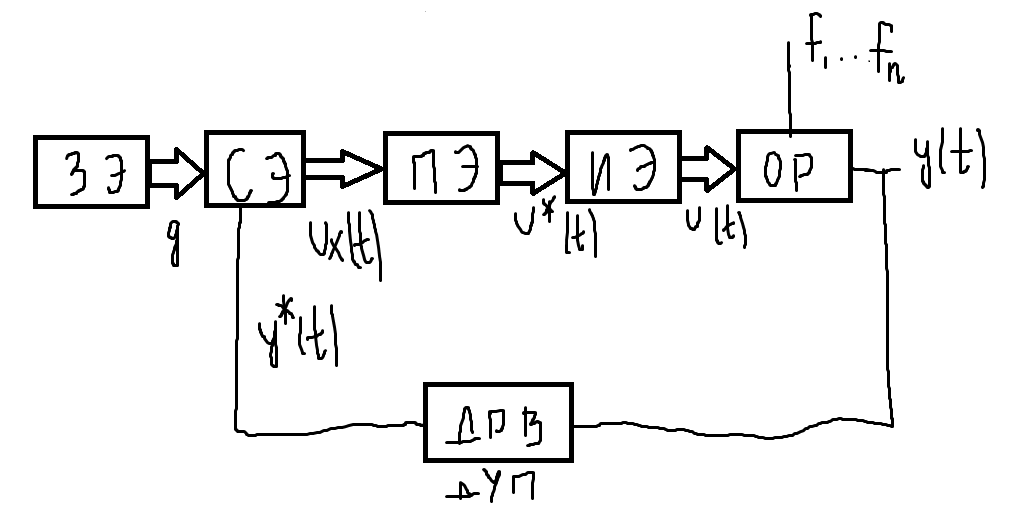
Изобразим структурную схему САР, в которой используется принцип. Рассмотрим на примере стабилизации.

Ошибка и отклонение связаны между собой, как видно. Обратные величины.

Для идеального ДРВ математическая модель имеет следующий вид:

Для идеального СЭ схема будет такая:

Теперь управляющее устройство состоит из двух элементов – сравнивающего элемента и преобразовательного элемента.

Для этой системы g(t) = const.

f₁ и f₂ приблизительно const во время работы, чтобы обеспечивать требуемое значение выходной величины. Пример – у профессионального магнитофона 5 скоростей записи, выбираем что-либо из них.

В паспортных данных задают диапазон возмущающих воздействий f_1min-f_1max, f_2min-f_2max.

Теперь надо изменить модель объекта регулирования.

Установившийся режим – статический.

Построим структурную модель для установившегося режима, а точнее для статического режима.

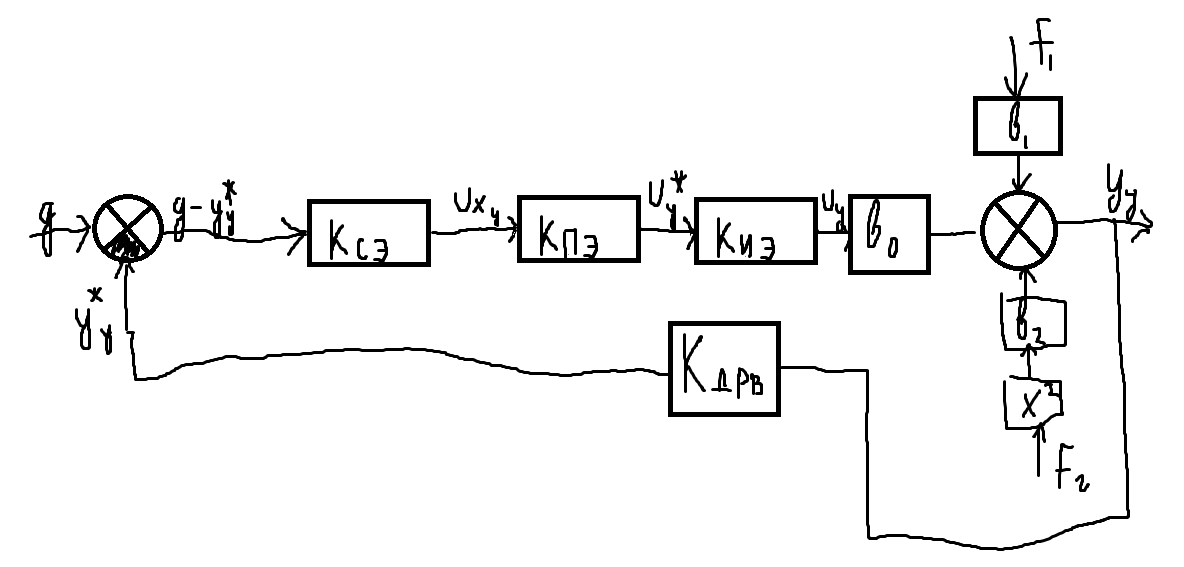
Для статического режима:

(1.19)

Это уравнение статики. Коэффициенты постоянные.

Рассмотрим статическую ошибку.

y_тр задано и является постоянным. Надо рассчитать y_y.

Хоть и имеется возведение в квадрат, всё равно применим принцип суперпозиции. Применим его.

Есть 4 составляющих.

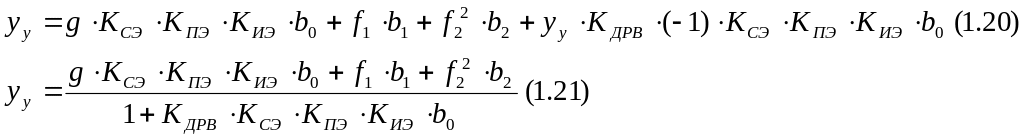
09.10.2012

Разомкнутая САР – размыкание мысленное. На входе этой системы размыкается ОС и в качестве входной величины рассматривается задающее воздействие, а выходной величиной рассматривается сигнал на выходе датчика. Тогда если известно задающее воздействие g(t), то выход находится простым перемножением с коэффициентом передачи (этот коэффициент служит, чтобы находить амплитуду выходного сигнала, если задана амплитуда входного сигнала).

Из определения видно, что данная система является статической. Сие можно доказать.

1) Допустим, что f₁ = f₁₁ = const. f₂ = f₂₁ = const. При этом y_уст = y_тр.

2) Даём положительное приращение Δf₁. В этом случае уже f₁₂ = f₁₁ + Δf₁. f₂ = f₂₁ неизменно. Значит, y_у увеличится. Возникнет статическая ошибка (разница между требуемым и установившимся значениями не станет нулевой, она станет меньше нуля). Всё, доказали.

Рассмотрим переходной процесс, работу этой системы в переходном режиме.

В момент включения в работу системы допустим, что y = 0. Тогда сигнал на выходе датчика будет равен тоже нулю. А чему будет равен сигнал ошибки?

Допустим, что g = g₀. Таким образом, x = g₀*К_СЭ. Таким образом, получается большой сигнал ошибки. На практике этот сигнал обычно ограничивают (стабилитроны etc), чтобы в первый момент времени не возникали больше токи и так далее. Но всё равно сразу же к двигателю (если двигатель) будет приложено достаточно большое напряжение, и двигатель будет разгоняться с большим ускорением (это хорошо, за счёт этого сокращается время переходного процесса). С ростом регулируемой величины сигнал на выходе датчика возрастает, а сигнал ошибки начинает уменьшаться. Этот сигнал ошибки сначала неизменен, а наступая с определённого момента t₁ этот сигнал будет максимальным.

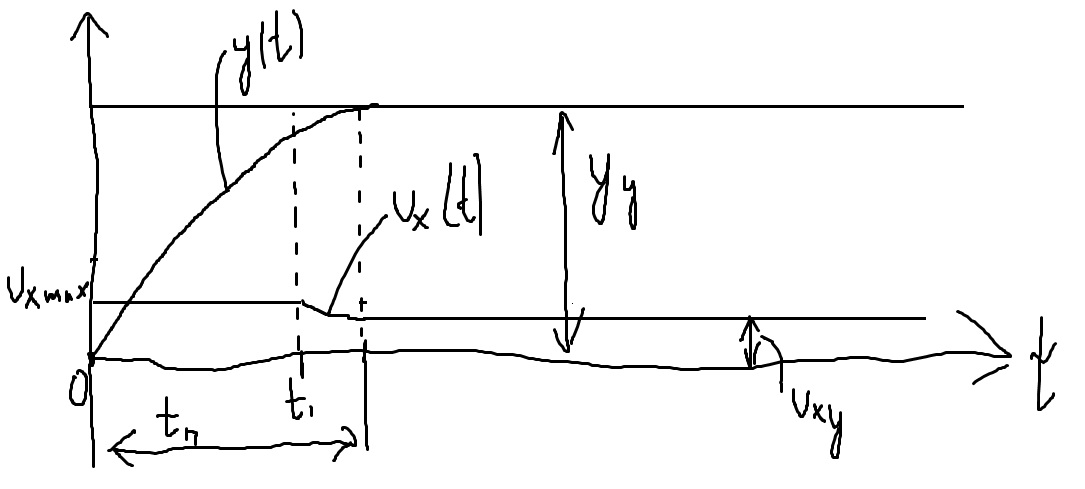
g выбирают, исходя из того, чтобы при f₁ = f_{1 сред} и f₂ = f_{2 сред} выполнялось равенство y_y = y_тр.

Берут средние, потому что таким образом осуществляется настройка.

Выведем формулу статической ошибки x_ст = F(f₁, f₂).

Надо знать конкретное значение g.

Вспоминаем формулу 1.21:

Подставим её вместо y_тр, вместо f₁ f_{1 сред}, вместо f₂ f_{2 сред} (сделать дома).

Надо найти статическую ошибку x_ст = y_тр - y_уст.

Подставим 1.22 в формулу x_ст.

f_ср находится с использованием паспортных данных (где заданы максимальное и минимальное значения возмущающих воздействий).

Если бы не было ОС, то был бы только числитель (по задающему воздействию).

Достоинства:

1) САР реагирует на изменение любого возмущения и параметра преобразовательного элемента, исполнительного элемента и объекта регулирования (в регулировании по возмущению ограниченное число датчиков). Остальные коэффициенты упущены, потому что ключевые элементы – преобразовательный, исполнительный, объект регулирования.

2) В статических системах автоматической стабилизации статическую ошибку можно уменьшить до допустимого значения путём увеличения коэффициента передачи разомкнутой САР.

Недостаток:

1) САР склонна к неустойчивости (к расходящимся процессам). Пояснение: используется отрицательная обратная связь. Надо спроектировать, чтобы она была на всех частотах. Но стоит только появиться положительной обратной связи, образуется генератор. Раскачка пойдёт от возмущений, пульсаций, помех. Этого недостатка нет в предыдущих двух принципах регулирования. Чем больше К_р, тем больше вероятность, что система будет неустойчивой.

16.10.2012