1.1.2 Понятие регулирования

Регулирование – изменение во времени физической величины по требуемому закону в установившемся режиме, который наступает после окончания переходного процесса, связанного с введением в работу объекта управления (ОУ). Но также надо иметь в виду, что обеспечение постоянства физической величины рассматривается как частный случай изменения.

В систему регулирования не входит ПР. Регулирование – это частный случай управления, когда целью является изменение этой величины по заданному закону.

Теория регулирования (ОР, РУ и т.п.).

11.09.2012

Требуемый закон – это функция времени y_тр(t). Например, регулируемая величина – угловая скорость вала двигателя видеомагнитофона Ω. Например, требуется Ω_тр = 100 рад/c = const; частота съёмки киносъёмочной камеры ν_тр(t) = ν₀ +at (для замедления движения); какое-то устройство надо проверить на механическую тряску, перемещение по вертикальной платформы S_тр(t) = S_max*cos(2*pi*f_{платформы}*t). Ещё бывает, чтобы какая-нибудь величина изменялась в зависимости не от времени, а, например, от диаметра рулона.

Установившийся режим:

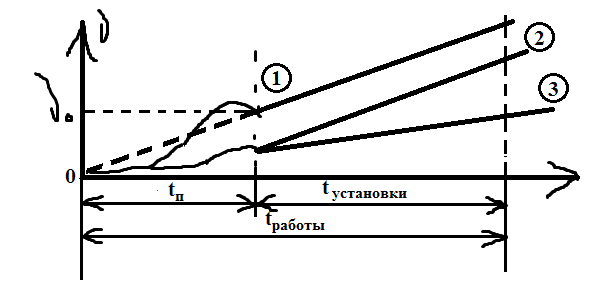
Из определения регулирования вытекает, что САР должна быть в первую очередь очень точной. Точность работы САР обычно оценивают по установившейся ошибке регулирования x₁(t) – разности между требуемым значением регулируемой величины и текущим значением в установившемся режиме:

(sic!)

Из рисунка 1: 1: x_у(t) = 0; 2: x_у(t) = const; 3: x_у(t) ≠ const.

Установившаяся ошибка – это основной показатель качества работы САР. Она количественно характеризует это качество. Указывается в паспортных данных (обычно).

Из определения вытекает, что требуемый закон должен быть задан. В задачу системы регулирования эта задача не входит, программатора нет в составе системы. На практике этот закон y_тр(t) уже закладывается при проектировании. Это программа регулирования. Если их несколько, то оператор (человек) должен эту программу выбрать.

Изобразим структурную схему САР.

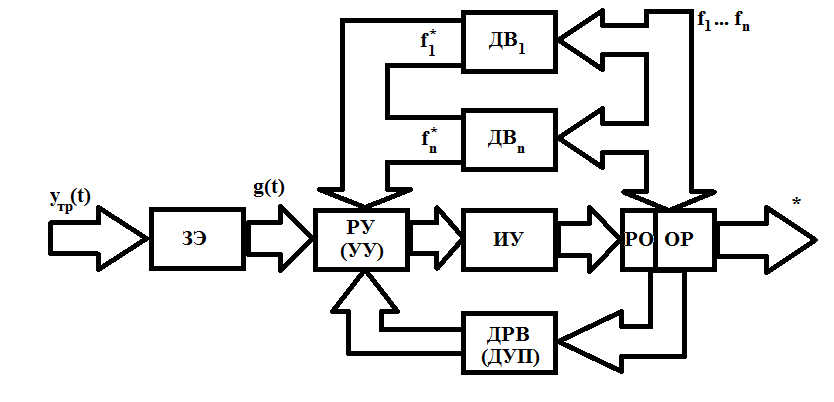
ЗЭ – задающий элемент, проектируется.

РУ – регулирующее устройство.

ИУ – исполнительное устройство.

РО – регулируемый орган.

ОР – объект регулирования.

ДРВ – датчик регулируемой величины.

18.09.2012

Для системы САР рассматривают ещё дополнительные показатели качества, которые характеризуют её работу в установившемся режиме, который наступает после включения системы. К ним относятся:

- время переходного процесса t_п;

- перерегулирование σ.

Для нахождения численных значений этих критериев на вход системы (т.е. на выходе задающего элемента) формируется ступенчатое воздействие (какое-то число, умноженное на единичную ступенчатую функцию). Изобразим график:

Теоретически время переходного процесса равно бесконечности.

Пусть поведение рассматриваемой системы изменяется по следующему закону:

(2)

Практически за время переходного процесса принимают время от начала переходного процесса до момента, когда отклонение y(t)-y_уст по модулю меньше Δ.

Перерегулирование σ – это относительное превышение максимальным значением регулируемой величины y_max установившегося значения y_у.

Для хороших САР требуется, чтобы регулирование находилось в диапазоне от 10% до 30%.