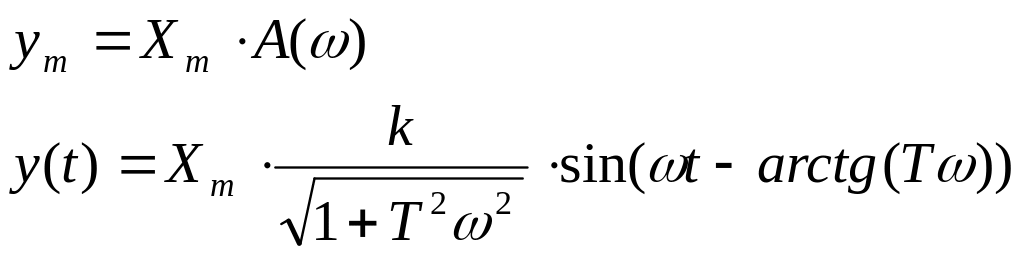- •1 Назначение, принципы использования и построения устройств радиоавтоматики, элементов устройств радиоавтоматики 5
- •2 Математические модели непрерывных и дискретных линейных объектов и систем 38
- •3 Передаточные функции, частотные характеристики 45
- •4 Математические модели устройств радиоавтоматики, методы их анализа, синтез оптимальных структур 56
- •Радиоавтоматика Введение
- •1. (Системы аудио-видео автоматики.)
- •1 Назначение, принципы использования и построения устройств радиоавтоматики, элементов устройств радиоавтоматики
- •1.1 Основные понятия об управлении, регулировании
- •1.1.1 Понятия управления
- •1.1.2 Понятие регулирования
- •1.1.3 Классификация сар по требуемому закону изменения регулируемой величины в установившемся режиме
- •Системы автоматической стабилизации.
- •Системы программного регулирования.
- •Следящие системы.
- •1.1.4 Классификация сар по точности работы в статическом режиме
- •1.1.5 Системы автоматического контроля
- •1.1.10 Непрерывные, дискретные, цифровые, аналоговые системы автоматики
- •1.1.11 Линейные и нелинейные системы автоматики
- •1.2 Основные принципы управления
- •1.2.1 Принцип регулирования по задающему воздействию
- •1.2.2 Принцип регулирования по возмущению
- •1.2.3 Принцип регулирования по ошибке (по отклонению)
- •1.2.4 Комбинированный принцип регулирования
- •1.2.5 Принцип адаптивного управления
- •1.2.6 Принцип иерархии в управлении
- •1.3 Примеры систем радиоавтоматики
- •1.3.1 Статическая сар угловой скорости
- •1.3.2 Астатическая сар угловой скорости
- •1.3.3 Система автоматической подстройки частоты (сапч)
- •1.3.4 Система фазовой автоподстройки частоты (сфапч)
- •2 Математические модели непрерывных и дискретных линейных объектов и систем
- •2.1 Математические модели линейных стационарных непрерывных элементов
- •2.2 Математические модели линейных стационарных дискретных элементов
- •3 Передаточные функции, частотные характеристики
- •3.1 Передаточные функции, временнЫе и частотные характеристики линейных стационарных непрерывных элементов
- •3.1.1 Передаточные функции непрерывных элементов
- •3.1.2 ВременнЫе характеристики непрерывных элементов
- •3.1.3 Частотные характеристики элементов
- •3.2 Передаточные функции, частотные характеристики линейных стационарных дискретных элементов
- •3.2.1 Передаточные функции дискретных элементов
- •3.2.2 Частотные характеристики дискретных элементов
- •4 Математические модели устройств радиоавтоматики, методы их анализа, синтез оптимальных структур
- •4.1 Математические модели линейных стационарных непрерывных и дискретных систем радиоавтоматики
- •4.1.1 Передаточные функции непрерывных систем радиоавтоматики
- •4.1.2 Передаточные функции дискретных систем радиоавтоматики
- •4.2 Методы анализа линейных систем радиоавтоматики
- •4.2.1 Построение кривых переходного процесса в линейных стационарных непрерывных сар
- •Нахождение дифференциального уравнения сар по заданным передаточным функциям сар
- •4.2.2 Построение кривых переходного процесса для линейных стационарных дискретных сар
- •Вопросы к экзамену
3.1.2 ВременнЫе характеристики непрерывных элементов
Временные характеристики являются реакциями элементов на типовые входные воздействия. С их помощью можно сравнивать поведение элементов в переходных процессах. Зная это поведение, можно объяснить принцип действия элемента, а при проектировании систем за счёт ввода в неё определённых элементов, добиться нужного поведения.
Широкое распространение получили две временные характеристики, которые позволяют характеризовать переходные процессы:
1. Переходная функция h(t).
2. Импульсная переходная функция (импульсная характеристика, функция веса для интеграла Дюамеля) w(t).
Переходная функция элемента.
27.11.2012
Найдём переходную функцию, используя передаточную функцию элемента:
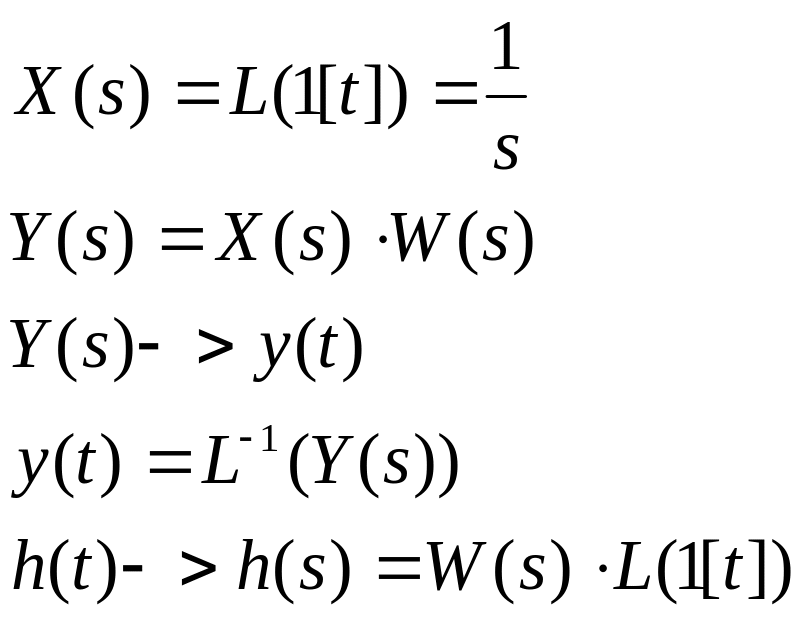
![]()
Зададимся передаточной функцией. Пусть она будет представлять собой передаточную функцию апериодического звена первого порядка.
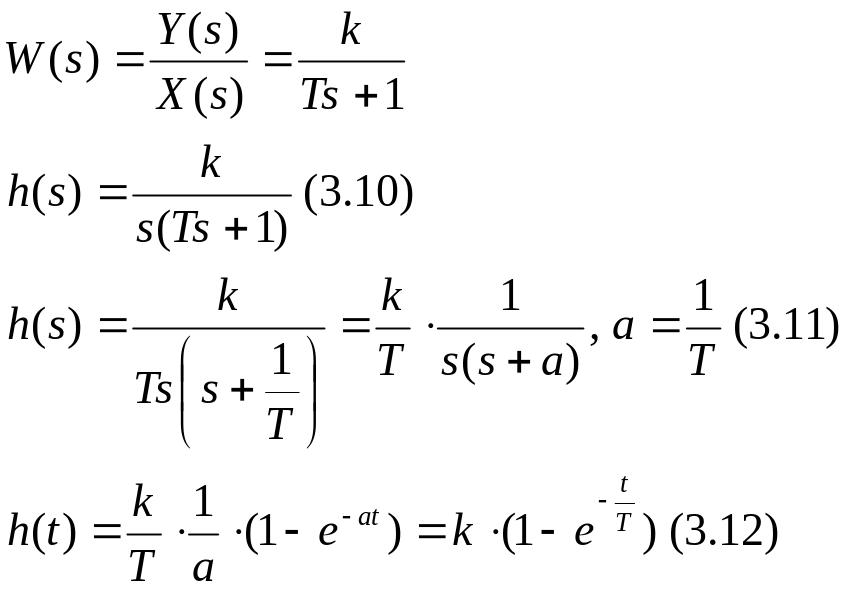
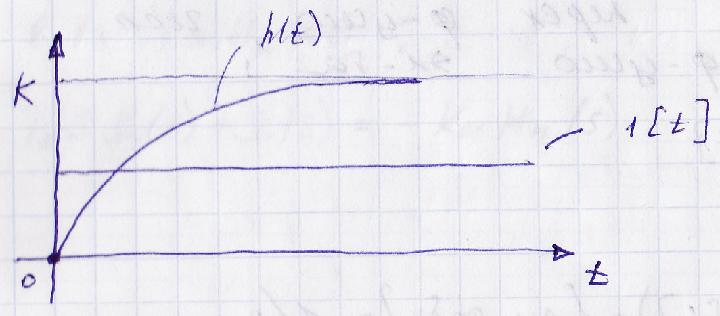
Импульсная функция элемента (функция веса)
Это реакция элемента на дельта-функцию Дирака. Дельта-функция имеет вес (площадь), равный единице.
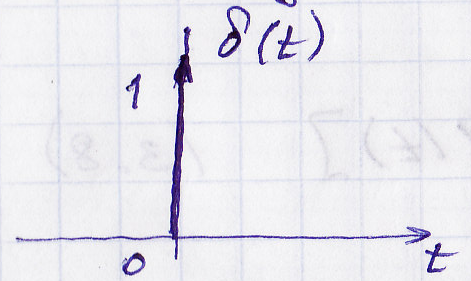
![]()
w(t) – импульсная характеристика.
![]()
![]()
![]()
Используем таблицу.
![]()
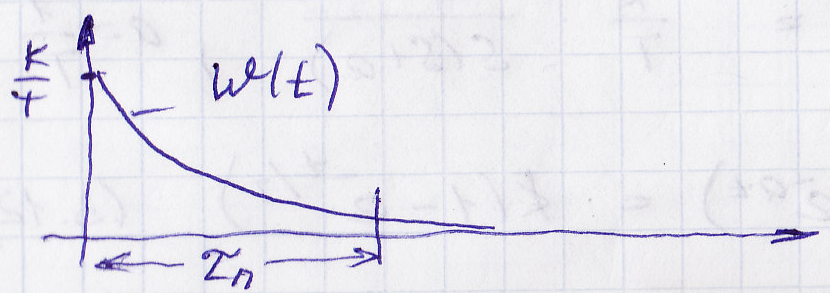
Импульсная функция элемента обладает следующими свойствами:
1) Импульсная функция равна нулю при t <0 – условие физической реализуемости.
2)
![]()
Интервал времени, на котором w отлично от нуля, называется памятью элемента.
Практически надо задаваться конечным значением τп (теоретически оно равно бесконечности), брать примерно 0,1 от максимального значения.
Для стационарных элементов w(t) зависит от разности времени наблюдения выходной величины и времени приложения дельта-функции.
Если какой-то элемент включить в работу в момент времени t = 10 с (как пример), то будет такая же экспонента, но сдвинутая во времени.
3.1.3 Частотные характеристики элементов
Для изучения поведения в установившихся режимах в качестве типового входного воздействия рассматривают гармоническое воздействие.
![]()
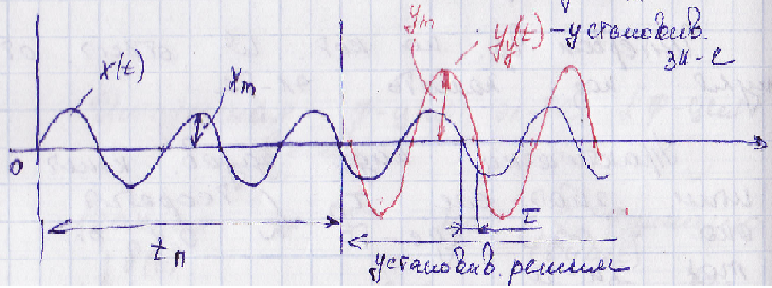
Для линейного стационарного установившегося режима выходная величина также будет изменяться по гармоническому закону, но она будет сдвинута по фазе (останется с той же самой частотой).
![]()
Это справедливо только для линейных стационарных элементов.
![]()
Соответственно, остаются три параметра – амплитуда, частота, фаза.
Для большинства элементов при сохранении амплитуды входной величины Xm для разных частот наблюдаются разные амплитуды выходной величины Ym и разные фазовые сдвиги φ.
Для нахождения параметров гармонической выходной величины (ym, φ) необходимо знать комплексный коэффициент передачи для заданной частоты ω.
Самый простой путь – связанный с использованием передаточной функции (для нахождения ym, φ).
Комплексный коэффициент передачи – отношение комплексных амплитуд выходной и входной величин.
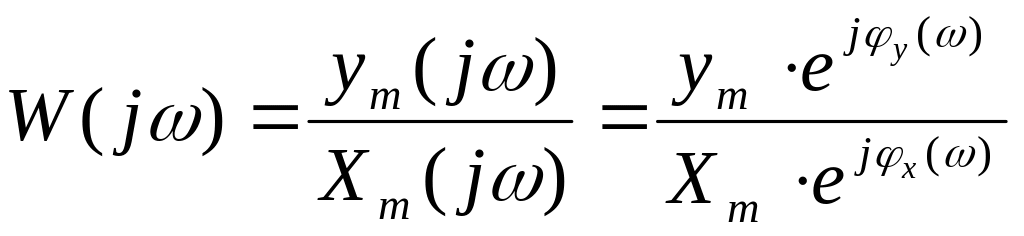
Если взять φх = 0, то:
![]()
![]()
Вещественная частотная характеристика – зависимость вещественной части от частоты.
В автоматике отношение реальных амплитуд ym и Xm обозначают буквой А и называют коэффициентом передачи элемента.
![]()
![]()
![]() - АЧХ.
- АЧХ.
![]() - ФЧХ.
- ФЧХ.
Зададимся:
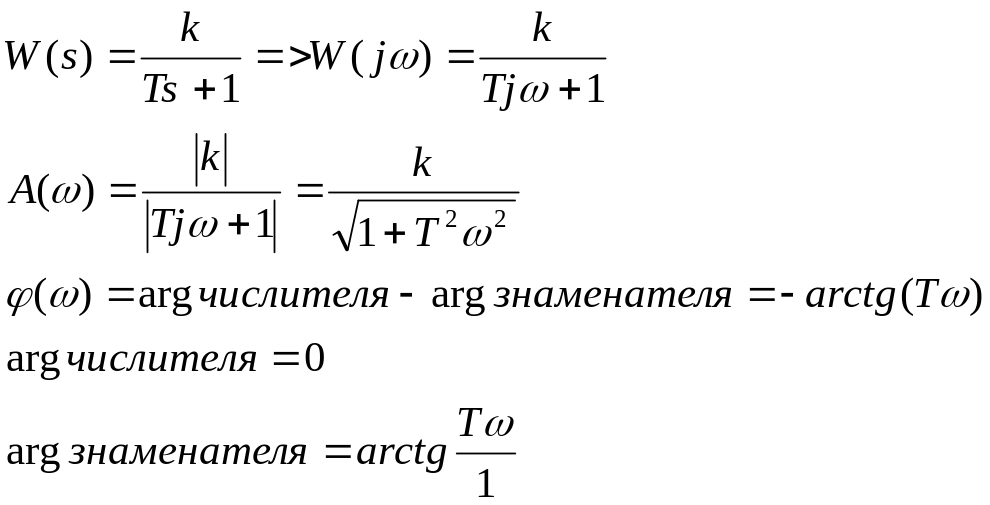
Найдём ym, если нам известно Xm: