
- •Екзамінаційний білет № 1
- •Екзамінаційний білет № 2
- •5. Розіграти чотири можливих значення неперервної випадкової величини , розподіленої рівномірно в інтервалі
- •6. Задана матриця переходу ланцюга маркова .Знайти матрицю переходу . Екзамінаційний білет № 3
- •5. Розіграти чотири можливих значення неперервної випадкової величини , розподіленої рівномірно в інтервалі
- •6. Задана матриця переходу ланцюга маркова .Знайти матрицю переходу . Екзамінаційний білет № 4
- •Екзамінаційний білет № 5
- •Екзамінаційний білет № 6
- •5. Розіграти чотири можливих значення неперервної випадкової величини , розподіленої рівномірно в інтервалі
- •6. Задана матриця переходу ланцюга маркова .Знайти матрицю переходу . Екзамінаційний білет № 7
- •5. Розіграти чотири можливих значення неперервної випадкової величини , розподіленої рівномірно в інтервалі
- •6. Задана матриця переходу ланцюга маркова .Знайти матрицю переходу . Екзамінаційний білет № 8
- •5. Розіграти чотири можливих значення неперервної випадкової величини , розподіленої рівномірно в інтервалі
- •6. Задана матриця переходу ланцюга маркова .Знайти матрицю переходу . Екзамінаційний білет № 9
- •5. Розіграти чотири можливих значення неперервної випадкової величини , розподіленої рівномірно в інтервалі
- •6. Задана матриця переходу ланцюга маркова .Знайти матрицю переходу . Екзамінаційний білет № 10
- •5. Розіграти чотири можливих значення неперервної випадкової величини , розподіленої рівномірно в інтервалі
- •6. Задана матриця переходу ланцюга маркова .Знайти матрицю переходу .
МІНІСТЕРСТВО ОСВІТИ І НАУКИ,МОЛОДІ ТА СПОРТУ
ДЕРЖАВНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД
«КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ
ІМЕНІ ВАДИМА ГЕТЬМАНА»
Навчальний предмет : Дослідження операцій
Спеціальність: ________ Семестр 5
Екзамінаційний білет № 1
Оцінка похибки метода Монте-Карло нормально розподіленої випадкової величини з відомим середнє квадратичним відхиленням. З надійністю
 знайти верхню границю помилки
знайти верхню границю помилки
 ,
якщо для оцінки математичного сподівання
розподіленої нормально випадкової
величини
,
якщо для оцінки математичного сподівання
розподіленої нормально випадкової
величини
 з
відомим середнє квадратичним відхиленням,
що дорівнює
з
відомим середнє квадратичним відхиленням,
що дорівнює
 було розіграно 50 можливих значень
.
було розіграно 50 можливих значень
.
2. Середнє число вимог в черзі з одним каналом. Перед вікном каси відділення банку кожного дня з'являється 50 людей (каса відкрита протягом 8 годин в день).Одне вікно каси може обслуговувати в середньому 10 людей за годину. Припускаючи, що потік пуасонівський і розподіл часу розподілен за показниковим законом, обчислити середню довжину черги у вікна і ймовірність черги довжина якої більше 2 людей.
3. Розіграти 6 можливих значень дискретної випадкової величини , закон розподілу якої задан у вигляді таблиці
-
Х
2
10
18
р
0,22
0,17
0,61
для визначенності прийняти випадкові числа 0,32;0,17;0,9;0,05;0,97;0,87.
4. За заданою
матрицею переходу
 побудувати
ланцюг Маркова.
побудувати
ланцюг Маркова.
5. Розіграти
чотири можливих значення неперервної
випадкової величини
,
розподіленої рівномірно в інтервалі
![]()
6. Задана
матриця переходу ланцюга маркова
![]() .Знайти
матрицю переходу
.Знайти
матрицю переходу
![]() .
.
Екзамінаційний білет № 2
Оцінка похибки метода Монте-Карло нормально розподіленої випадкової величини з невідомим середнє квадратичним відхиленням. З надійністю знайти верхню границю помилки , якщо для оцінки математичного сподівання розподіленої нормально випадкової величини було розіграно 40 можливих значень і по ним було знайдено «виправлене» середнє квадратичне відхилення

Пуасонівський закон розподілу потіка вимог. Тривалість обслуговування
 розподілена
за законом Пуасона з числом вимог,
рівним 10.Записати закон розподілу
розподілена
за законом Пуасона з числом вимог,
рівним 10.Записати закон розподілу

Задани ймовірності трьох подій:
 ,
які утворюють повну групу подій:
,
які утворюють повну групу подій:
 ,
,
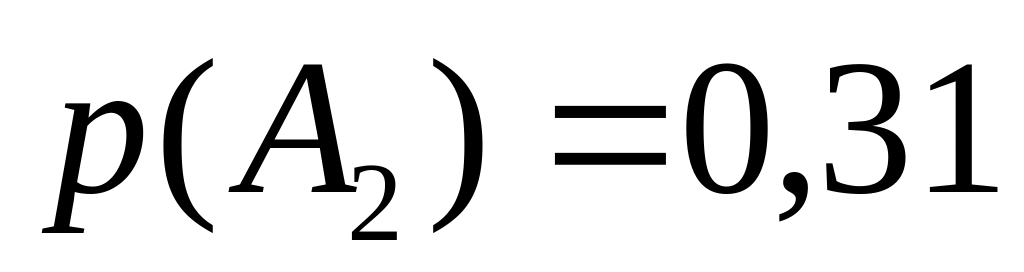 ,
,
 .
Розіграти п'ять випробувань, в кожному
з яких з'явиться одно з трьох розглядаємих
подій.
.
Розіграти п'ять випробувань, в кожному
з яких з'явиться одно з трьох розглядаємих
подій.
За даною матрицею переходу
 побудувати
ланцюг Маркова.
побудувати
ланцюг Маркова.
5. Розіграти чотири можливих значення неперервної випадкової величини , розподіленої рівномірно в інтервалі
6. Задана матриця переходу ланцюга маркова .Знайти матрицю переходу . Екзамінаційний білет № 3
1.Розігрування протилежних подій методом Монте-Карло. Розіграти 6 випробувань
в кожному з яких подія
![]() з'являється
з ймовірністю
з'являється
з ймовірністю
![]()
2.Черга з одним каналом
обслуговування. Задані
параметри потоку
![]() ,
а параметр обслуговування
,
а параметр обслуговування
![]() .
Обчислити
.
Обчислити
![]() .
.
3.Задани
ймовірності чотирьох подій:
,
![]() ,
які утворюють повну групу подій:
,
які утворюють повну групу подій:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Розіграти десять випробувань, в кожному
з яких з'явиться одно з чотирьох
розглядаємих подій.
.
Розіграти десять випробувань, в кожному
з яких з'явиться одно з чотирьох
розглядаємих подій.
4.За даною матрицею переходу побудувати ланцюг Маркова.
