32. Какой оператор называется произведением линейного оператора на число?

Определение. Произведением линейного оператора на число называется оператор , определяемый равенством

где – любой вектор из .

Можно показать, что оператор является линейным оператором, а его матрица равна произведению числа на матрицу оператора , то есть .

33. Какой оператор называется произведением двух линейных операторов?

Определение. Оператор , переводящий вектор непосредственно в , называется произведением оператора на оператор , т.е. для всех векторов из имеет место равенство

при этом используется запись .

Можно показать, что произведение линейных операторов есть снова линейный оператор, а его матрица равна произведению матриц этих операторов, взятых в порядке, обратном действию операторов, то есть

34. Какой оператор линейного пространства называется сопряжённым по отношению к другому оператору линейного пространства?

Определение. Оператор называется сопряженным по отношению к оператору , если для любых векторов и из пространства выполняется равенство

Можно показать, что если оператор линейный, то у него существует единственный сопряженный оператор . При этом, если матрица

является матрицей оператора , то матрицей оператора . является матрица

Такая матрица называется сопряженной по отношению к матрице . При этом, если оператор действует из в то .

Можно показать, что имеет место следующая теорема.

35. Какой линейный оператор называется самосопряжённым (или Эрмитовым)?

Определение. Линейный оператор называется самосопряженным (или Эрмитовым), если он совпадает со своим сопряженным, т.е. если для любого вектора из выполняется равенство

Определение. Квадратная матрица называется симметричной, если для ее элементов выполняется равенство

36. Как происходит замена базиса в линейном пространстве?

Нетрудно заметить, что если в n-мерном пространстве имеется два базиса e₁, e₂, …, e_n и e’₁, e’₂, …, e’_n, то координаты произвольного вектора в одном базисе будут отличаться от координат того же вектора в другом базисе. Выясним, как связаны координаты произвольного вектора Х относительно базиса e₁, e₂, …, e_n с координатами этого вектора относительно базиса e’₁, e’₂, …, e’_n. Не уменьшая общности, рассмотрим трехмерный случай. Обозначив через x₁, x₂, x₃ и x’₁, x’₂, x’₃ координаты вектора относительно базисов e₁, e₂, e₃ и e’₁, e’₂, e’₃, соответственно, сможем написать:

, (1)

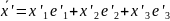. (2)

Для каждого из ортов e’1, e’2, e’3 имеют место следующие разложения в базис e1, e2, e3:

(3)

где - координаты вектора e’j в базисе e1, e2, e3.

Подставляя (3) в (2), получим:

x=(τ11x’1+τ12x’2+τ13x’3)e1+(τ21x’1+τ22x’2+τ23x’3)e2+(τ31x’1+τ32x’2+τ33x’3)en. (4)

Сравнивая теперь (1) с (4) и, учитывая единственность разложения вектора Х в базисе e₁, e₂, e₃, получим формулы, выражающие его координаты относительно базиса e1, e2, e3 через координаты базиса e’₁, e’₂, e’₃:

(5)

Если ввести в рассмотрение одностолбцовые матрицы , в матрицу

то систему (5) можно заменить одним матричным равенством Х=Т*Х’. Матрицу Т называют матрицей поворота координатной системы. Итак, координаты вектора x относительно базиса e1, e2, e3 линейно выражаются с помощью формулы (5) через его координаты относительно базиса e’1, e’2, e’3. Матрица системы (5) совпадает с матрицей, получающейся в результате транспонирования матрицы перехода от базиса e’1, e’2, e’3 к базису e1, e2, e3 (см. равенства 3).