Санкт-Петербургский Государственный Университет Информационных Технологий, Механики и Оптики

Кафедра Систем Управления и Информатики

Расчетно-исследовательская работа

«ИССЛЕДОВАНИЕ ПАРАМЕТРИЧЕСКОЙ ЧУВСТВИТЕЛЬНОСТИ ОБЪЕКТОВ И СИСТЕМ, СИНТЕЗ НЕАДАПТИВНЫХ И АДАПТИВНЫХ АЛГОРИТМОВ, ОБЕСПЕЧИВАЮЩИХ НЕОБХОДИМУЮ РОБАСТНОСТЬ ИХ ДИНАМИЧЕСКИХ ПОКАЗАТЕЛЕЙ»

по курсу «Адаптивное и робастное управление»

Вариант 10: А-А-В-В-А-А-А-А

Выполнила:	Студентка гр. 5145 Нибилица А.Ю.
Преподаватель:	Слита О.В.

Санкт-Петербург

2010 г.

Содержание

Введение. Постановка задачи……………………………………………………. 3

1. Построение МТЧ НОУ и результаты ее исследования…………………. 3

2. Построение МТЧ ДОУ и результаты ее исследования………………..... 6

3. Построение МТЧ СНС и результаты ее исследования…………………. 8

4. Построение МФМЧ и результаты ее исследования……………………. 15

5. Построение медианного МУ НОУ и оценка его результатов…………. 17

6. Синтез неадаптивного управления, обеспечивающего параметрическую инвариантность выхода СНС относительно неопределенности НОУ... 21

Заключение………………………………………………………………………. 22

Литература……………………………………………………………………….. 23

Введение. Постановка задачи

Дана передаточная функция «вход-выход» (ВВ) непрерывного объекта управления (НОУ):

,

,

где

.

1. Построение мтч ноу и результаты ее исследования

Передаточная функция вход-выход НОУ:

Перейдем к канонической управляемой форме:

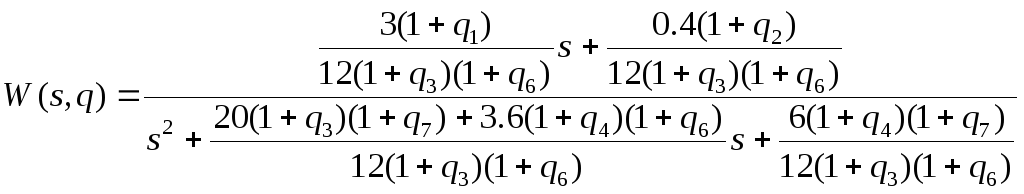
Для перехода к канонической управляемой форме воспользуемся формулами:

- представление НОУ:

,

,

.

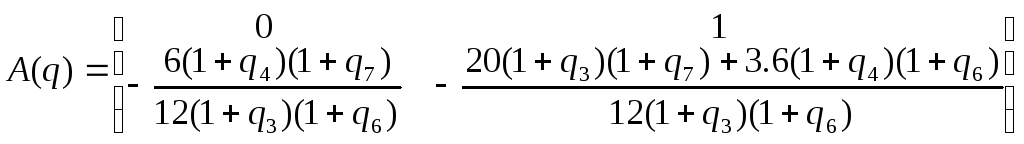Матрицы номинального ОУ:

, , .

Построение семейства моделей траекторной чувствительности:

Где , ,

,

,

,

.

и формирование семейства агрегированных систем:

где , , , .

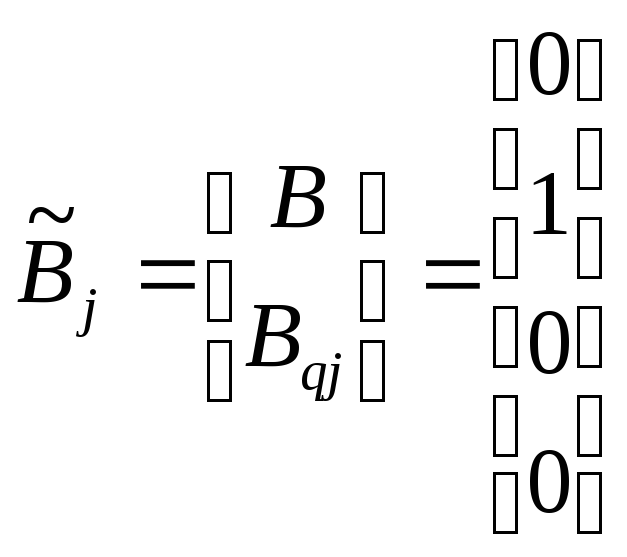Получим:

, , , ;

, , , ;

, , , ;

, , , ;

, , , ;

, , , ;

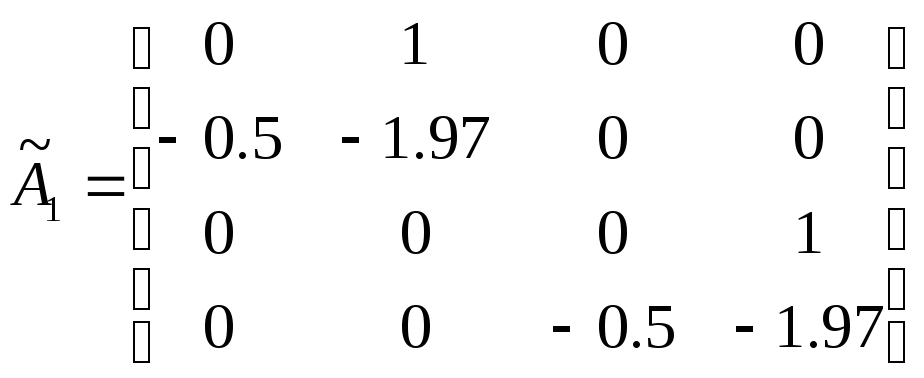Вычислим матрицы управляемости по функции траекторной чувствительности и их абсолютные нормы:

_,

,

,

,

,

,

.

В силу неравенства:

проранжируем параметры по потенциальной чувствительности:

.

То есть соответствующие сингулярные числа являются показателями того, на какое из дополнительных движений необходимо затратить большее управление для его асимптотической сходимости к нулю, таким образом чем больше сингулярное число, тем меньше затраты на управление для асимптотической сходимости дополнительного движения к нулю; верно и обратное.

2. Построение мтч доу и результаты ее исследования

Дан интервал дискретности и передаточная функция ОУ:

Переход к дискретному описанию ОУ осуществляется методом замены переменной разностью конечных малых, где производные заменяются по формулам:

тогда

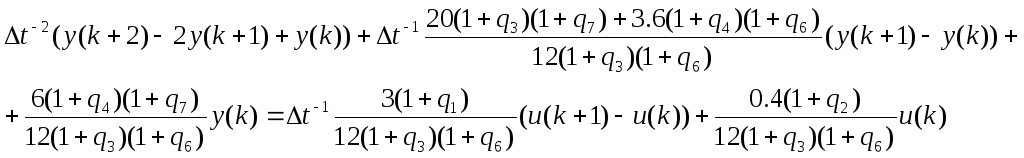
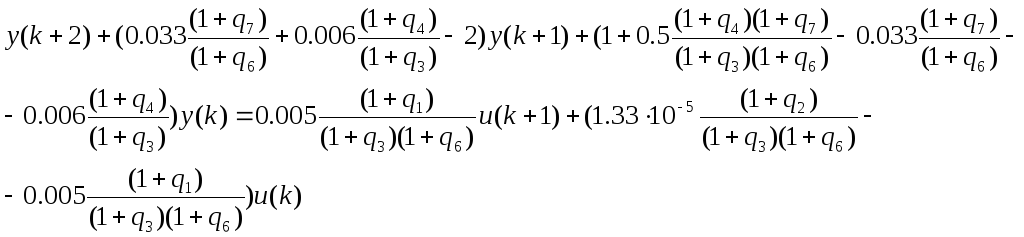
В конической управляемой форме матрицы ДОУ модели «Вход-Состояние-Выход» примут вид:

, .

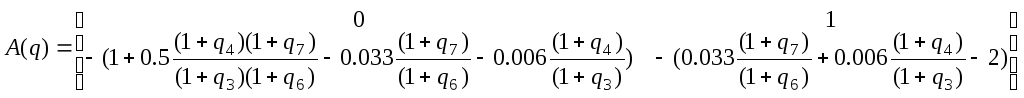
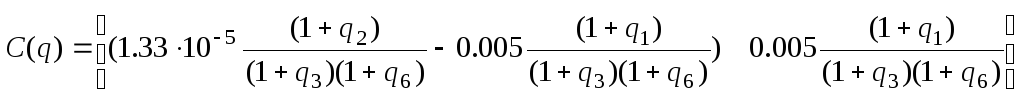Таким образом матрицы номинального дискретного ОУ примут вид:

.

Построим модель траекторной чувствительности к вариации интервала дискретности:

где ,

,

,

,

,

При условии, что q_j=0, j=(1,p), (1+q_p+1)=∆t – вариация интервала дискретности:

Построим агрегированный ОУ:

где , , .

Получим:

, ,

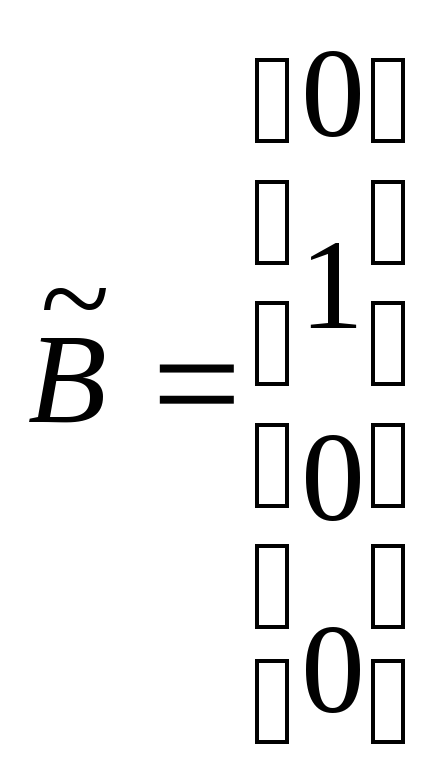3. Построение мтч снс и результаты ее исследования

Закон управления (ЗУ): должен доставлять системе

образованной объединением НОУ и ЗУ, с помощью:

- матрицы прямой связи по входу равенство входа и выхода в неподвижном состоянии при номинальных значениях параметров;

- матрицы обратной связи по состоянию при номинальных значениях параметров распределение мод Баттерворта с характеристической частотой .

Необходимо построить МТЧ спроектированной системы по каждому из параметров и для значения выделить доминирующие параметры по степени их влияния на величину перерегулирования и длительность переходного процесса.

Необходимо построить матрицу функций модальной чувствительности и выделить неблагоприятное сочетание вариаций параметров.

Имеем представление системы в канонической наблюдаемой форме «ВСВ»:

, ,

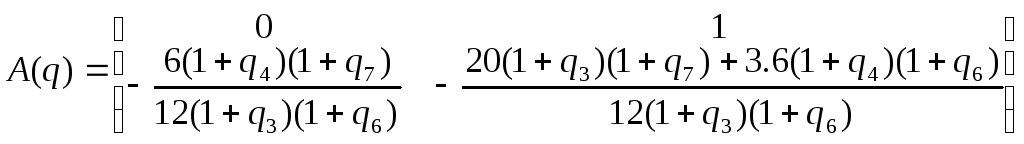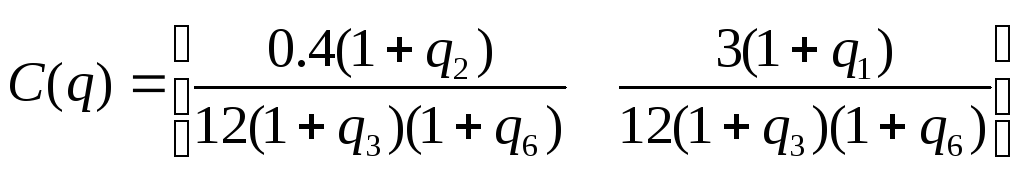
Для построения матрицы обратной связи по состоянию при номинальных значениях параметров используем полином Баттерворта 2го порядка:

Из требований к проектируемой системе найдем матрицы .

Сформируем характеристический полином: , на основе которого определим матрицу состояния желаемой системы:

Матрицу выхода находим на основе наблюдаемости пары (Г,Н): Н= [0 1].

Найдем матрицу преобразований из решения матричного уравнения Сильвестра: MГ–AM= –BН

_{тогда K=НM}^-1 _{K=[ -8.5 2.272]}

Найдем :

,

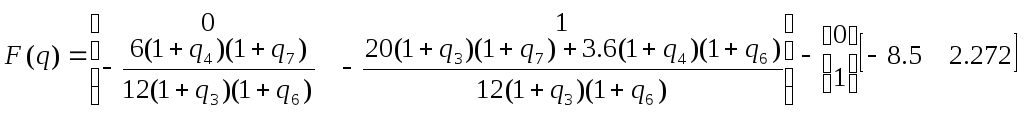
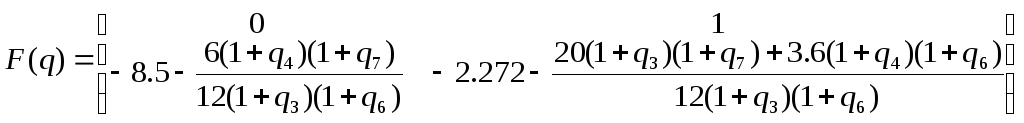
Учитывая, что , найдем :

.

Найдем :

,

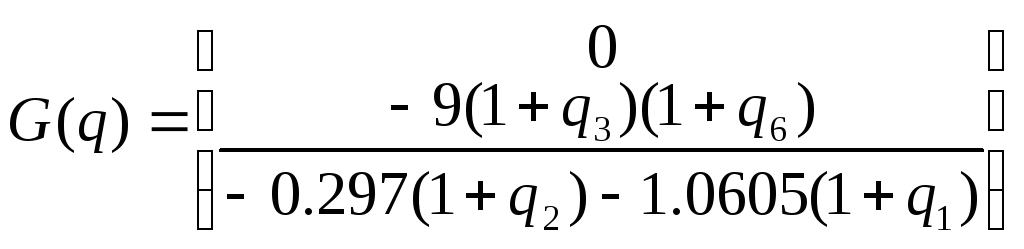
Рассчитаем передаточную функцию системы.

Переходная функция такой системы представлена на рисунке 3.1

1

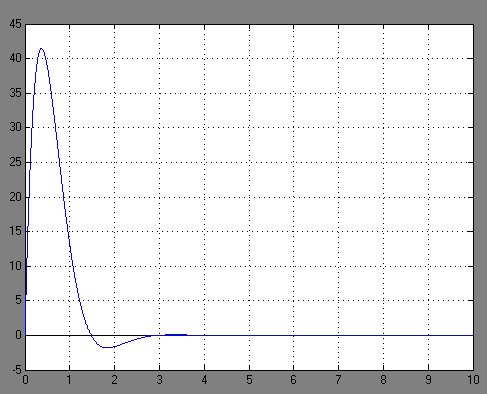
Рисунок 3.1 – Переходная функция СУ

Определим по графику на рисунке 3.1 установившееся значение: y_у= 30.3.

Построение семейства моделей траекторной чувствительности:

где , ,

,

,

,

.

Получим:

: , , ,

: , , ,

: , , ,

: , , ,

: , , ,

: , , .

Формирование семейства агрегированных систем:

где , , , .

Получим:

: , , ,

: , , ,

: , ,,

: , , ,

: , , ,

: , , .

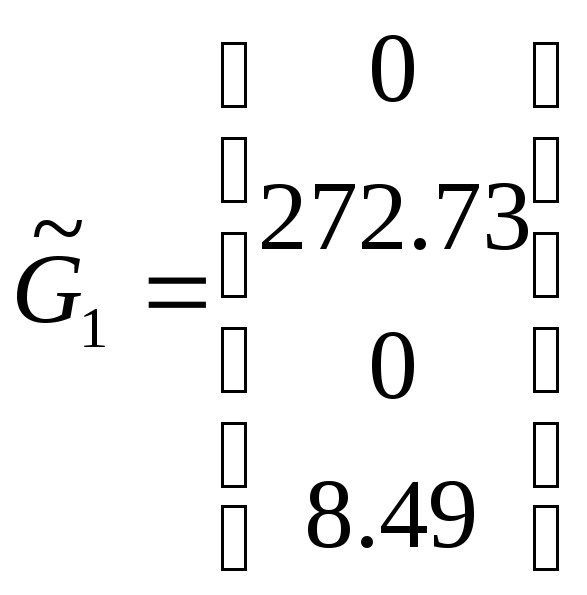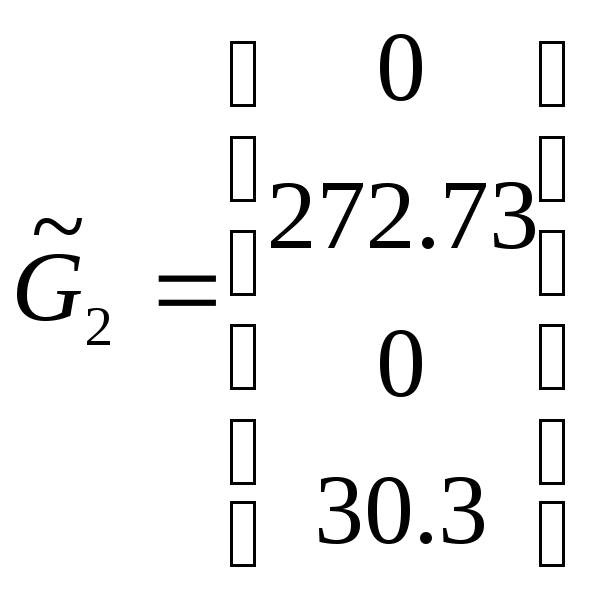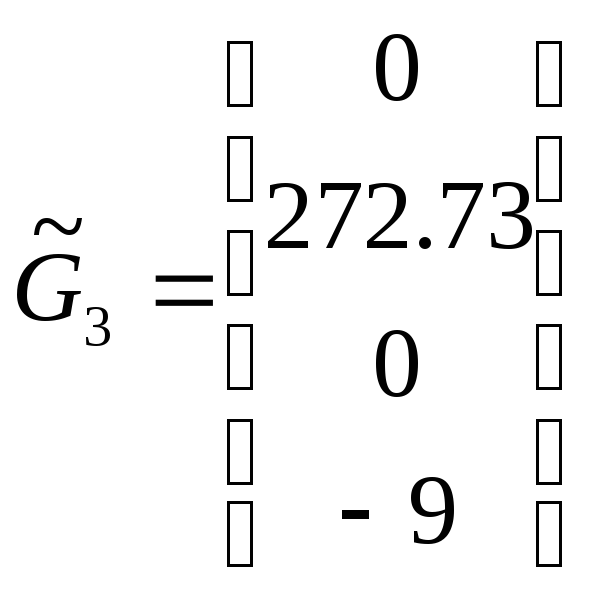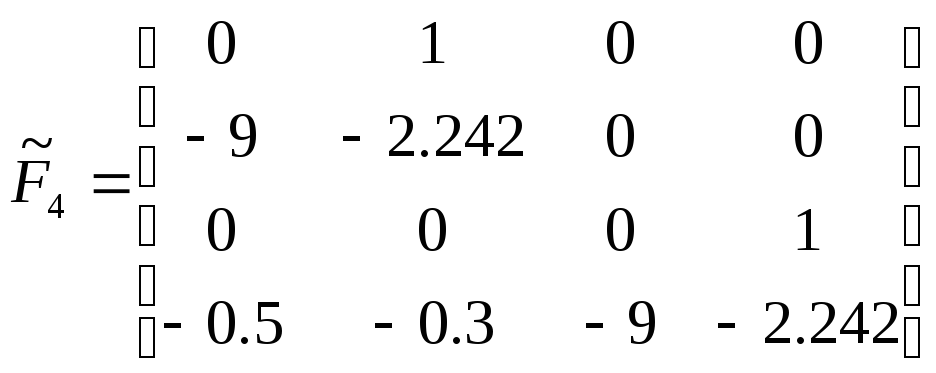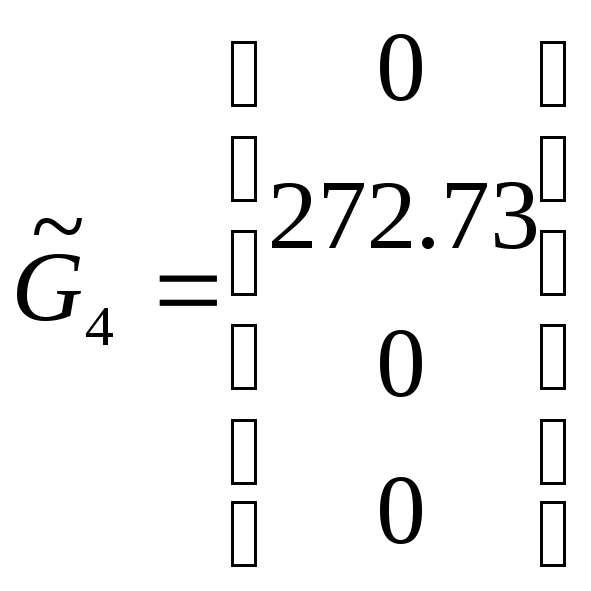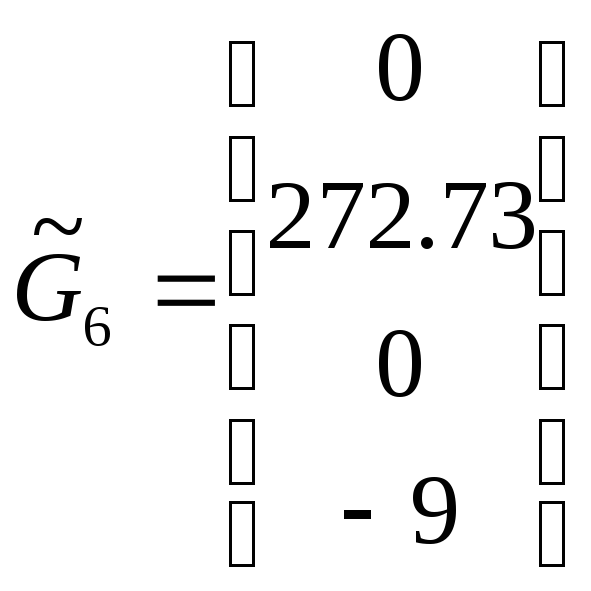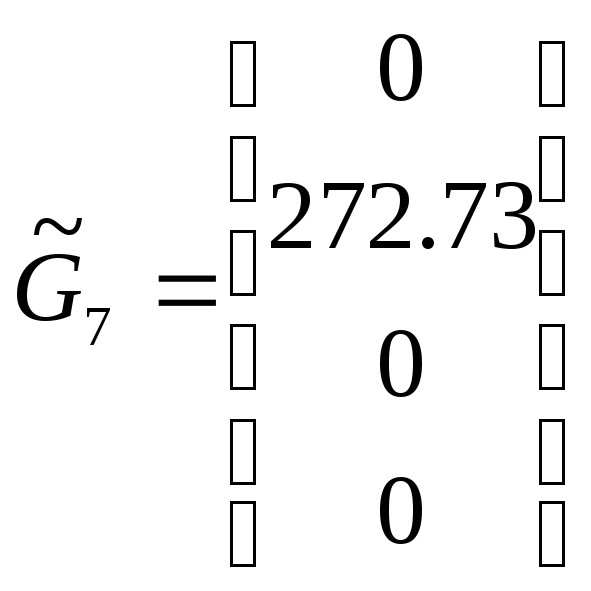На рисунке 3.2 представлена структурная схема агрегированной системы: номинального объекта управления и модели траекторной чувствительности к вариации одного из параметров.

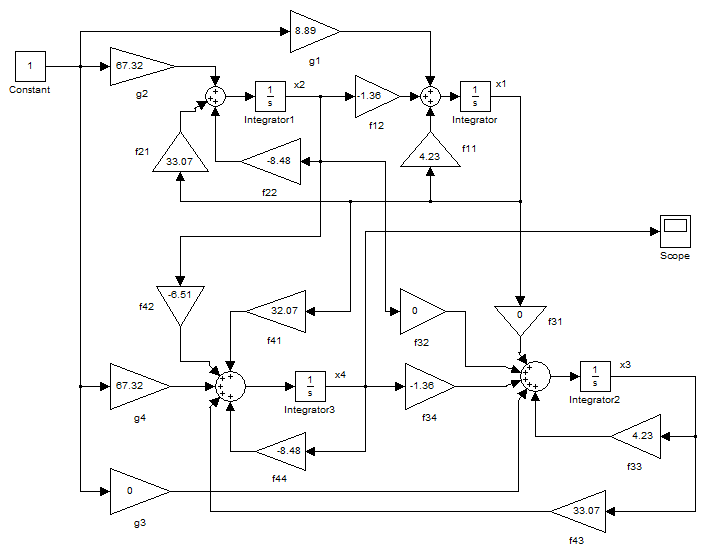
Рисунок 3.2 – Структурная схема агрегированной системы

На следующих рисунках представлены графики переходных функций номинальной системы и параметрически возмущенной, где y_н(t) – функция выхода номинальной системы, а y_в(t,q) – функция выхода возмущенной системы при и .

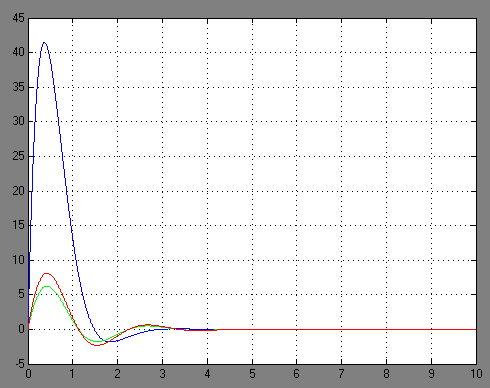
Рисунок 3.3 – Переходные функции системы при и

Определим по графику на рисунке 3.3 установившееся и максимальное значения возмущенной системы: y_у=0 и у_max=2.4; и определим в процентах разницу между значением выходной переменной номинальной системы и системы с возмущением

Рисунок 3.4 – Переходные функции системы при и .

Определим по графику на рисунке 3.4 установившееся и максимальное значения возмущенной системы: y_у=0 и у_max=7.5; и определим в процентах разницу между значением выходной переменной номинальной системы и системы с возмущением

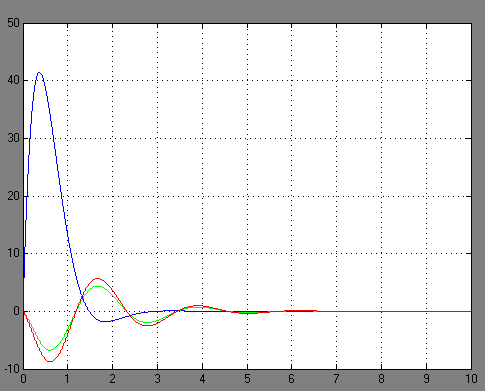
Рисунок 3.5 – Переходные функции системы при и .

Определим по графику на рисунке 3.5 установившееся и максимальное значения возмущенной системы: y_у=0 и у_max=|-8.8|; и определим в процентах разницу между значением выходной переменной номинальной системы и системы с возмущением

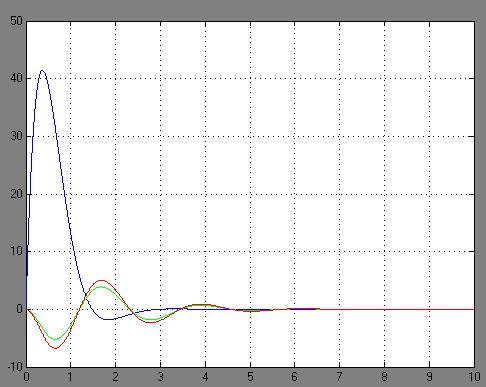
Рисунок 3.6 – Переходные функции системы при и .

Определим по графику на рисунке 3.6 установившееся и максимальное значения возмущенной системы: y_у=0 и у_max=|-6.5|; и определим в процентах разницу между значением выходной переменной номинальной системы и системы с возмущением

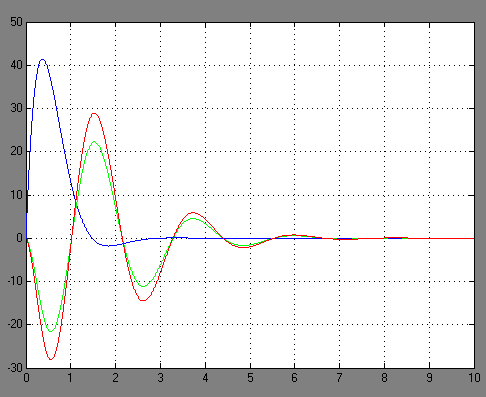
Рисунок 3.7 – Переходные функции системы при и .

Определим по графику на рисунке 3.7 установившееся и максимальное значения возмущенной системы: y_у=0 и у_max=27.5; и определим в процентах разницу между значением выходной переменной номинальной системы и системы с возмущением

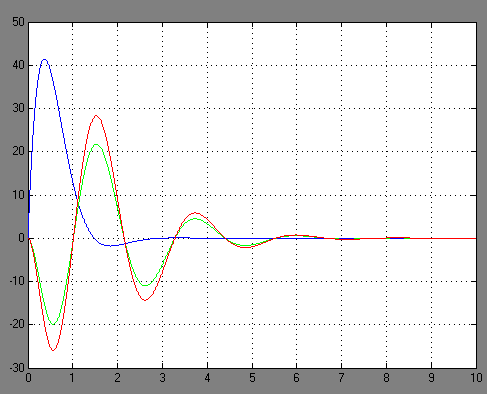
Рисунок 3.8 – Переходные функции системы при и .

Определим по графику на рисунке 3.8 установившееся и максимальное значения возмущенной системы: y_у=0 и у_max=28.8; и определим в процентах разницу между значением выходной переменной номинальной системы и системы с возмущением

Выделим доминирующие параметры по степени их влияния на величину перерегулирования и установившегося значения переходного процесса, и для этого сведем полученные результаты в таблицу 3.1.

Таблица 3.1

Вариации Параметры	q1	q2	q3	q4	q6	q7
	5.7%	17.7%	20.8%	15.4%	66.7%	67.4%

Анализируя представленные в таблице 3.1 данные, параметры по степени влияния на качество процессов следует проранжировать следующим образом:

Вывод: наибольшее влияние на показатели качества системы оказывают вариации шестого и седьмого параметров.