
- •Содержание
- •1.Введение
- •2. Проектирование логической функции
- •2.1Проектирование логической функции с использованием логических интегральных микросхем
- •2.1.1Минимизация логической функции
- •2.1.2 Проектирование логической функции с использованием любых микросхем серии к155
- •2.1.3 Проектирование логической функции с использованием микросхем к155ла3
- •Печатная плата
- •2.2 Проектирование логической функции с использованием дешифратора к155ид3
- •2.3Проектирование логической функции с использованием мультиплексора к155кп7
- •3. Проектирование делителя частоты на микросхемах к155ие7
- •3.1 Методика проектирования на микросхемах серии к155ие7
- •3.2 Проектирование делителя частоты на микросхемах к155ие6
- •3.3 Методика проектирования на микросхемах серии к155ие6
- •Проектирование системы управления по циклограмме
2.1Проектирование логической функции с использованием логических интегральных микросхем
Интегральная микросхема – микроэлектронное устройство , электронная схема произвольной сложности , изготовленная на полупроводниковом кристалле (пленке) и помещённая в неразборный корпус или без такового , в случае вхождения в состав микросборки . Для проектирования логической функции необходимо составить таблицу истинности для данной функции . Затем нужно выписать уравнение функции , соответствующее таблице истинности и посмотреть , сколько интегральных микросхем понадобится для реализации этой функции . Самые распространенные логические элементы , которые широко используются радиолюбителями – И ( & ) , ИЛИ , НЕ позволяют реализовать любую сколь угодно сложную логическую функцию .
Определения:
1) Инвертор – Логическое отрицание (инверсия) унарная операция над суждениями, результатом которой является суждение (в известном смысле) «противоположное» исходному.
2) Конъюктор – Конъюнкция - логическая операция, по своему применению максимально приближённая к союзу "и". Синонимы: логи́ческое "И", логи́ческое умноже́ние, иногда просто "И".
3) Дизъюнктор – Дизъю́нкция -, логи́ческое сложе́ние, логи́ческое ИЛИ, включа́ющее ИЛИ; иногда просто ИЛИ — логическая операция, по своему применению максимально приближённая к союзу «или» в смысле «или то, или это, или оба сразу»
Для
получения функции (1)
мы рассматривали только те значения
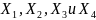 при
которых выходной сигнал F
был равен 1.
при
которых выходной сигнал F
был равен 1.
Далее мы смотрим непосредственно на значения самих сигналов X в слечае если их значени равно 1 мы записывали их в первоначальном виде, если же сигнал равен 0 над ним следует поставить знак инверсии.
2.1.1Минимизация логической функции
Преобразование логических функций с целью упрощения их аналитического представления называются минимизацией.
Минимизацию логической функции можно проводить двумя методами: аналитическим и графическим. Аналитический метод весьма трудоемок, графический – наиболее нагляден и прост в усвоении.
Минимизация по картам Карно. Составляется матрица в виде прямоугольника, состоящая из квадратов. Каждый из квадратов отображает набор переменных, отличный от других. Количество клеток в матрице равно 2n, где n – число переменных.
1 этап минимизации – выделение из общего числа клеток матрицы подкубов – объединений клеток с одинаковым значением выхода. При выделении подкубов руководствуются след. правилами:
1) Клетка матрицы с один. значением выхода должна быть включена хотя бы в один подкуб (Число подкубов может равняться 2n следовательно один, два, четыре, восемь и шестнадцать).
2) Подкуб должен объединять как можно большее число клеток матрицы.
3) Одна и та же клетка матрицы может быть включена в разные подкубы.
4) размеры матрицы подкубов могут быть увеличены за счет включения в них Х.
5)Число подкубов должно быть минимальным.
2 этап – полученные по всем подкубам произведения суммируются, образуя структурную формулу.
Составим Карту Карно для данной функции :
X2 X1
X3X4 |
00 |
01 |
11 |
10 |
00 |
0
X |
1
1 |
3
1 |
2
0 |
01 |
4
X
|
5
|
7
1 |
1 |
11 |
12
1 |
13
0 |
15
1 |
14
0 |
10 |
8
X |
9
0 |
11
0 |
10
0 |
Рис. 1 Карта Карно.
Составим уравнение для данной функции:
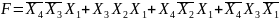 (2)
(2)



 0
0 6
6