13. Комплексные числа. Комплексная плоскость. Способы задания комплексных чисел. Операции над ними. Формула Муавра. Понятие функции комплексного переменного. Формулы Эйлера.
Комплексным числом называется число Z вида: Z = (x, y) = x+iy, где x, y – действительные числа, а i – мнимая единица. x = Re Z, y = Im Z.
Запись x+iy является алгебраической формой записи комплексного числа.
Число x-iy называется сопряженным к числу x+iy.
Кроме алгебраического задания комплексного числа, существует так же тригонометрический способ задания: Z = p(cosφ + isinφ), где p – модуль числа Z (p = корень[x2+y2]), φ (или arg Z) – угол вектора комплексного числа по отношению к оси OX.
Операции:
Z1 + Z2 = (x1+x2, y1+y2) → (r1cosφ1+r2cosφ2) + i(r1sinφ1+r2sinφ2).
Z1 * Z2 = (x1x2-y1y2, x1y2+y1x2) → r1r2(cos(φ1+φ2) + isin(φ1+φ2)).
Z1 / Z2 = ( (x1x2+y1y2)/d, (x2y1-x1y2)/d ); d = x22+y22 → r1/r2 (cos(φ1-φ2) + isin(φ1-φ2)).
Zn = (x+iy)n → (a+b)n. Zn = Sum(k от 0 до n) Cnk * xn-k(iy)k.
Формула Муавра: Zn = rn(cos nφ+isin nφ).
Формулы Эйлера:
cosφ + isinφ = eiφ Z = r(cosφ + isinφ) = reiφ = elnr * eiφ.
Комплексная плоскость это такая плоскость, точки которой интерпретируются как комплексные числа. При этом OX – действительная ось, а OY – мнимая ось.
14. Производная функции одной переменной. Геометрический и механический смысл. Правила дифференцирования (привести доказательство одного из правил). Производные элементарных функций. Производная обратной функции. Производная сложной функции (сформулировать теорему и понятие сложной и обратной функции).
Производной функции f в точке x называется предел отношения её приращения Δy в этой точке к соответствующему приращению аргумента Δx, когда аргумент стремится к нулю.
f'(x) = lim Δy/Δx при x → 0 = lim (f(x+Δx)-f(x))/Δx при x → 0
Δx = x-x0 – приращение аргумента.
Δf = f(x)-f(x0) – приращение функции, соответствующее приращению аргумента.
Геометрический смысл – тангенс угла наклона касательной к графику функции f(x) по отношению к положительному направлению оси OX.
Физический смысл – если зависимость расстояния от времени представляет собой функцию S(t), то чтобы найти скорость тела в момент времени t0, нужно найти значение производной функции S(t) в точке t0: V(t0) = S'(t0).
Правила дифференцирования:
(α1y1+α2y2)' = α1y1' + α2y2'
(y1y2)' = y1' * y2 + y1 * y2'
(y1 / y2)' = (y1' * y2 - y1 * y2') / y22
Доказательство:
П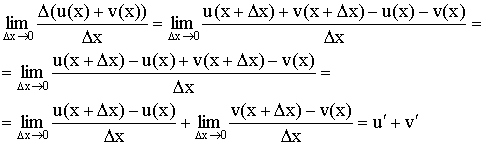
роизводные
элементарных функций:
C' = 0 (sinx)' = cosx (arcsinx)' = 1 / sqrt(1-x2)
(xn)' = nxn-1 (cosx)' = -sinx (arccosx)' = -1 / sqrt(1-x2)
(ax)' = axlna (tgx)' = 1/cos2x (arctgx)' = 1 / (1+x2)
(logax)' = 1/(xlna) (ctgx)' = -1/sin2x (arcctgx)' = -1 / (1+x2)
Производная обратной функции.
Если функция f(x) строго возрастает, непрерывна на интервале (a, b) и имеет в точке x0 конечную производную f'(x), не равную нулю, то обратная ей функция f-1(y) = g(y) имеет производную в соответствующей точке, определяемую равенством: g'(y) = 1/f'(x).
Производная сложной функции.
Если функция y=f(x) имеет производную в точке x0, а функция z=g(y) имеет производную в точке y0 = f(x0), то сложная функция z=F(x)=g(f(x)) имеет производную в точке x0, причём F'(x0) = g'(y0) * f'(x0).
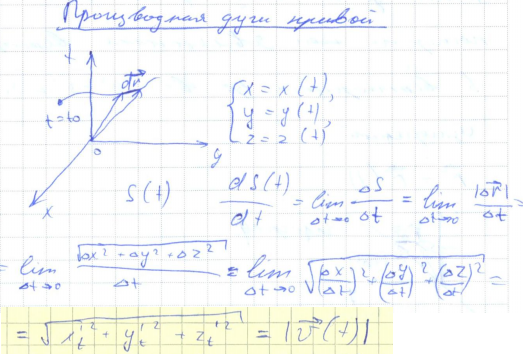
15. Производная функции одной переменной. Логарифмическое дифференцирование. Производная функции, заданной неявно. Производная функции, заданной параметрически. Производная векторной функции скалярного аргумента. Годограф. Производная длины дуги.
Производной функции f в точке x называется предел отношения её приращения Δy в этой точке к соответствующему приращению аргумента Δx, когда аргумент стремится к нулю.
f'(x) = lim Δy/Δx при x → 0 = lim (f(x+Δx)-f(x))/Δx при x → 0
Δx = x-x0 – приращение аргумента.
Δf = f(x)-f(x0) – приращение функции, соответствующее приращению аргумента.
Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него.
f'(x) = f(x) * ln(f(x))'
Производная функции, заданной неявно.
F(x, y) – неявная функция. Для дифференцирования неявной функции нужно считать, что y – сложная функция, зависящая от x.
F(x, y(x)) = 0.
Производная функции, заданной параметрически.
{ x=f(t), y=g(t) }
Если функции f(t) и g(t) дифференцируемы в точке t0, кроме того f(t) непрерывна и строго монотонна в окрестности этой точки, и её производная не равна нулю, то функция y = g(t(x)) дифференцируема в точке x0 = x(t0), причём y'(x) = yt' * tx' = yt' / xt'.
Производная векторной функции скалярного аргумента.
Векторная функция это функция, значения которой являются векторами в векторном пространстве двух, трёх и более измерений.
r = r(t).
Предел функции r(t) в точке t0 это вектор r0, для которого выполняется следующее соотношение:
lim |r(t)-r0| = 0 при t → t0.
Годограф.
Геометрическое место концов изменяющегося со временем вектора, значения которого в разные моменты времени отложены от общего начала О.
Производная длины дуги.
