2. Геометрический метод решения задач линейного программирования
Геометрический метод применяется для решения задач, когда в системе ограничений число переменных 2 или n, где n > m на 2, или n – m = 2 (n – число переменных, m – число уравнений).
Сущность геометрического метода определим при решении задачи оптимизации объема производства.
F=2x1+3x2 → max.
Решение задачи геометрическим методом.
Построим графики прямых линий.
1.Уравнение
x1+3x2=18
x1 |
0 |
6 |
x2 |
6 |
4 |
При x1=0, x2=0; тогда 0 + 3 • 0 < 18. Множество решений неравенства лежит ниже прямой (1).
2.Уравнение
2x1+x2=16
x1 |
8 |
4 |
x2 |
0 |
8 |
При (0;0), тогда 2 • 0 + 0 < 16. Множество решений лежит левее прямой (2)
3. Уравнение
x2 = 5
4. Уравнение
3x1 = 21
x1 = 7
Т.к. xi ≥ 0 , то область решения находится в 1 квадранте
Решение задачи возможно в точках A, B, C, D, E. Найдем значение x1 и x2 в каждой из точек.
1. А (0;5)
2. D (7;0)
3. Для нахождения координат точки В решим систему уравнений прямых (1) и (2) на пересечении которых находится точка В.
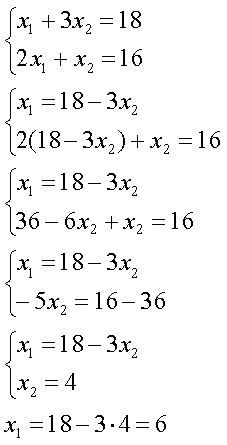
Точка В имеет координаты (6;4).
4. Аналогично найдем координаты точки С.
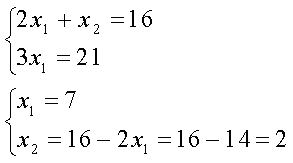
Точка С имеет координаты (7;2).
5. Найдем координаты точки Е
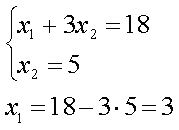
Точка Е имеет координаты (3;5).
6. Функция, определяющая критерий оптимальности, имеет вид:
F=2x1+3x2
Определим значение функции
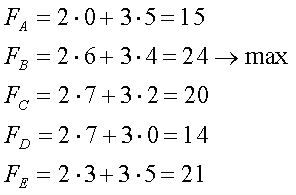
Ответ: оптимальный объем производства продукции А – 6 единиц, продукции В – 4 единицы. Тогда максимальный объем прибыли составит 24 единицы.
Определить оптимальное решение можно и не находив значение функции F во всех возможных точках решения. Для этого строят прямую линию по уравнению функции F. Например: пусть F=0, тогда F=2x1+3x2 =0 проходит через начало координат. Пусть F=6, тогда 2x1+3x2 =6
x1 |
0 |
3 |
x2 |
2 |
0 |
Построим прямую линию по выбранным координатам.
Параллельно смещая прямую линию функции до точек - возможных решений, мы определим оптимальное решение в точке, максимально удаленной от линии F=0. Далее находим координаты данной точки, решая систему уравнений, на пересечении которых она находится.
При решении экономических задач геометрическим методом важно помнить:
1. Не всегда возможно определить конечное оптимальное решение.
2. Возможны случаи, когда условие задачи противоречивы, тогда система ограничений не дает решения, т.е. оптимальное решение найдено не может быть.
3. Метод прост и нагляден. Однако, не лишен погрешностей при построении графиков.
4. Не всегда экономические задачи можно решить данным методом (например, без дополнительных расчетов нельзя определить остатки материальных ресурсов на складе, в производстве; избыток чего либо и др.)
5. Принимают в случае двух переменных. Для любого другого количества переменных используют аналитические методы.