Тема 7. Оптимизация процессов управления запасов
Занятие 6
Основная модель управления запасами. Методика определения оптимального размера, интервала, стоимости запаса.
Модификация основной модели, условия модификации. Методика принятия оптимального экономического решения.
Решение задач средствами MS Excel
Модель управления запасами
Годовой спрос производственного предприятия на комплектующие составляет 60 тысяч единиц. Стоимость размещения одного заказа оценивается специалистами предприятия в 25 у.е., а стоимость хранения составляет 24% от его закупочной цены, которая равна 8 у.е.
Перенесем условие задачи в пакет MS Excel, как показано на рисунке 36.
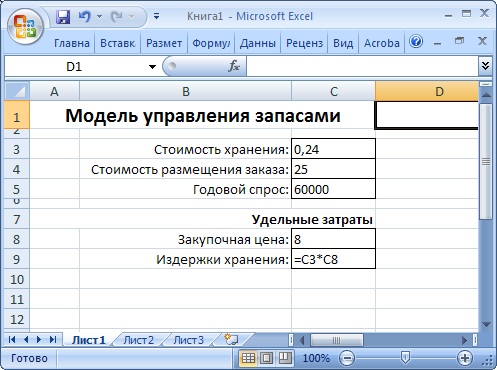
Рисунок 36. Условие задачи (в режиме проверки формул)
Для нахождения оптимального решения составим математическую модель управления запасами (рисунок 37). Данная модель является нелинейной, поскольку q входит в качестве знаменателя в формулу целевой функции, описывающей суммарные годовые затраты.
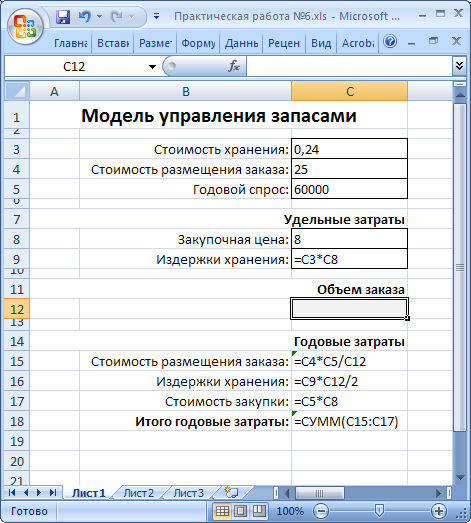
Рисунок 37. Математическая модель управления запасами
Формулы
в ячейках С16:С17 описывают издержки
размещения запасов и издержки хранения
запасов. Поскольку стоимость закупки
постоянна и не зависит от q
(стоимость закупки = закупочная цена
годовой спрос), она не используется для
вычисления оптимального значения q.
Она включена в модель для полноты
определения суммарных годовых затрат.
Ограничение, требующее, чтобы в течение
года был размещен хотя бы один заказ
будет включено в модель для того, чтобы
средство «Поиск решения» не проверяло
вариант q=0,
что является вариантом, когда деятельность
не ведется и приведет к ошибке деления
на 0 в формуле издержек размещения
заказов. Для нахождения оптимального
решения воспользуемся инструментом
«Поиск решения», настройки которого
изображены на рисунке 38.
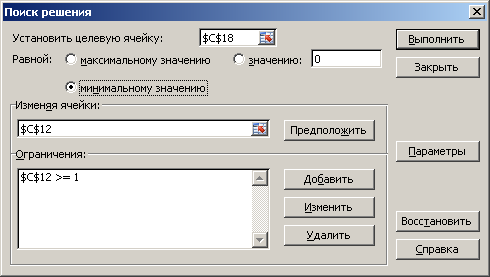
Рисунок 38. Настройки инструмента «Поиск решения»
Результат выполнения вычислений приведен на рисунке 39.
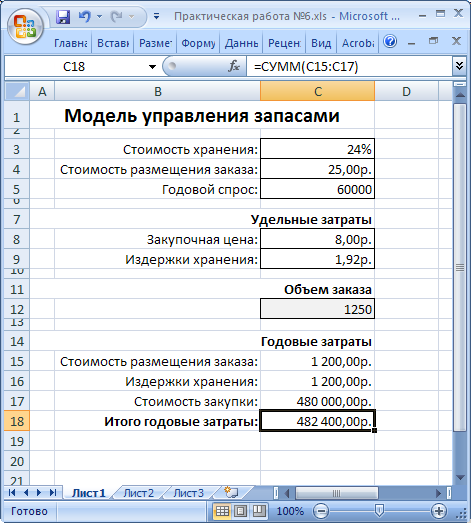
Рисунок 39. Результат решения задачи
Модель управления запасами при наличии оптовых скидок
Предположим, что для рассмотренной нами задачи добавляется новое условие – скидка 0,10 у.е. при одновременном заказе не менее чем 5000 тысяч единиц комплектующих. Больший размер заказов приведет к уменьшению количества заказов и соответственно годовых издержек размещения заказов. Но при этом больший размер заказа приводит к увеличению среднего уровня запасов и повышению издержек хранения. Очевидно, что предприятие хотело бы минимизировать совокупные годовые затраты и в такой ситуации не ясно, будет ли выгодна оптовая скидка. Чтобы определить, какое решение является оптимальным, необходимо вычислить совокупные затраты для случаев, когда заказываемое количество комплектующих меньше границы предоставления скидки и когда оно равно или превышает ее.
Модифицируем разработанную нами модель, добавив туда расчет для возможного предоставления скидки, как это показано на рисунке 40.
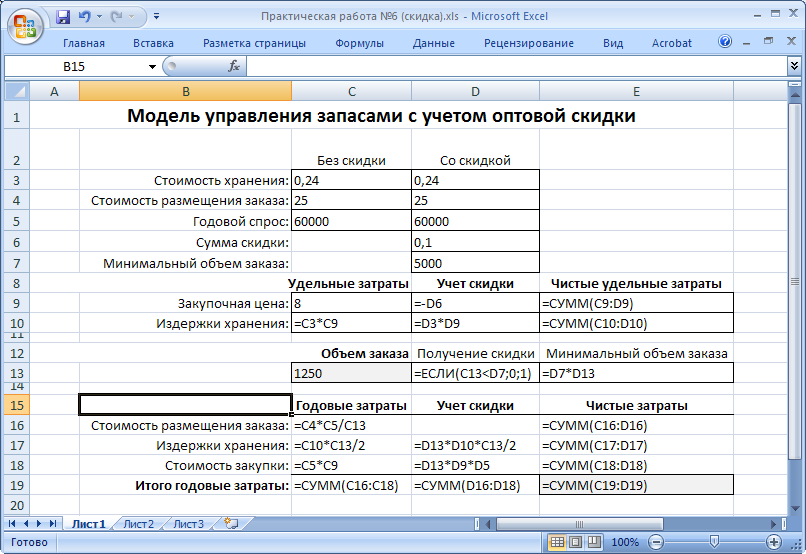
Рисунок 40. Модель управления запасами с учетом оптовой скидки
В отличие от предложенного выше подхода/ модель в Excel сформирована так, что годовые затраты записываются как годовые затраты при отсутствии скидки в ячейках С16:С19 минус поправка на сумму скидки, если такая имеет место. Таким образом, если скидка получена, то слагаемые годовых затрат «Издержки хранения» и «Стоимость закупки» вносятся соответствующие поправки, отражающие сумму скидки. Эти затраты объединяются в «Совокупные чистые затраты» в ячейках Е16:Е19. Такой подход позволяет трактовать получение скидки как двоичную переменную решения (ячейка D13). Формула в ячейке D13 записана в виде логического выражения =ЕСЛИ(C13<D7;0;1). Это означает, что если объем заказа меньше чем порог предоставления скидки, то в данную ячейку ставится значение «0», если больше либо равно порогу, то ставится значение «1». Смоделируем 3 случая: объем заказа меньше порога предоставления скидки (рисунок 41), равен порогу (рисунок 42), больше порога (рисунок 43).
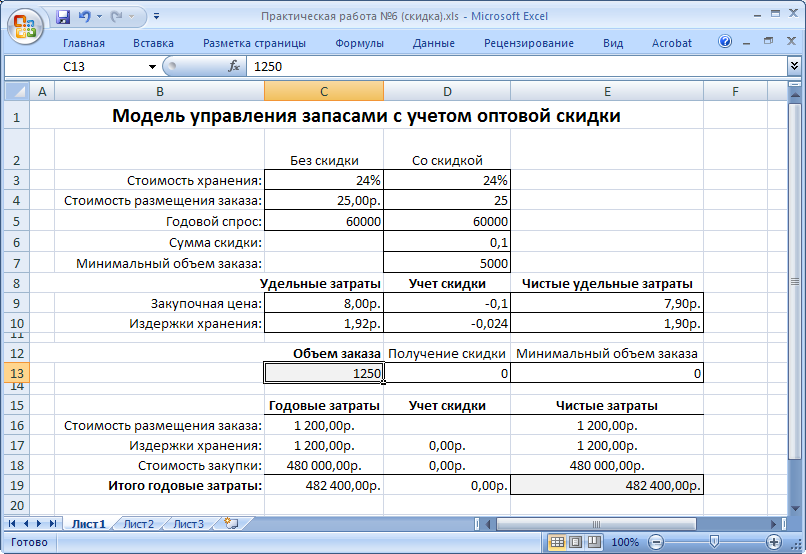
Рисунок 41. Объем заказа меньше порога предоставления скидки
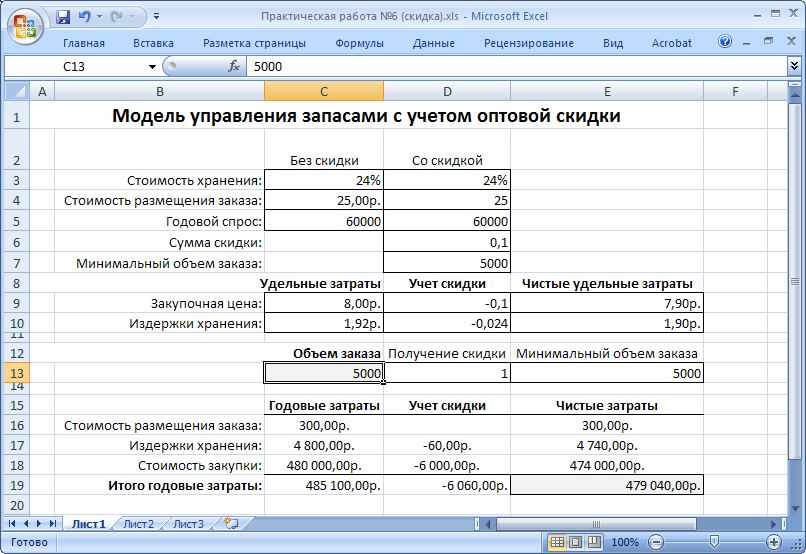
Рисунок 42. Объем заказа меньше порога предоставления скидки
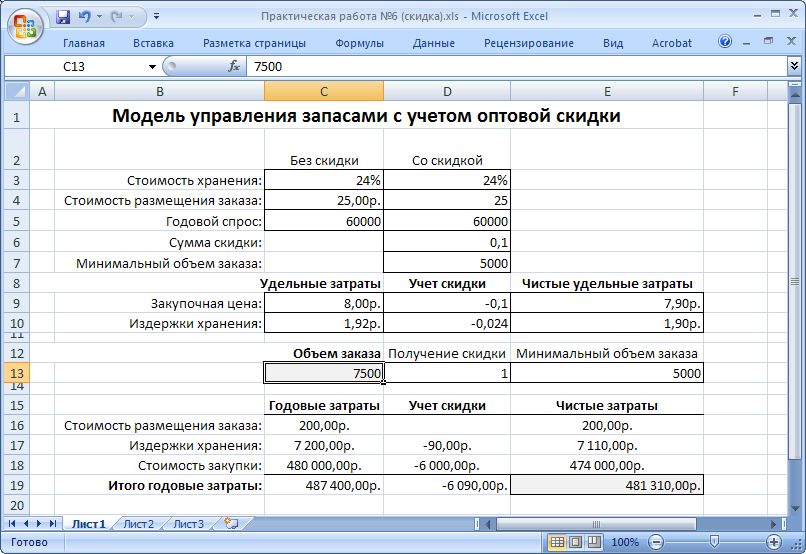
Рисунок 43. Объем заказа больше порога предоставления скидки
Чтобы отразить в модели существование системы скидок (т.е. когда существует несколько пороговых значений размера заказа с каждым из которых связаны «поправки» к общим затратам) необходимо ввести дополнительные двоичные переменные, и внести соответствующие изменения в формулы. В рассматриваемом примере мы видим, что если воспользоваться возможностью заказа бОльшего количества комплектующих со скидкой, то это позволит сэкономить более 3-х тысяч у.е. в год (для заказа в 5000 тысяч штук экономия составит 482400-479040=3360 у.е.).
Производство и управление запасами
Модель определения оптимального размера партии продукции приведена на рисунке 44.
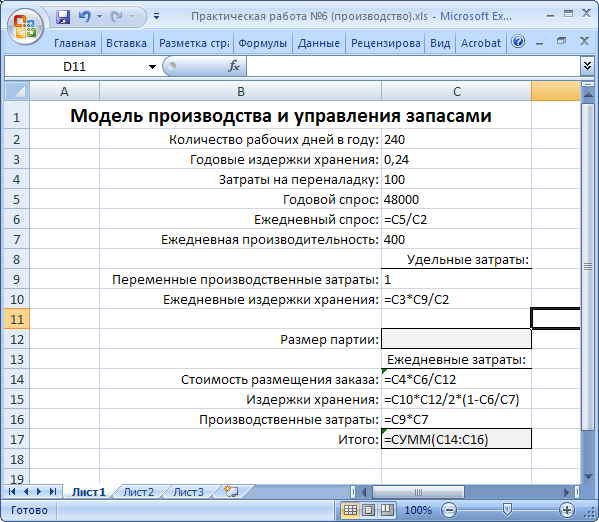
Рисунок 44. Модель определения оптимального размера партии продукции
Воспользуемся инструментом «Поиск решения», определив для него следующие настройки:
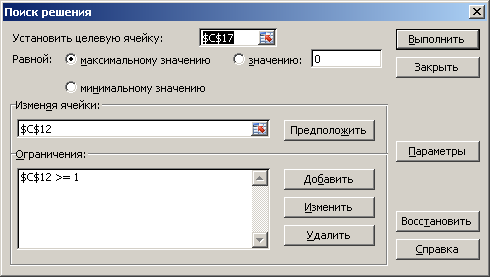
Найденное оптимальное решение приведено на рисунке 45.
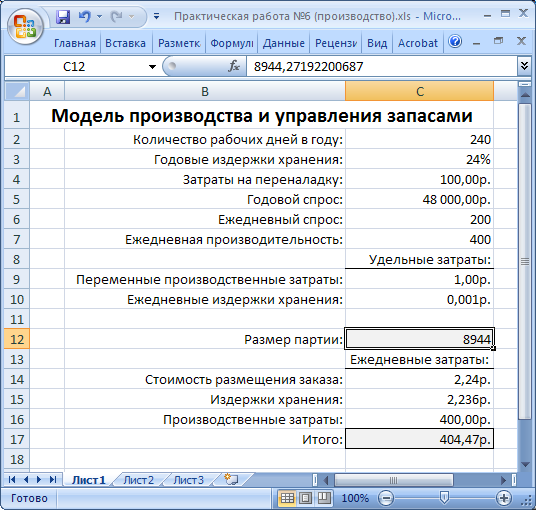
Рисунок 45. Оптимальный размер партии продукции
Задача 7.1.
Общество с ограниченной ответственностью занимается продажей сложной бытовой техники. Одним из видов продукции являются электрочайники. Спрос на них равномерный составляет 25 единиц в неделю. Фирма закупает электрочайники по цене 9 у.е. за единицу. Стоимость оформления договора на один заказ составляет 15 у.е., a издержки хранения 0,5 у.е. за единицу среднего размера запаса в течение года плюс 15% среднегодовой стоимости запасов. В году 50 рабочих недель.
Определить:
Оптимальный размер запаса.
В настоящее время сложился опыт заказа партиями в 300 единиц продукции. Какой будет величина экономии, если заказы будут поступать в соответствии с оптимальным размером заказа ?
Какое целесообразно принять экономическое решение в случае снижения цены подачи одного заказа до 5 у.е. ?