Задача 5.1.

Магазин может завезти в различных пропорциях товары трех типов A1, А2, А3. Предполагается, что спрос может иметь три состояния и не спрогнозирован Определить оптимальные пропорции в закупке товаров из условия максимизации средней гарантированной прибыли при следующей матрицы прибыли.

Тип товара	Спрос
	B1	B2	В3
A1	20	15	10
A2	16	12	14
А3	13	18	15

Задача 5.2.

Предприятие выпускает скоропортящуюся продукцию, которую может сразу отправить потребителю (стратегия А1), отправить на склад для хранения (стратегия А2) или подвергнуть дополнительной обработке (стратегия А3) для длительного хранения. Потребитель может приобрести продукцию немедленно (стратегия B1), в течение небольшого периода времени (стратегия B2), после длительного периода времени (стратегия B3).

В случае стратегий А2 и А3 предприятие несет дополнительные затраты на хранение и обработку продукции. Стратегия А2 характеризуется убытками из-за порчи продукции, если потребитель выберет стратегии B2 или B3.

Определить оптимальные пропорции продукции для применения стратегий А1, А2, А3, руководствуясь минимаксным критерием, т.е. получением среднего уровня убытка при следующей матрице затрат:

Bj / Ai	B1	B2	В3
A1	2	5	8
A2	7	6	10
А3	12	10	8

Тема 6. Сетевой анализ и оптимальное календарное планирование производственно-хозяйственной деятельности объектов

Занятие 5

1. Основные элементы сетевой модели.

2. Правила построения сетевых моделей.

3. Методика экономического анализа критического пути.

4. Оптимизация сроков и стоимости реализации проекта.

5. Анализ сетевых графиков в среде MS Project

6. Решение задач

Анализ сетевых графиков в среде MS Project

Рассмотрим сетевой график, приведенный на рисунке 24.

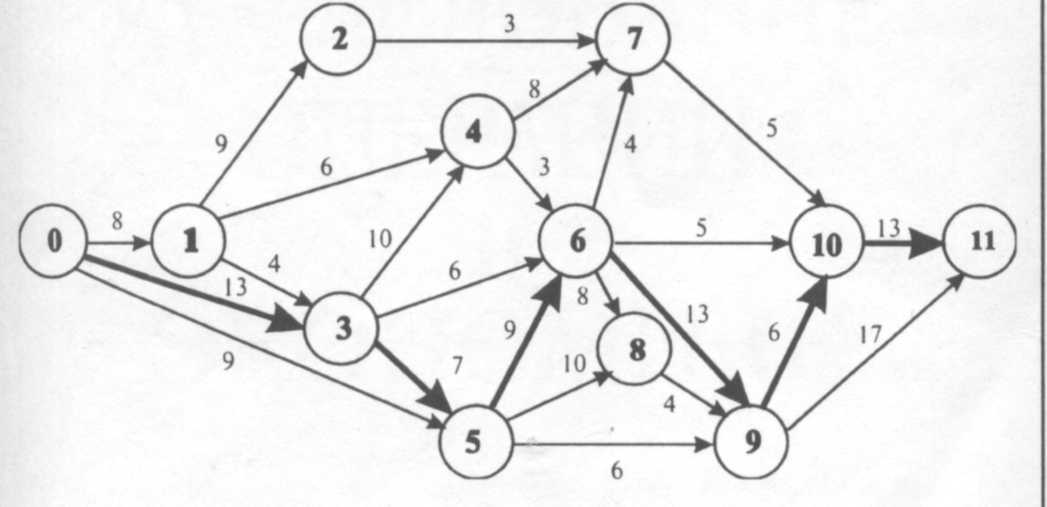
Рисунок 24. Сетевой график

В его составе можно выделить узлы – 0, 1, 2,…, 11 (назовем их «события 1» и т.д.), и работы, связывающие эти узлы – 0-1, 0-3, 0-5 и т.д. (назовем их соответственно «работа 0-1» и т.д.). Кроме того, на графике изображено количество дней, требуемых на выполнение каждой работы (например, работа 0-3 выполняется в течение 13 дней).

Для работы с календарным и сетевым планированием применяется продукт из комплекта Microsoft Office – Microsoft Project. На рисунке 25 изображено главное окно программы:

Рисунок 25. Главное окно программы

Оно разделено на две основных области – в левой части описываются задачи и их параметры, в правой – происходит визуальное отображение задач и их взаимосвязей. Задачи, вносимые в состав проекта могут иметь иерархическую структуру.

Рассмотрим на примере нашего сетевого графика. Как было обозначено в состав его входит несколько узлов (событий). Внесем эти события в левую область Microsoft Project , для этого достаточно встать мышкой на ячейку «Название задачи» и ввести с клавиатуры ее название, как показано на рисунке 26. Событие 11, являющееся завершающим событием в сетевом графике назовем «Реализация проекта».

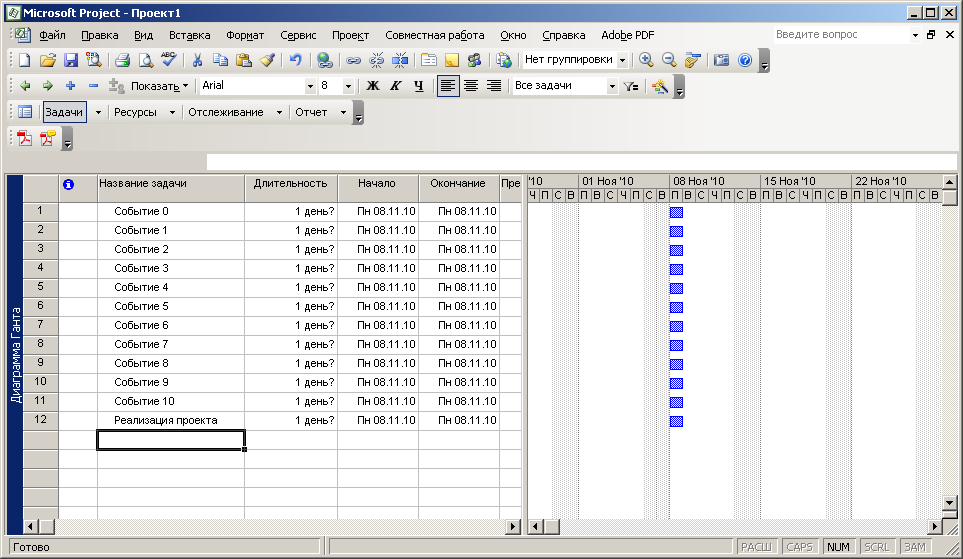
Рисунок 26. Ввод событий (узлов сетевого графика)

Обратим внимание на поле «Длительность». По умолчанию, если длительность выполнения задачи не задана, то подразумевается, что задача имеет длительность 1 день. В случае, если у задачи есть вложенные подзадачи, то тогда она считается «веховой задачей» и ее длительность равна максимальной длительности задач, в нее входящих. Мы увидим это позднее.

Из узла 0 (событие 0) нашего сетевого графика выходят 3 работы – 0-1, 0-3, 0-5. Добавим эти работы в перечень задач в левой области MS Project ниже события 0. Для этого выделив событие 1 вызовем правым кликом мыши контекстное меню и выберем пункт «Новая задача» (рисунок 27). Назовем их «Работа 0-1», «Работа 0-3», «Работа 0-5».

Рисунок 27. Добавление подзадачи

Для каждой из вновь введенных работ заполним поле «Длительность», внеся туда соответственно числа 8, 13, 9 (длительность работ согласно сетевому графику).

Обозначим, что данные работы относятся к событию 0, входят в его состав. Для этого выделим вновь введенные задачи и вызвав контекстное меню выберем пункт «На уровень ниже». Результат выполнения приведен на рисунке 28. Задача «Событие 0» стала веховой, состоящей из 3-х подзадач.

Рисунок 28. Создание иерархии задач

Аналогичным образом введем все оставшиеся задачи, учитывая, что все работы, выходящие из узла (события) обозначаем как его соответствующие подзадачи. Кроме того задача, названная «Реализация проекта» является веховой для всех событий 0-11, которые входят в нее как составные узлы. В результате мы получим иерархический список задач с указанием их длительности, представленный на рисунке 29.

Рисунок 29. Иерархический список задач

Зададим взаимосвязь между задачами, согласно сетевому графику. Мы видим, что событие 3 (узел 3 сетевого графика) не может наступить до тех пор, пока не закончатся входящие в него работы (работа 0-3, работа 1-3). Значит все работы исходящие из узла 3 не могут начаться до тех пор, пока не закончатся работы 0-3 и 1-3. Т.е. нам необходимо задать системе условие, что сроком начала работ 3-N являются сроки окончания работ M-3. Самый простой способ сделать это в пакете MS Project – в области диаграммы взять отрезок, обозначающий, например работу 0-3 и перенести его на отрезок работы, например 3-5 (рисунок 30).

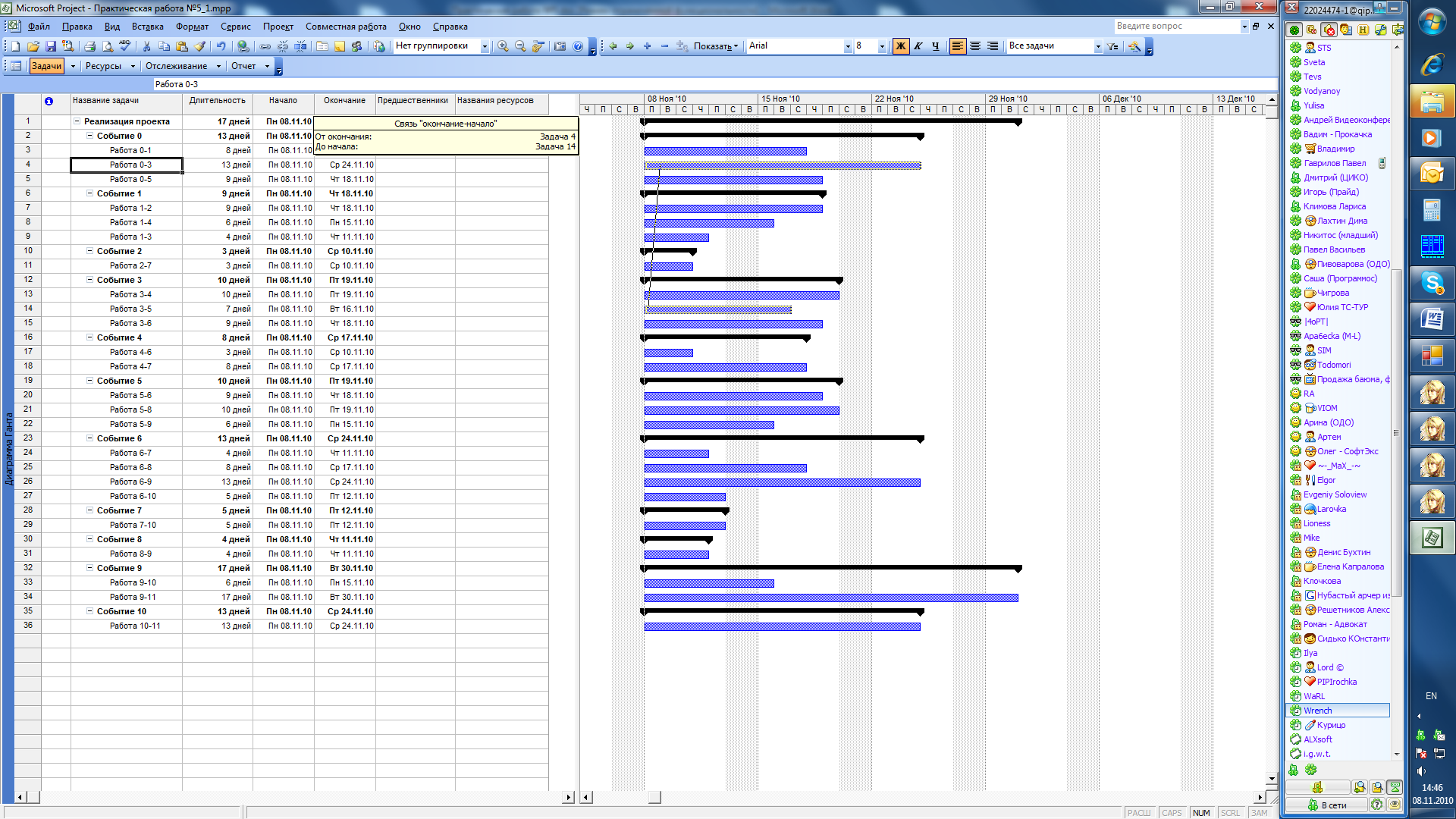
Рисунок 30. Установление взаимосвязи между сроками выполнения задач

Видим, что начало работы 3-5 сместилось в календарном плане на ту дату, когда закончилась работа 0-3. Повторим аналогичную операцию с работами 1-3 и 3-4, 3-5, 3-6. В результате мы видим, что все работы, выходящие из узла 3 (входящие в состав события 3) начинаются только после того, как закончатся все работы, в этот узел входящие (рисунок 31).

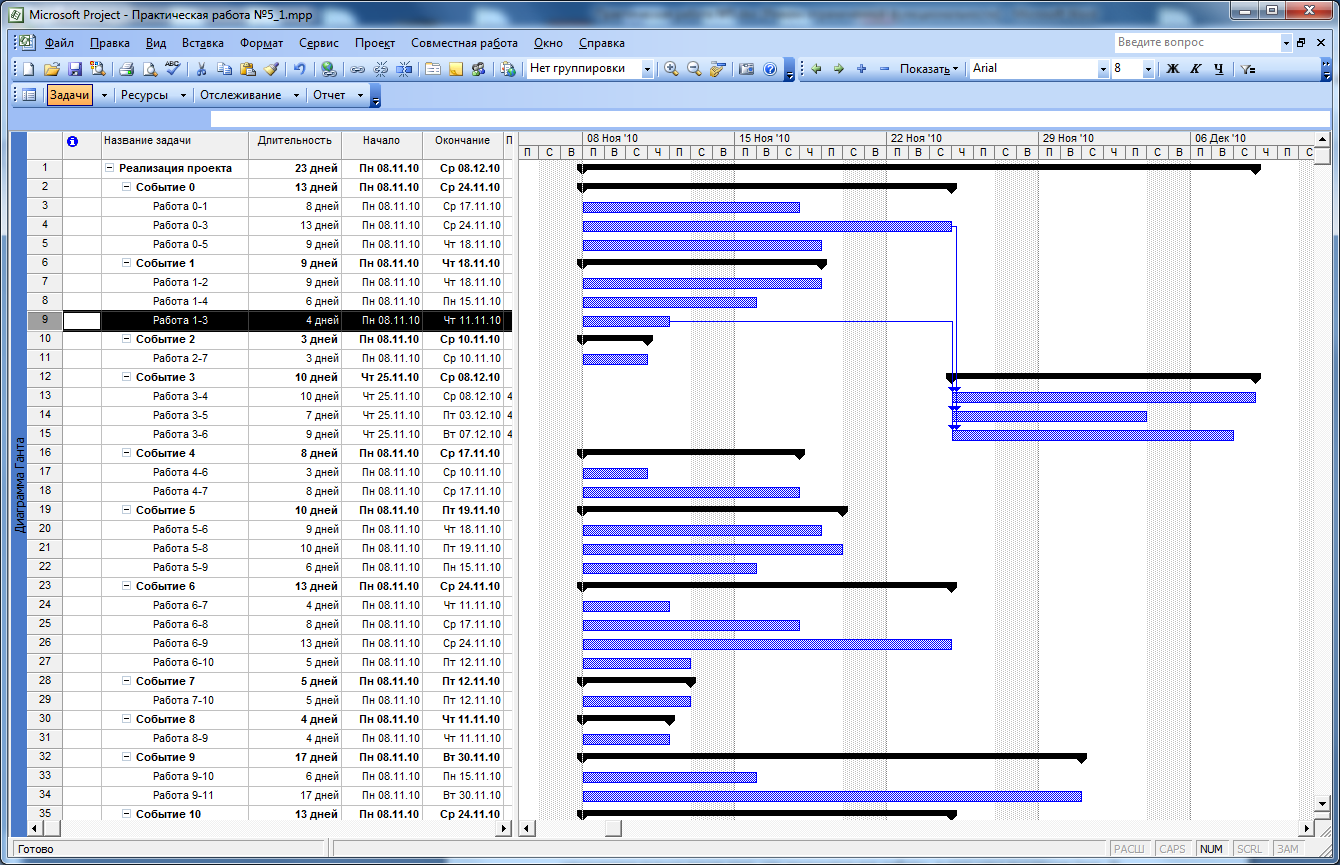
Рисунок 31. Установление взаимосвязи между сроками выполнения задач

Внимательно прорабатывая сетевой график выстроим иерархию всех работ, входящих в проект. В результате получаем диаграмму, изображенную на рисунке 32.

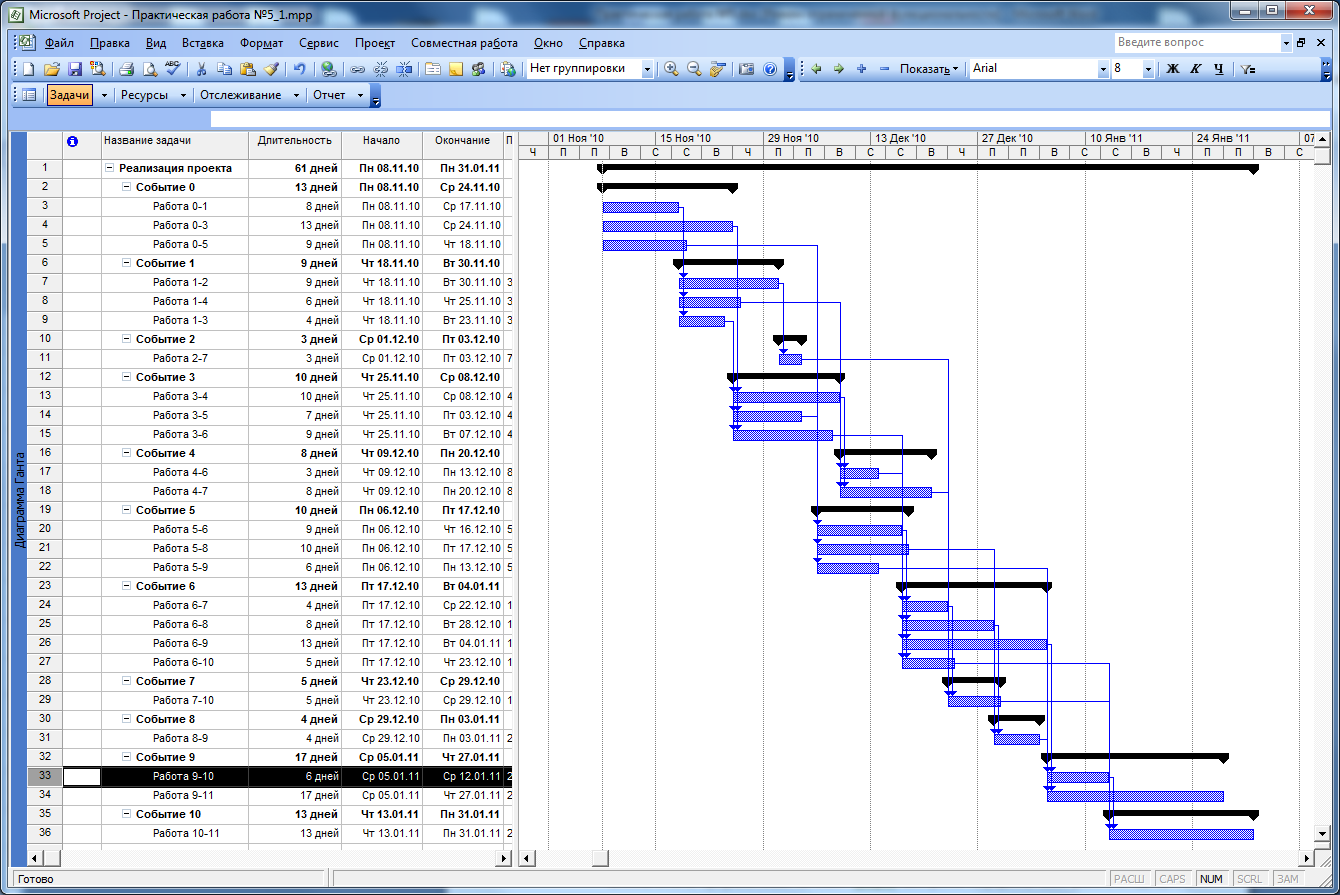
Рисунок 32.

Таким образом, мы перенесли в программу в виде линейной диаграммы (диаграммы Ганта) сетевую модель нашей задачи с учетом всех узлов, работ, их длительностей и взаимосвязей.

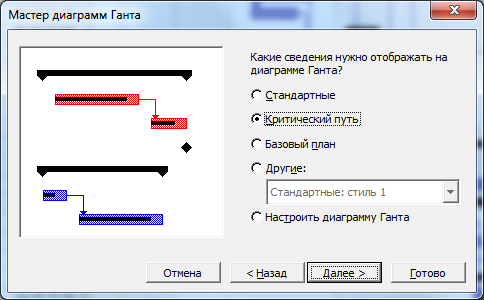
Для нахождения критического пути нашего проекта запустим мастер настройки диаграммы Ганта (Пункт меню «Формат – Настройка диаграммы Ганта»). На втором шаге мастера отметим, что на диаграмме необходимо отображать критический путь:

После применения параметров мастера на нашей диаграмме (рисунок 33) критический путь будет отмечен красным цветом. Мы видим, что он проходит через работы 0-3, 3-5, 5-6, 6-9, 9-10, 10-11.

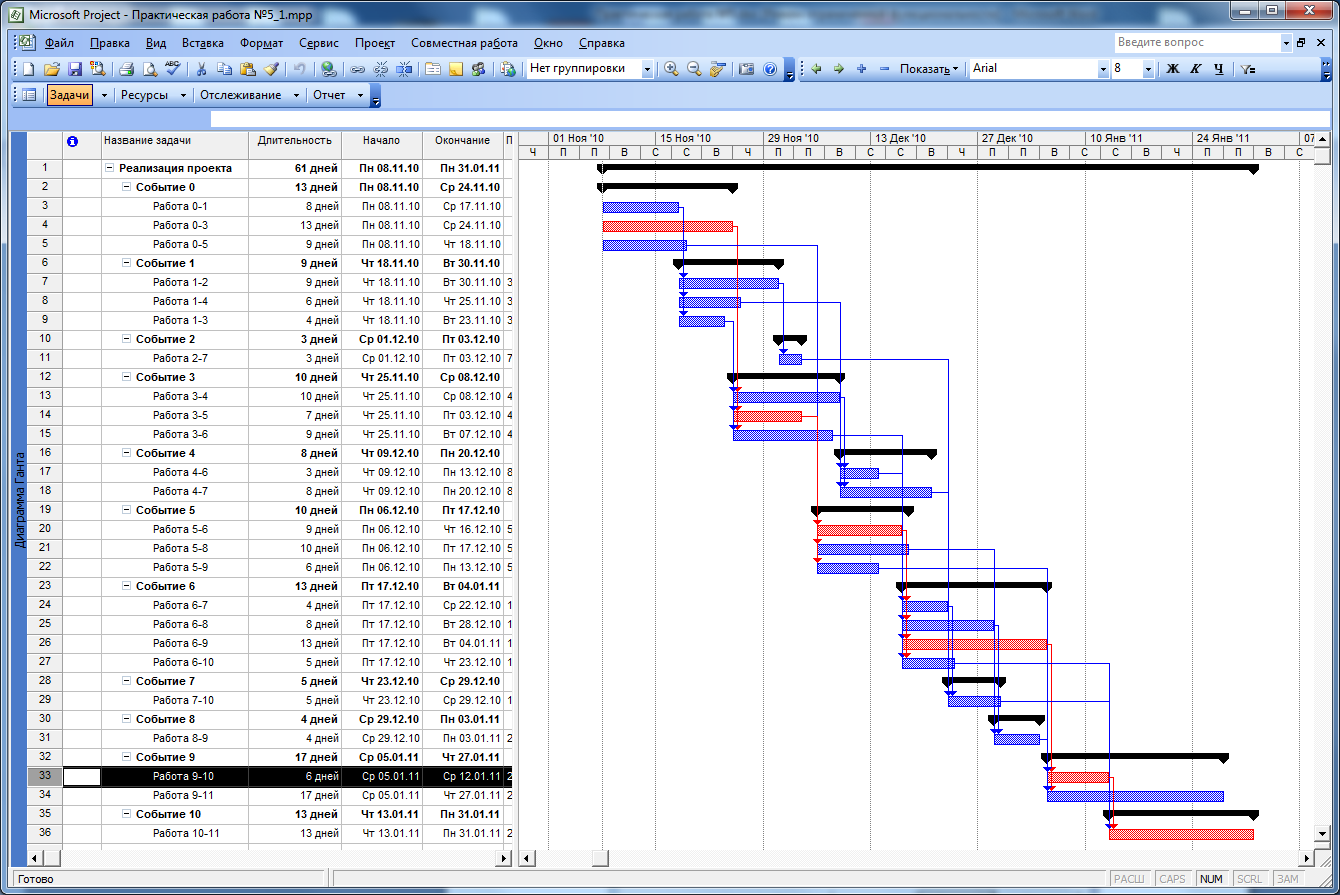
Рисунок 33. Обозначение критического пути

Теперь настроим табличную часть проекта для получения необходимых нам сведений о нашей сетевой модели. Для этого добавим в табличную часть следующие колонки (пункт меню «Вставка->Столбец»): «Раннее начало», «Раннее окончание», «Позднее начало», «Позднее окончание», «Общий временной резерв», «Свободный временной резерв», уберем столбцы «Предшественник» и «Название ресурсов». Проанализируем табличную часть проекта, приведенную на рисунке 34 и 35.

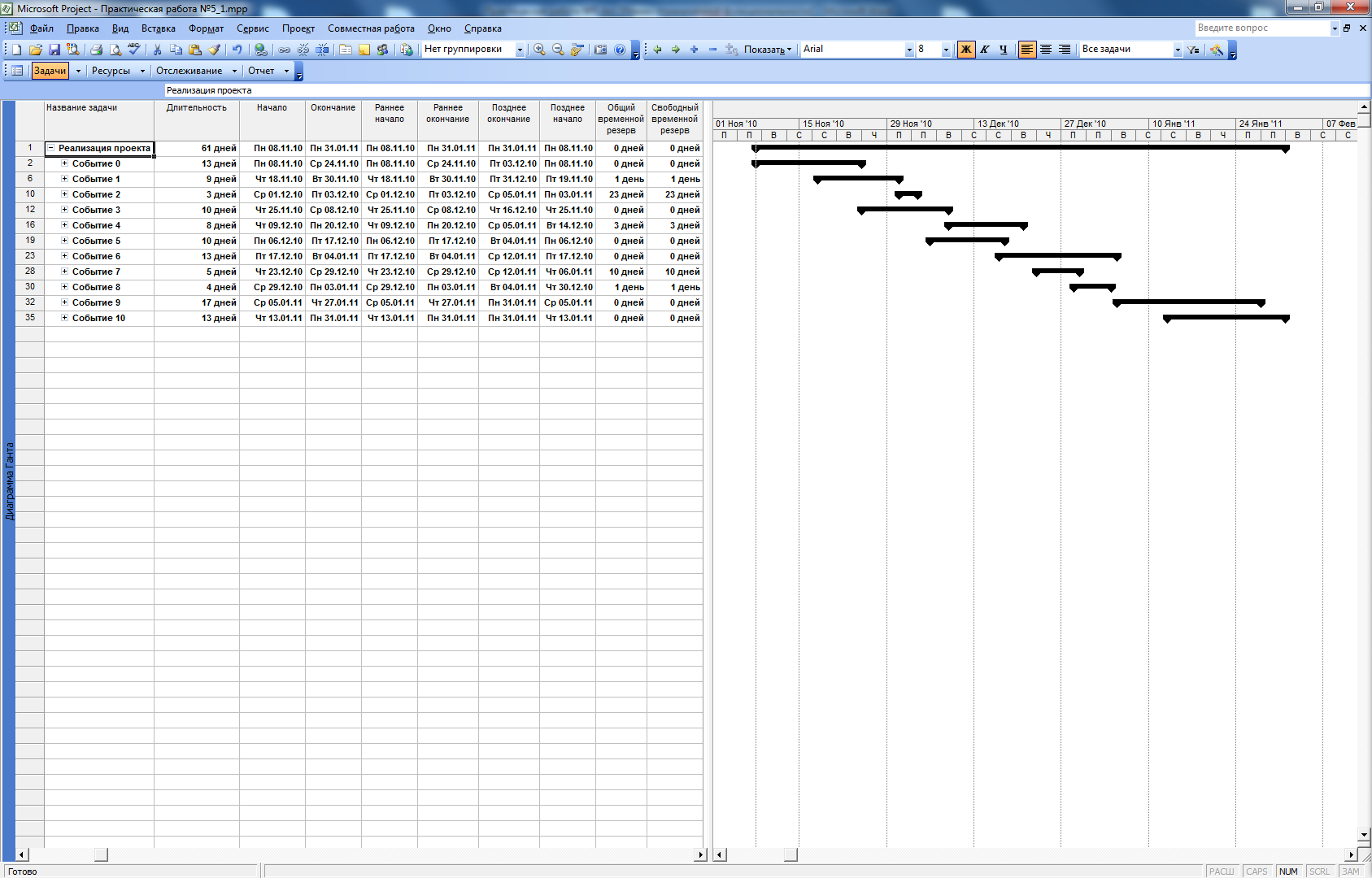
Рисунок 34. Сведения о проекте (свернутые)

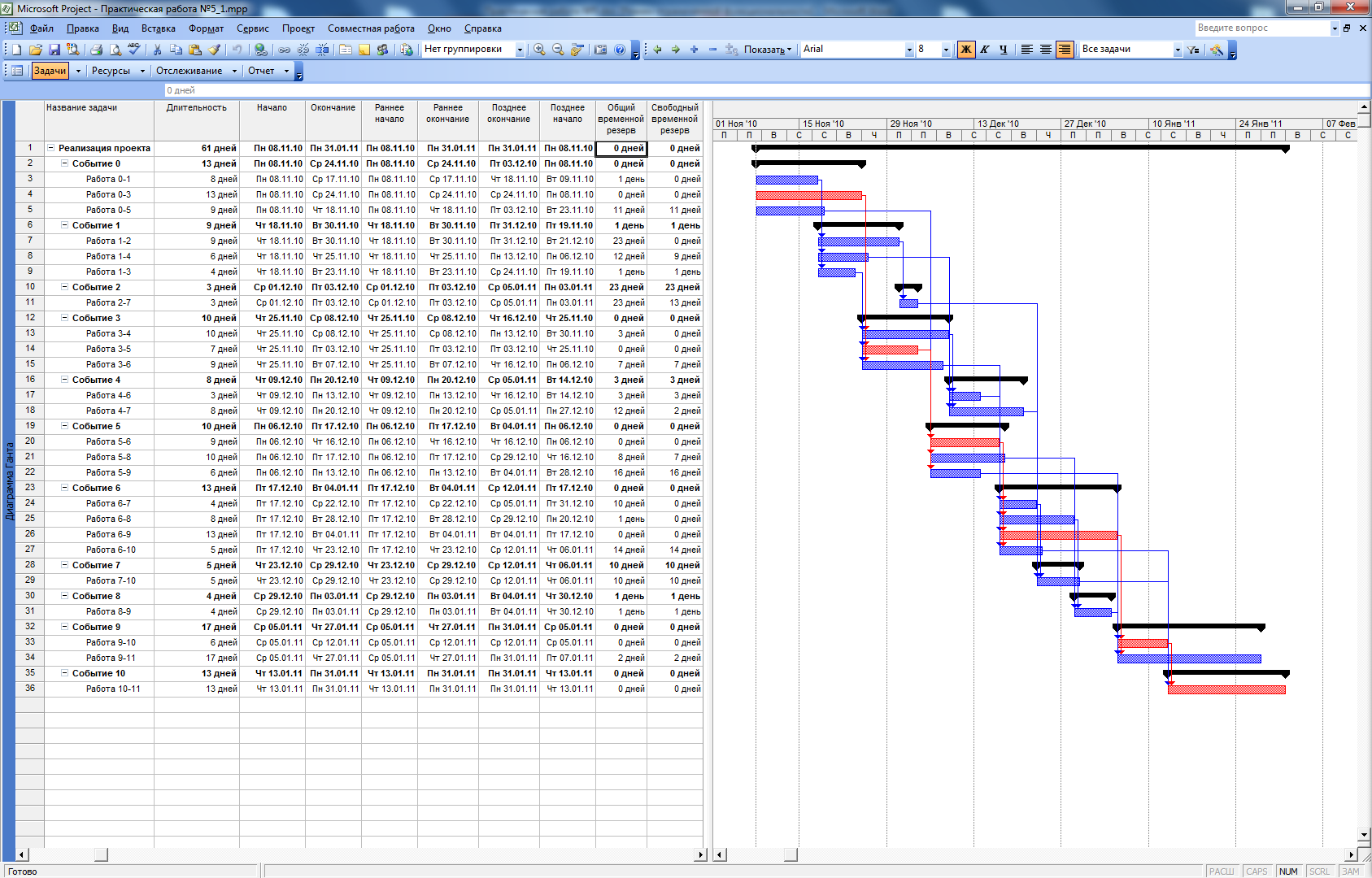
Рисунок 35. Сведения о проекте (развернутые)

Из курса лекций мы знаем, что основными параметрами, рассматриваемыми при анализе сетевых моделей являются длинна критического пути, а также временные параметры работ, к которым относятся резерв времени для каждого события, продолжительность работы, ранние и поздние сроки окончания работы, резервы времени работы.

Обратим внимание на рисунок 34:

- В поле «Длительность» для глобальной задачи «Реализация проекта», включающей в себя все остальные узлы и работы, указана длинна критического пути, составляющая 61 день;

- В поле «Общий временной резерв» содержится резерв времени R(i) для каждого события, таким образом:

Номер события	Резерв времени R(i)
0	0
1	1
2	23
3	0
4	3
5	0
6	0
7	10
8	1
9	0
10	0
11 (Реализация проекта)	0

Обратим внимание на рисунок 35:

- В полях «Раннее начало», «Раннее окончание», «Позднее начало», «Позднее окончание» содержатся сроки начала и окончания работы. Следует отметить, что поскольку одно из основных назначений пакета – это календарное планирование, то сроки начала и окончания работ формируются как конкретные даты, с учетом календаря рабочего времени (выходных дней). Такое представление отличается от изучаемого в классической теории, когда сроки начала и окончания работ выражаются в количестве дней, но гораздо удобнее в практическом применении.

- В поле «Общий временной резерв» выводится значение полного резерва времени для каждой работы R_П(I,j)

- В поле «Свободный временной резерв» значение свободного резерва времени (частный резерв времени второго вида) R_С(i,j)

Частный резерв времени первого вида R₁(I,j) легко вычисляется по формуле R₁(I,j)=R_п(I,j)-R(i), и, например, для работы 1-2 составляет R₁(1,2)=R_П(1,2)-R(1)=23-1=22

Независимый резерв времени R_Н(I,j) расчитывается по формуле R_H(I,j)=R_П(I,j)-R(i)-R(j), и, например, для работы 1-4 составляет R_Н(1,4)=R_П(1,4)-R(1)-R(4) = 12-1-3=8

Аналогичным образом находятся остальные параметры сетевого графика.