Задача 3.6.

Имеются три вида ресурсов, которые используются в производстве трех видов продукции А, Б и В

Ресурс	Норма расхода на единицу продукции
	А	Б	В
I	1	2	0
II	2	1	0
III	0	1	1

На складе фирмы имеется 500 ед. ресурса 1, 550 ед. - 2-го, 200 ед. - 3-го ресурса. Прибыль от реализации единицы продукции А составляет 3 руб., Б - 4 руб., В - 1 руб.

Определить:

1) Оптимальный план производства, чтобы прибыль была максимальной,

2) Составить и решить двойственную задачу;

3) Целесообразно ли закупить 250 ед. ресурса 2 по цене С2 = 0,7 руб. за ед.;

4) Целесообразно ли производство четвертого вида продукции Г, если нормы затрат ресурсов на единицу составляют соответственно 3, 1, 2 единицы, а прибыль с единицы продукции равна 5 руб ;

5) Определить изменение максимальной прибыли при изменении ресурсов: 1-го на +70; 2-го на +200; 3-го на - 40 единиц.

Тема 4. Транспортная задача и алгоритм ее оптимального решения

Занятие 3

1. Алгоритм решения транспортной задачи.

2. Методика решения задач в среде MS Excel

Рассмотрим решение транспортной задачи средствами MS Excel на примере задачи, приведенной в теоретическом курсе.

Четыре предприятия для производства продукции получают сырье от трех поставщиков. Потребности в сырье каждого из предприятий (A, B, C, D) равны 20, 110, 40, 110 ед. Сырье имеется в наличии у трех поставщиков, а запасы соответственно равны 60, 120 и 100 ед. На каждое из предприятий сырье может завозиться из любого пункта его получения. Тарифы перевозок являются известными величинами и задаются матрицей

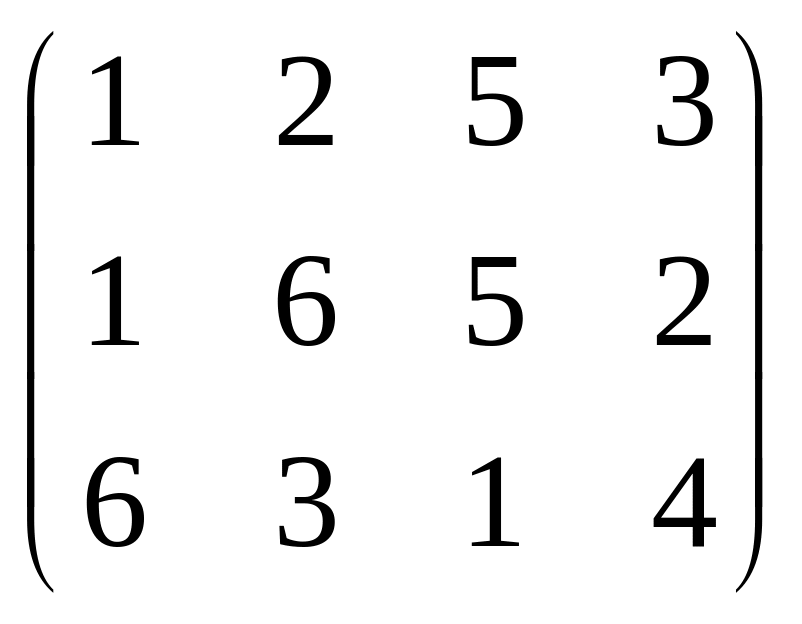
Составить такой план перевозок, при котором общая стоимость перевозок является минимальной.

Обозначим через x_ij количество единиц сырья, перевозимого от i-го поставщика на j-е предприятие. Задача является закрытой, так как сумма запасов сырья у поставщиков составляет 280 единиц, что равно сумме потребностей сырья на предприятиях.

Условия доставки и вывоза необходимого и имеющегося сырья обеспечиваются за счет выполнения следующих равенств:

x₁₁ + x₁₂ + x₁₃+ x₁₄= 60 (1)

x₂₁ + x₂₂ + x₂₃+ x₂₄= 120 (2)

x₃₁ + x₃₂ + x₃₃+ x₃₄= 100 (3)

x₁₁ + x₂₁ + x₃₁ = 20 (4)

x₁₂ + x₂₂ + x₃₂ = 110 (5)

x₁₃ + x₂₃ + x₃₃ = 40 (6)

x₁₄ + x₂₄ + x₃₄ = 110 (7)

При данном плане перевозок x_ij≥0, i=1…3, j=1…4, общая стоимость перевозок составит:

F = x₁₁+2∙x₁₂+5∙x₁₃+3∙x₁₄+x₂₁+6∙x₂₂+5∙x₂₃+2∙x₂₄+6∙x₃₁+3∙x₃₂+x₃₃+4∙x₃₄ → min (8)

Таким образом, математическая постановка задачи состоит в нахождении такого неотрицательного решения системы линейных уравнений (1)–(7), при котором целевая функция (8) принимает минимальное значение.

Перенесем в MS Excel условие задачи в виде таблиц (Рисунок 17):

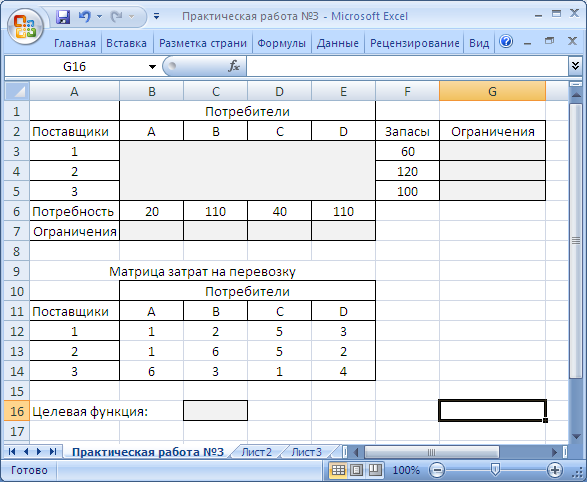
Рисунок 17. Фрагмент листа MS Excel с исходными данными

Ячейки с адресами В3:Е5 резервируются для переменных x_ij – это изменяемые ячейки. В ячейках F3:F5 заносятся запасы сырья у поставщиков, в ячейках B6:E6 заносятся потребности (спрос) сырья на предприятиях. В ячейки с адресами В12:Е14 занесены коэффициенты матрицы затрат на перевозку грузов.

В ячейки G3:G5 заносятся формулы для расчета ограничений (1) – (3). Формула ограничения (1) в ячейке G3 будет иметь вид =СУММ(B3:E3). Соответственно ограничения (2), (3) заносятся в ячейки G4, G5 в виде формул =СУММ(B4:E4), =СУММ(B5:E5).

В ячейках В7:Е7 содержатся формулы ограничений (4)–(7), которые соответственно имеют вид: =СУММ(B3:B5), =СУММ(C3:C5), =СУММ(D3:D5), =СУММ(E3:E5). На Рисунок 18 представлен фрагмент листа в формульном виде.

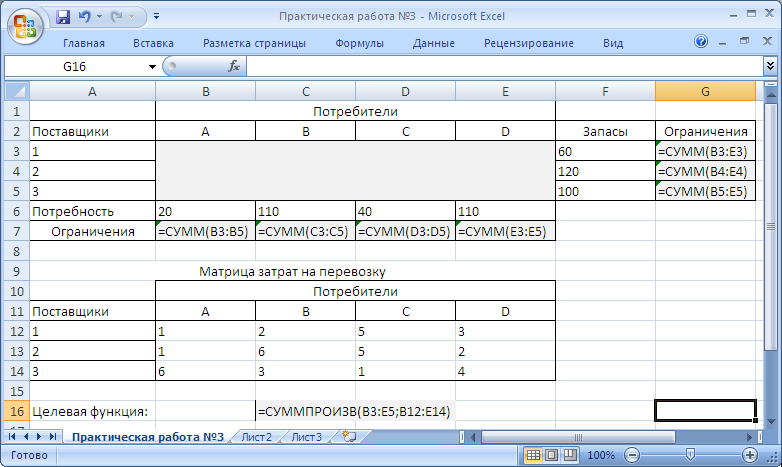
Рисунок 18. Фрагмент листа MS Excel в формульном виде

В ячейки В12:Е14 занесена матрица затрат на перевозки между всеми поставщиками сырья и потребителями.

Формула для расчета Целевой функции (8) занесена в ячейку С16 и имеет вид: =СУММПРОИЗВ(B3:E5;B12:E14). В эту же ячейку будет занесено вычисленное значение целевой функции.

Для решения задачи воспользуемся встроенным в MS Excel инструментом «Поиск решений». Поставим курсор мыши в ячейку С16, в которой будет содержаться вычисленное значение целевой функции, войдем в меню Сервис, выберем в нем Поиск решения (в MS Excel 2007 выберем вкладку Данные – Поиск решения). На экране появится диалоговое окно Поиск решения, заполним его как показано на Рисунок 19.

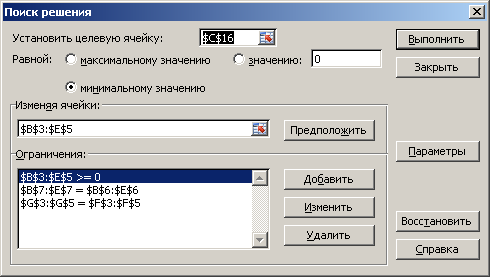
Рисунок 19. Настройка диалога инструмента «Поиск решения»

Нажмем дополнительно кнопку «Параметры», в появившемся диалоговом окне

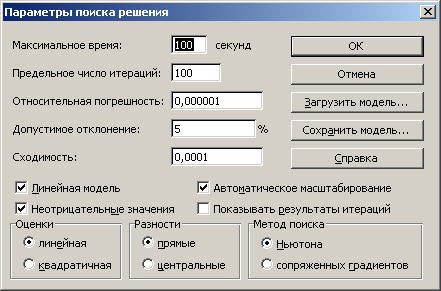
отметим пункты «Линейная модель», «Неотрицательные значения», «Автоматическое масштабирование». Нажмем кнопку «ОК» и «Выполнить».

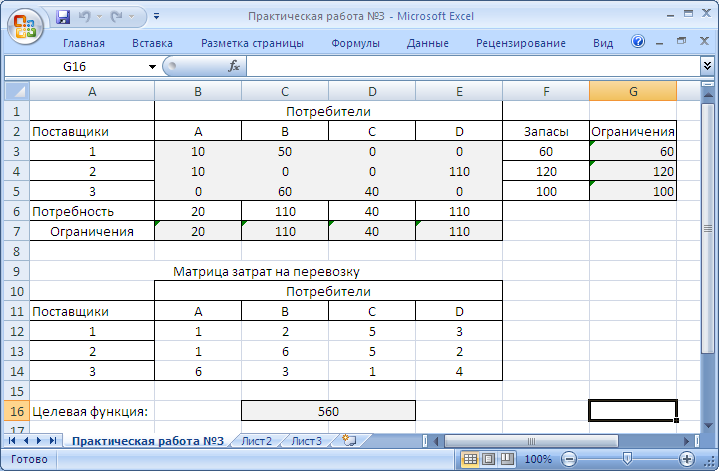
Рисунок 20. Результат выполнения

Видим, что оптимальное решение найдено: при составленном плане перевозок (диапазон ячеек B3:E5) затраты будут минимальны и составят 560 единиц. Все ограничения (G3:G5 и B7:E7) выполнены, все сырье поставлено, все потребности удовлетворены.

Задача 4.1.

На 3-х складах А1, А2, А3 хранятся а1 = 100, а2 = 200, а3 =100 единиц одного и того же груза. Этот груз необходимо доставить потребителям В1, В2, В3, заказы по договорам которых b1 = 190, b2 = 120, b3 = 50 единиц соответственно. Стоимость перевозок Cij единицы груза с i - того склада j - тому потребителю указаны в таблице.

		В1	В2	В3
		b1=190	b2=120	b3=50
А1	а1=100	4	2	5
А2	а2=200	4	5	3
А3	а3=100	1	6	6

Составить оптимальный план перевозки грузов с целью минимизации транспортных расходов.