Тема 3. Симплексный метод оптимизации решений экономических задач

Занятие 2

1. Экономическая сущность симплекс-метода и область его применения в решении экономических задач.

2. Методика отыскания оптимального решения.

3. Двойственные задачи и алгоритм их решения.

4. Методика решения задач средствами MS Excel

Для решения задач симплекс методом с иcпользованием прикладных программных продуктов наиболее оптимальным является применение табличного процессора MS Excel, при помощи которого задача симплекс-метода решается в табличной форме.

Алгоритм составления симплекс таблиц на примере задачи на максимум:

1. Система ограничений записывается в форме уравнений, введя дополнительные переменные x_n+i≥0, i=1,2,…, m.

Уравнение z-c₁x₁-c₂x₂-…-c_nx_n=c₀, полученное переносом всех переменных в левую часть целевой функции, называют оценочным уравнением.

2. Заполняется первая симплексная таблица (см. таблицу 1):

- в первом столбце записываем базисные переменные;

- во втором – свободные члены;

- в третьем и последующих – коэффициенты при переменных x1, x2, …, xn+m;

- в предпоследнем столбце – оценочные отношения;

Таблица1. Заполнение симплекс-таблицы

Базисные переменные	bi	Коэффициенты								Оценочные отношения
		x1	x2	…	xn	xn+1	xn+2	…	xn+m
xn+1	b1	a11	a12	…	a1n	1	0	…	0
xn+2	b2	a21	a22	…	a2n	0	1	…	0
…	…	…	…	…	…	…	…	…	…
xn+m	bm	am1	am2	…	amn	0	0	…	1

Рассмотрим стандартную задачу на распределение ресурсов на примере задачи, разобранной в теоретическом курсе и практической работе №1. Приведем систему ограничений нашей задачи к каноническому виду, введя дополнительные переменные X3, X4, X5, X6:

F=2X1+3X2+0*X3+0*X4+0*X5+0*X6

Построим в MS Excel симплекс таблицу, приведенную на рисунке 9.

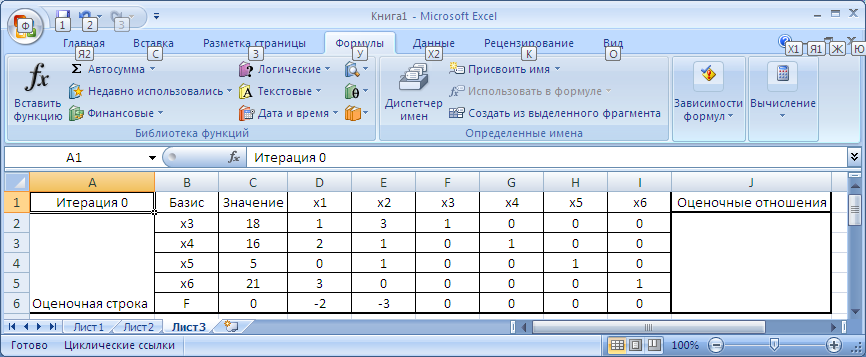
Рисунок 9. Построение первой симплекс таблицы

Данная таблица расположена в диапазоне ячеек А1:J6. В колонку B (B2:B5) запишем перечень наших базисных переменных. Для первого базисного решения такими переменными являются дополнительные переменные X3-X6. В колонку C (C2:C5) запишем правую часть нашей системы уравнений. В колонки D-I (D2:I5) внесем коэффициенты при соответствующих переменных нашей системы уравнений. Последняя строка таблицы (F6:I6) называется оценочной. В нее запишем коэффициенты при соответствующих переменных нашей целевой функции с противоположным знаком.

Если в оценочной строке все числа, начиная с колонки D положительные, то данная итерация дает нам оптимальное решение нашей задачи. Если в оценочной строке имеется хотя бы одно отрицательное число, то решение не оптимальное и имеется возможность отыскать лучшее (не худшее) решение в следующей итерации.

Шаг 1. В оценочной строке выбираем отрицательное число с наибольшим модулем и:

- если в соответствующем столбце имеется хотя бы один положительный коэффициент, то возможен переход к лучшему решению;

- если же все коэффициенты отрицательные, то задача не имеет конечного оптимума.

В нашем случае это колонка E (E2:E6). Выделим ее серым цветом. Это – разрешающая колонка.

Шаг 2. Вычисляем оценочные отношения для каждой строки. Оценочные отношения равны:

- ∞, если b_i ≥ 0, a_ip < 0,

- ∞, если a_ip = 0,

- 0, если b_i = 0, a_ip > 0,

- b_i/a_ip, если b_i ≥ 0, a_ip > 0

Строка, в которой находится минимальное значение оценочного отношения, называется разрешающей строкой. В нашем случае это строка 4. Выделим ее серым цветом, как показано на рисунке 10. Если имеется несколько одинаковых оценочных отношений, то выбираем любое из них.

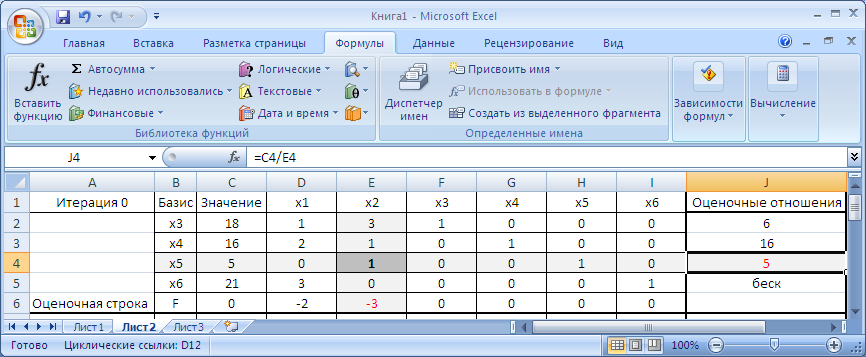
Рисунок 10. Нахождение разрешающей строки, столбца, ячейки

Ячейка на пересечении разрешающей строки и столбца дает нам разрешающий элемент (он обозначается α). Выделим его для наглядности темно-серым цветом.

Шаг 3. Построим вторую симплекс таблицу, аналогичную первой (рис. 11).

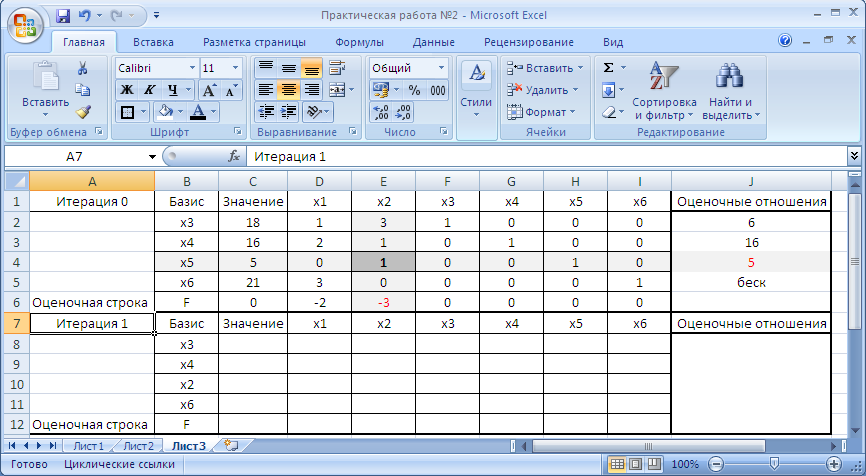
Рисунок 11. Построение второй симплекс таблицы

Заполняем вторую симплекс таблицу:

- определим новый базис – переменную разрешающей строки (в нашем случае переменная X5) заменяем переменной разрешающего столбца (в нашем случае переменная X2), остальные оставляем;

- если α≠1, то все элементы разрешающей строки делим на α, чтобы получить разрешающий элемент, равный 1, и полученную таким образом строку пишем в новой таблице на прежнем месте. В нашем случае разрешающий элемент в ячейке Е4 = 1, таким образом переносим значения ячеек С4:I4 в ячейки С10:I10 (рис.12);

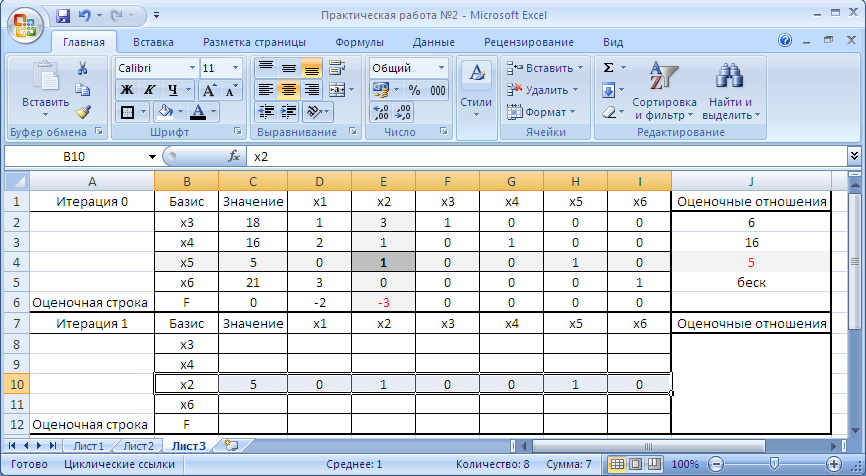
Рисунок 12. Перенос значения разрешающей строки из первой симплекс-таблицы

- нулим разрешающий столбец: к каждой из остальных строк прибавляем вновь полученную строку, умноженную на такое число, чтобы в разрешающем столбце получился 0, полученные строки пишем в новой таблице на тех же местах. В нашей задаче, например значение ячейки С8 будет равно C2+C10*(0-E2)=C2-C10*E2 (рис. 13);

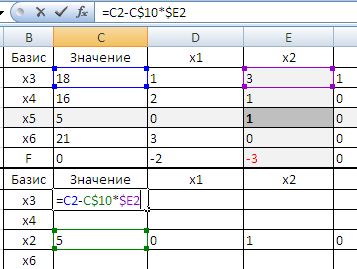
Рисунок 13. Вычисление значения ячеек

- аналогичные значения необходимо скопировать и в остальные ячейки, предварительно корректно зафиксировав необходимые части адреса: =C2-C$10*$E2 (рис. 14).

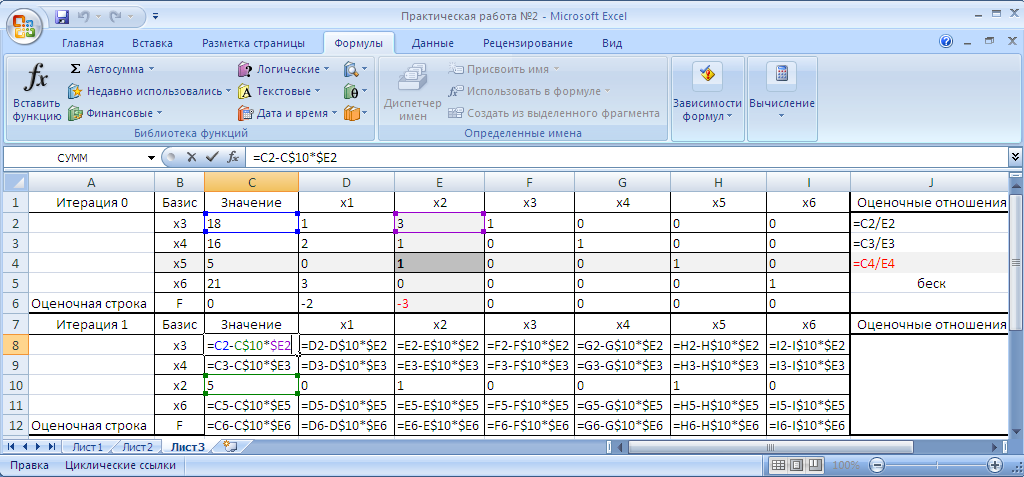
Рисунок 14. Заполнение ячеек второй симплекс таблицы

Шаг 4. Просматриваем оценочную строку:

- если все числа положительны, то решение оптимальное, максимальное значение функции равно свободному члену оценочной строки; а оптимальное решение определяется свободными членами при базисных переменных, все свободные переменные равны 0;

- если в оценочной строке имеется хотя бы один отрицательный элемент, то решение не оптимально, необходимо повторить шаги 1-4.

Для нашей задачи оптимальное решение будет найдено после итерации 3. Финальный вид полученных симплекс-таблиц в формульном виде приведен на рисунке 7, в числовом виде на рисунке 15.

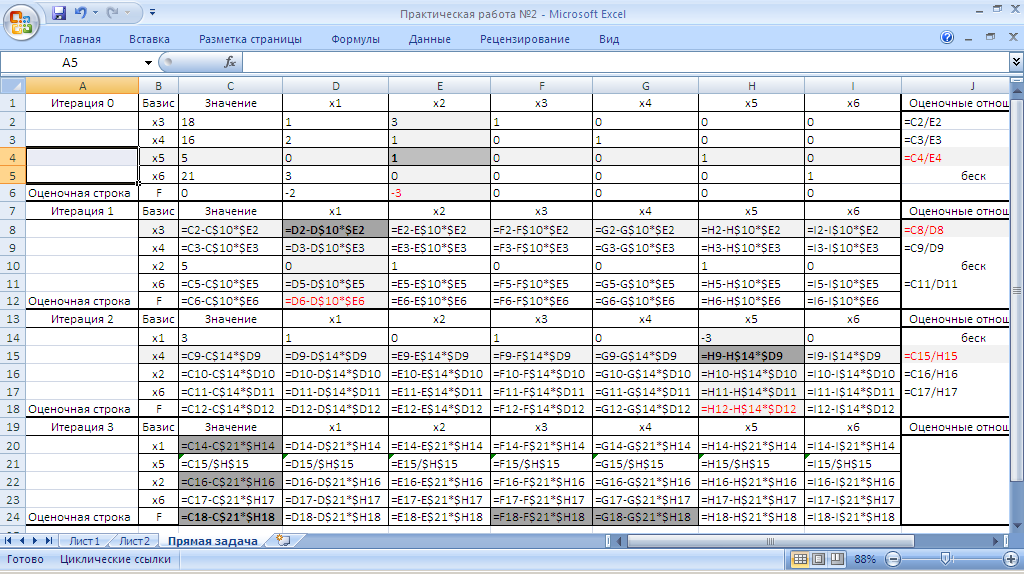
Рисунок 15. Симплекс таблица в формульном виде

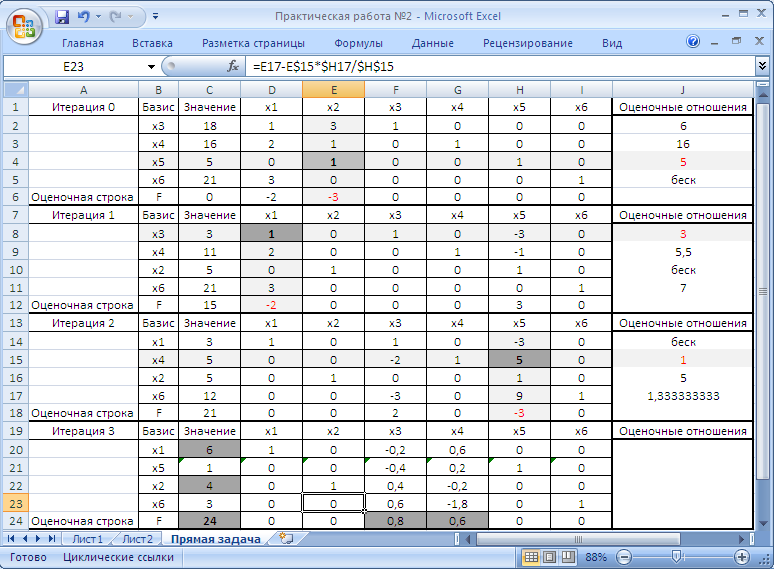
Рисунок 16. Симплекс таблица в числовом виде

Видим, что в оценочной строке все элементы положительные, значит оптимальное решение найдено X_опт=(6; 4; 0; 0; 1; 3). Максимальное значение функции равно свободному члену оценочной строки, находящемуся в ячейке С24, Z_max=24. Значения Х1 и Х2, при которых функция принимает максимальное значение равно значению соответствующих свободных членов в столбце C (X1 – C20, X2 – C22). Остаток ресурса с из задачи равен значению свободного члена в ячейке С21, остаток ресурса d из задачи равен значению свободного члена в ячейке С23. Конечный вид целевой функции на после последней итерации F=24-0,8*X3-0,6*X4 → max.

Задача 3.1.

Для изготовления двух видов продукции Р1 и Р2 используют три вида сырья.

Исходные данные

Вид ресурса	Запас ресурса	Норма расхода сырья на единицу продукции
		Р1	Р2
S1 S2 S3	4770 5610 4820	9 5 7	5 11 8

Прибыль от единицы продукции Р1 составляет 16 у.е., от единицы продукции Р2 - 23 у.е. Составить план производства, при котором получаемая предприятием прибыль была бы максимальной.