3. Практические занятия

Тема 2. Теоретические основы методов линейного программирования в оптимизации экономических решений.

Занятие 1.

1. Общая постановка экономической задачи оптимизации использования ресурсов, составления рациона, использования производственных мощностей, оптимального раскроя материалов.

2.Геометрический метод решения задачи линейного программирования и его экономический смысл.

3.Методика решения задач в среде MS Excel:

Условие задачи:

Для изготовления 2-х видов продукции A и B используют 4 вида ресурсов – a, b, c, d. Прибыль, получаемая от реализации продукции А составляет 2 у.е., продукции B – 3 у.е.

Построить оптимальный план производства продукции A и B, для получения максимальной прибыли.

Вариант 1. Графическое решение в среде Excel:

1. Проанализируем условие задачи, составим математическую модель целевой функции, систему ограничений.

2. Для удобства работы перенесем условие задачи, целевую функцию и систему ограничений в среду MS Excel, как показано на рисунке 1 (диапазон ячеек A1:D19)

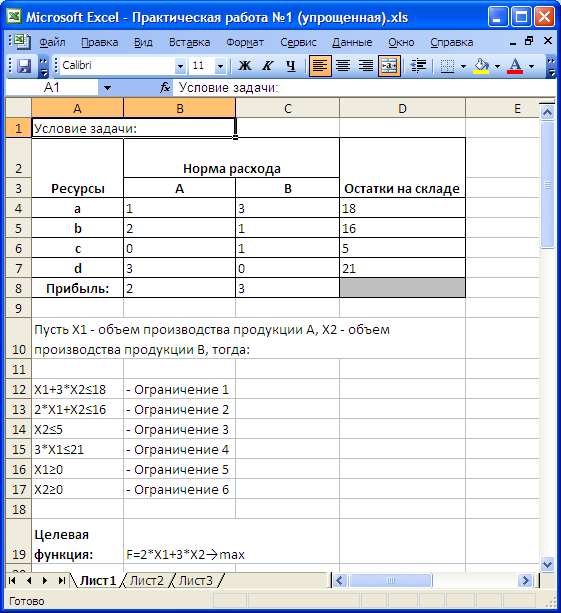
Рисунок 1. Условие задачи. Диапазон ячеек A1:D19

3.1. Приведем ограничения 1-4 к каноническому виду, заменив неравенства на уравнения. Выразим в уравнениях Х2 через Х1 (рисунок 2. Диапазон ячеек С12:Е15)

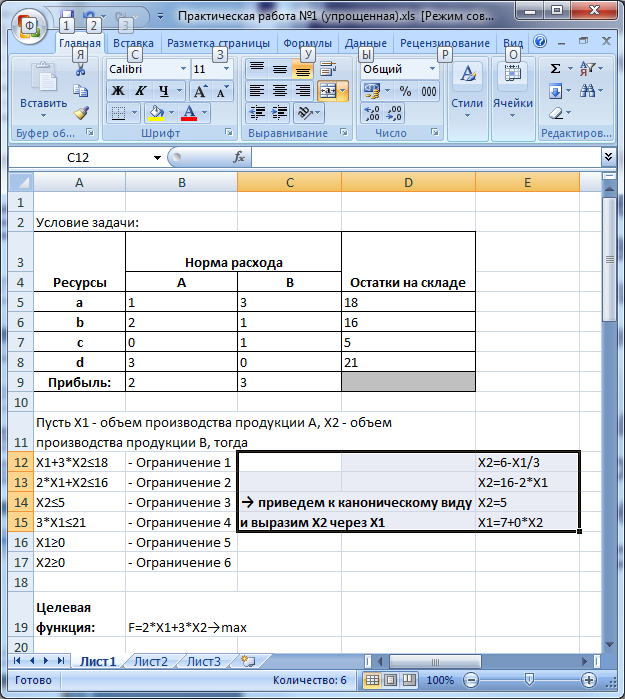
Рисунок 2. Диапазон ячеек С12:Е15

3.2. Получим таблицу значений функции Х2(Х1) для построения графиков функций в декартовой системе координат (рисунок 3. Диапазон ячеек А23:F27). Для этого в столбце А таблицы Excel зададим значения 2-х аргументов Х1 равных 0 и 10. В столбце B введем формулу зависимости Х2(Х1) для первого ограничения: =6-А24/3

Аналогично в столбцах C, D, E зададим формулы зависимости Х2(Х1) для ограничения 2,3,4.

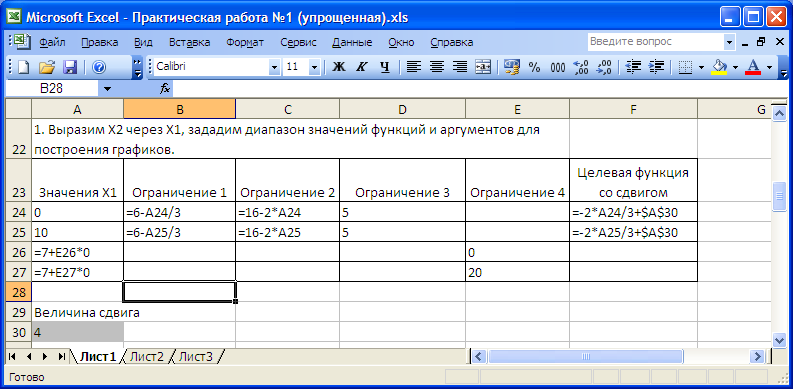
Рисунок 3. Таблица значений функции X2(X1)

Кроме того в столбце F введем формулу зависимости целевой функции, прибавив к ней произвольную константу (в нашем случае в виде значения ячейки A30).

=-2*A24/3+$A$30

Задавая различные возрастающие значения константе можно добиться того, что прямая, описывающая целевую функцию F, смещаясь параллельно себе, будет проходить через одну из вершин полученного многоугольника допустимых решений.

4. Выделяем диапазон значений А23:F27, задаем команду «Вставка/Диаграмма…». В открывшемся окне Мастер диаграмм выбираем Тип: «Точечная»; Вид «Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров». Нажимаем кнопку «Далее».

Задаем параметры диаграммы и нажав кнопку «Готово» получаем рисунок (рисунок 4.).

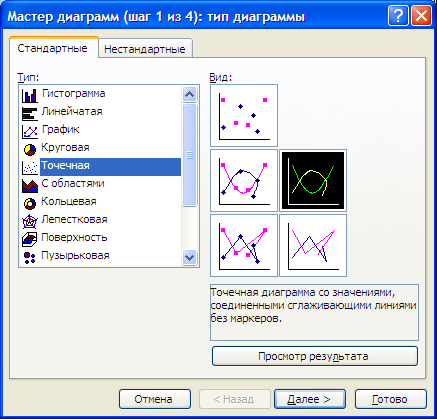
Рисунок 4. Вставка диаграммы

5. При необходимости отформатируем полученную диаграмму:

- выделим ось Х и выберем "Формат оси". Установим минимальное значение 0, максимальное значение 10

- выделим ось Х и выберем «Добавить основные линии сетки»

- при необходимости изменим цвет и толщину линий графиков

Мы получили многоугольник допустимых решений для нашей системы неравенств. Поскольку Excel не умеет автоматически заштриховывать нужную область, то ее границы предстоит определить и при необходимости заштриховать самостоятельно.

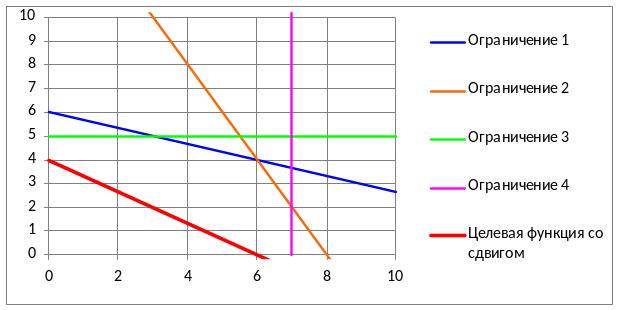
Рисунок 5. Графики системы ограничений

6. Изменяя параметр "Величина сдвига" в ячейке А30 определим, какая из вершин получившегося многоугольника является самой удаленной от начала координат. Эта вершина и будет является оптимальным решением нашей задачи.

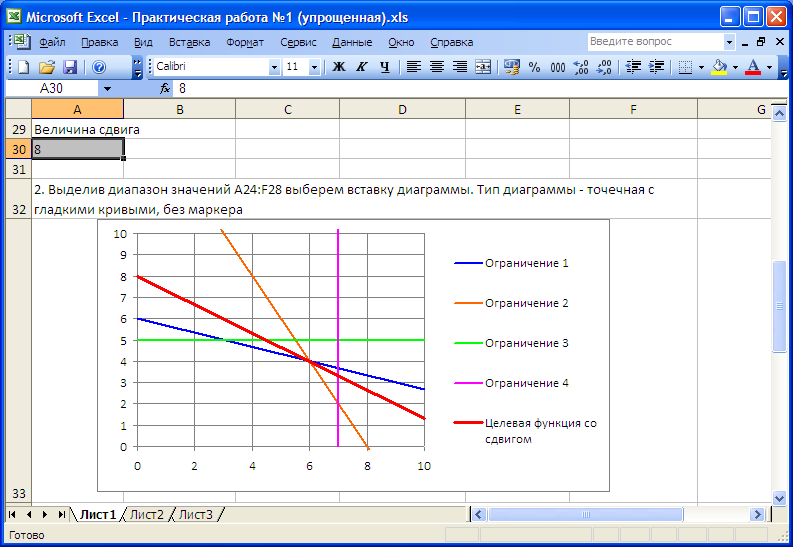
Рисунок 6. Нахождение оптимального решения задачи

Итог:

Из графика следует, что самой удаленной от начала координат вершиной является точка с координатами (6;4). Подставив найденное значение в формулу целевой функции, найдем ее максимальное значение равное 24.

Вариант 2. Решение инструментом "Поиск решения" пакета MS Excel

1. Отведем ячейки А46 и B46 под значения переменных Х1 и Х2.

2. В ячейку А49 введем целевую функцию: =2*A46+3*B46

3. В ячейки А52:А57 введем левые части ограничений: =A46+3*B46; =2*A46+B46; =B46; =3*A46; =A46; =B46

А в ячейки B52:B57 - правые части ограничений (рисунок 7)

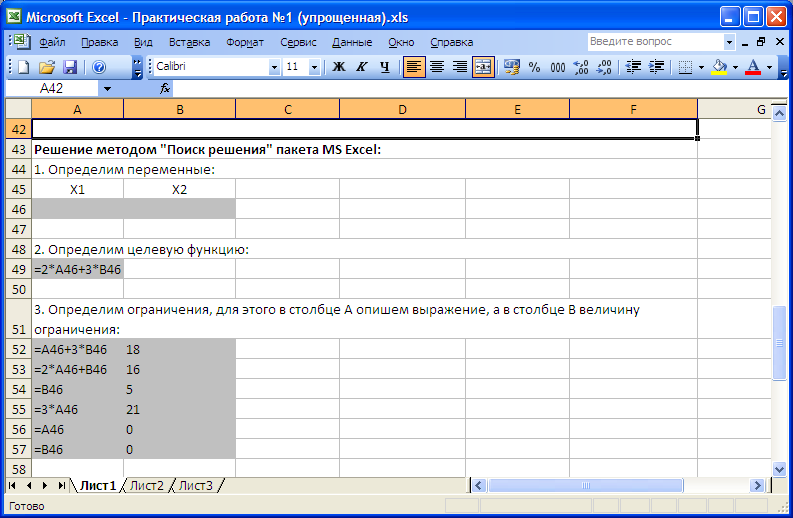
Рисунок 7. Задание условий для поиска решения

4. Выберем команду «Сервис – Поиск решений», и заполним открывшееся диалоговое окно в соответствии с рисунком 8.

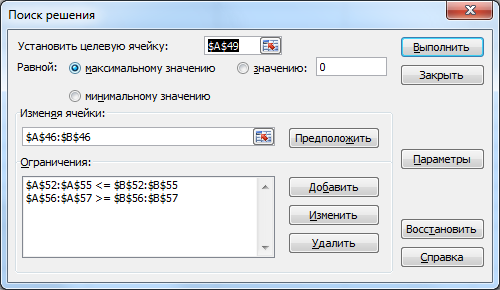
Рисунок 8. Настройка диалога "Поиск решения"

Итог:

По результатам «Поиск решения» видим, что оптимальное решение найдено, и в ячейки А46 и В46 помещены значения 6 и 4 соответственно. Значение целевой функции при этом равно 24.

Задача 2.1.

Для производства двух видов изделий А и В предприятие использует три вида сырья.

Исходные данные

Вид сырья	Нормы расхода сырья на одно изделие, кг		Общее количество сырья, кг
	А	В
1	12	4	300
2	4	4	120
3	3	12	252
Прибыль от реализации одного изделия	30	40

Составить такой план производства продукции, при котором прибыль предприятия от реализации продукции будет максимальной при условии, что изделие В надо выпустить не менее, чем изделие А.