2. Экономические задачи, сводящиеся к транспортным моделям

1. Задача оптимального распределения оборудования

Пусть m-видов оборудования нужно распределить между n-участками. Производительность единицы оборудования i-того вида на j-том участке равна p_ij. Потребность j-того участка в оборудовании составляет b_j, а запас оборудования i-того вида – а_i. Найти распределение оборудования, при котором суммарная производительность, была бы максимальной.

При решении задачи важно, чтобы зависимость между производительностью и количеством оборудования была линейной, тогда задачу можно решить как транспортную. При этом поставщиком будут являть визы оборудования, потребителями – рабочие участки. Предложение – это запас оборудования по видам, спрос – потребность рабочих участков.

Если х_ij – число единиц i-того оборудования, распределенных j-тому участку, то max суммарная производительность оборудования (спрос);

Для перехода к решению транспортной задачи необходимо функцию F заменить на противоположную -F и находить ее минимум.

Вместо тарифов на перевозки записать производительность оборудования p_ij со знаком «-»

Вид оборудования	Запас оборудования	Потребность в оборудовании участок
		1	2	3	4
1	а1	b1	b2	b3	b4
		-p11	-p12	-p13	-p14
2	а2	-p21	-p22	-p23	-p24
3	а3	-p31	-p32	-p33	-p34

2. Задача формирования оптимального штата фирмы

Пусть фирма располагает n-группами различных должностей. По b_j вакантных единиц в каждой группе, j=1, 2 …n. Кандидатуры на должность проходят тестирование по результатам которого их разделяют на m – групп по a_i кандидатов в каждой группе, i = 1, 2 …m. Для каждого кандидата требуются C_ij затраты на обучение для занятия должности. Если С_ij = 0, то кандидат полностью соответствует должности. Требуется занять имеющиеся вакансии с минимум затрат на обучение.

В роли поставщиков выступают кандидаты, в роли потребителей – группы должностей.

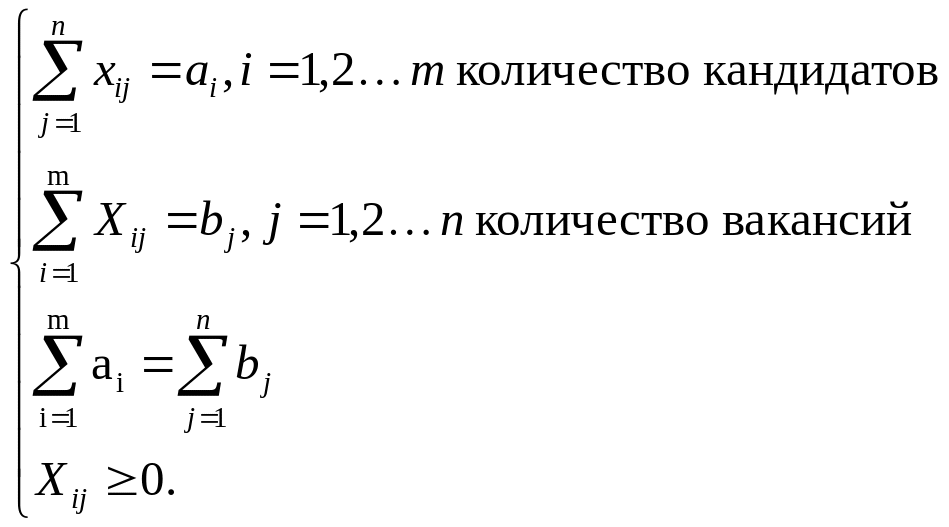
Тема 5. Элементы теории игр в решении экономических задач

Вопросы для изучения:

1. Сущность теории игр и их классификация

2. Методика решения экономических задач с использованием теории игр.

Литература: 1, 7, 18.

1. Сущность теории игр и их классификация.

Часто бывает необходимо принять решение в ситуации, когда две или более сторон при решении вопроса преследуют различные цели. Такие ситуации сопровождаются возможными конфликтами, когда партнеры, имея различные цели, пытаются их решить за счет другой стороны. При этом важно использовать специальные методы, называемые теорией игр, позволяющие принять решение в условиях неопределенности ситуаций.

Математическая модель конфликтной ситуации называется игрой, а стороны – участники называются игроками, исход конфликта определяется выигрышем.

Для разрешения ситуации вводятся правила, или система условий, определяющих:

1. варианты действий игроков;

2. объем информации каждого игрока о поведении партнеров;

3. выигрыш при каждом варианте действий.

Игра называется парной, если в ней участвует два игрока, и множественной, если число игроков больше двух.

Если выигрыш одного игрока равен проигрышу другого игрока, то такая игра называется антагонистической. Рассматривают личные ходы игрока, т.е. сознательные действия, и случайные ходы.

Стратегию игрока определяет совокупность личных ходов в зависимости от сложившейся ситуации.

Игра называется конечной, если у каждого игрока имеется конечное число стратегий, и бесконечной в противном случае.

Для решения игры необходимо для каждого игрока выбрать стратегию, которая удовлетворяет условию оптимальности, т.е. один из игроков должен получить максимальный выигрыш, когда другой игрок придерживается своей стратегии. В то же время игрок должен иметь минимальный проигрыш, если первый придерживается своей стратегии.

Оптимальные стратегии должны быть устойчивыми, т.е. любому из игроков должно быть невозможно отказаться от своей стратегии.

Целью теории игр является определение оптимальной стратегии для каждого игрока.

Теория игр была впервые изложена в 1944 году в виде системы, предлагаемой для решения именно экономической ситуаций.