7. Расчет магнитной цепи синхронной машины при холостом ходе

Цель расчета - определение тока возбуждения I_f и МДС возбуждения

.

Расчет ведется обычно при ЭДС возбуждения E_f =0,5U_ном; U_ном; k_EU_ном; 1,2U_ном, (для генераторов – k_E ≈ 1,08, для двигателей k_E ≈ 1,06; для компенсаторов k_E ≈ 1,13). При E_f=k_EU_ном индукции в стальных участках не должны превосходить допустимых значений.

Порядок расчета:

1). Магнитная цепь синхронной машины разбивается на участки – ярмо статора, зубцовая зона статора, воздушный зазор, сердечники полюсов (для явнополюсных машин) или зубцовая зона ротора (для неявнополюсных), ярмо ротора.

2). По заданной ЭДС E_f определяется магнитный поток взаимной индукции:

.

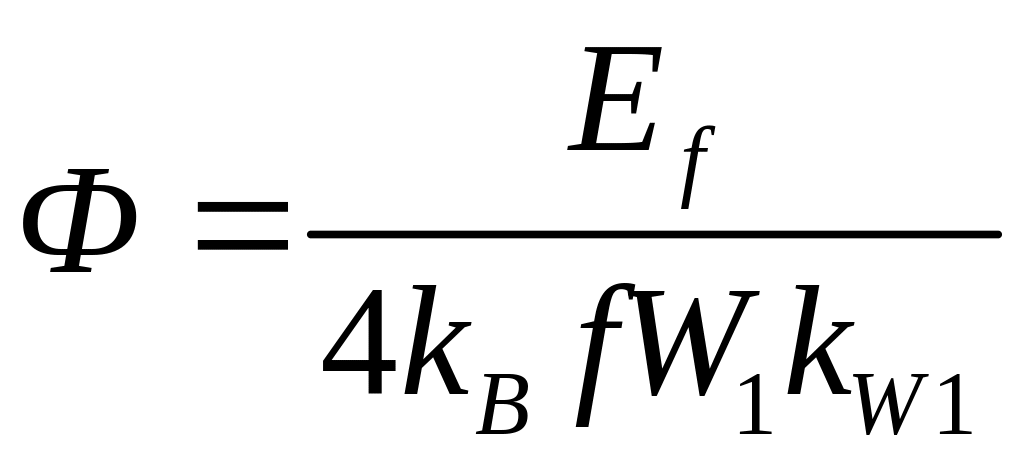Магнитный поток в роторе определяется учетом рассеяния обмотки возбуждения:

Ф_m =Фσ_m,

где σ_m – коэффициент рассеяния полюсов.

3). Определяются значения магнитных индукций на каждом участке магнитной цепи:

.

4). Определяется напряжения магнитного поля H_i на каждом из участков по кривым намагничивания стали В_i =f(H_i).

5). Определяются МДС участков магнитной цепи статора и воздушного зазора:

5.1) в воздушном зазоре

F_ =B_  k_ / ₀

где k_ - коэффициент зазора.

5.2) в зубцовой зоне статора

,

где h_z – высота зубца, H_{z ср} – среднее напряжение поля в зубце

5.3) в ярме статора

F_a1 = k_a1H_a1L_a1

где H_a1 – напряжение магнитного поля в ярме статора; L_a1 – длина средней линии ярма статора

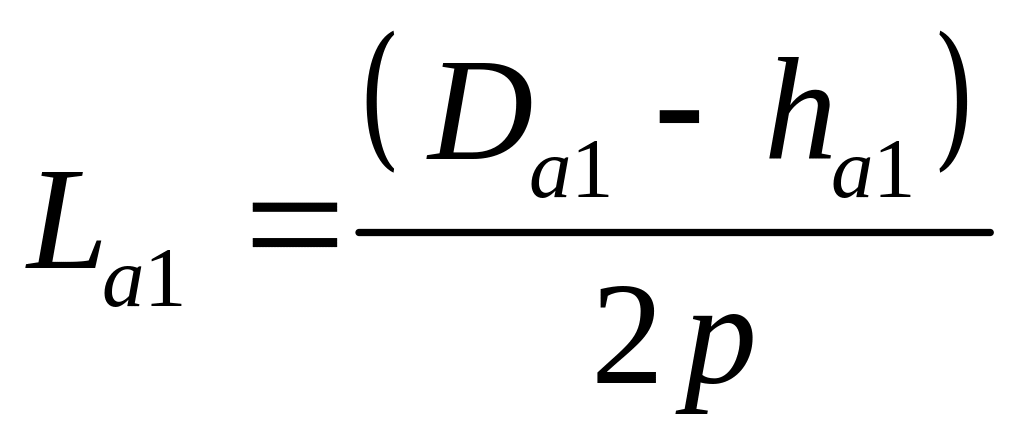
где h_a1 – расчетная высота ярма; D_a1 – диаметр ярма

6). Определяется магнитное напряжение цепи статора и зазора:

F₁ = F_ + F_z1 + F_a1

7). Определяется коэффициент насыщения (в явнополюсной машине), 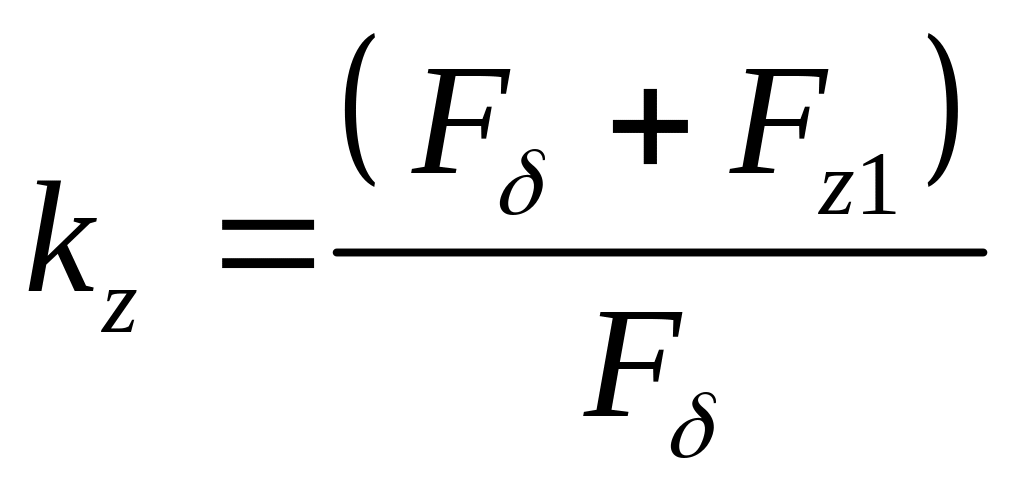( в неявнополюсной машине). Если он значительно отличается от ранее принятых значений, то расчет повторяют сначала с новыми значениями параметров.

8). Определяют коэффициент рассеяния полюсов:

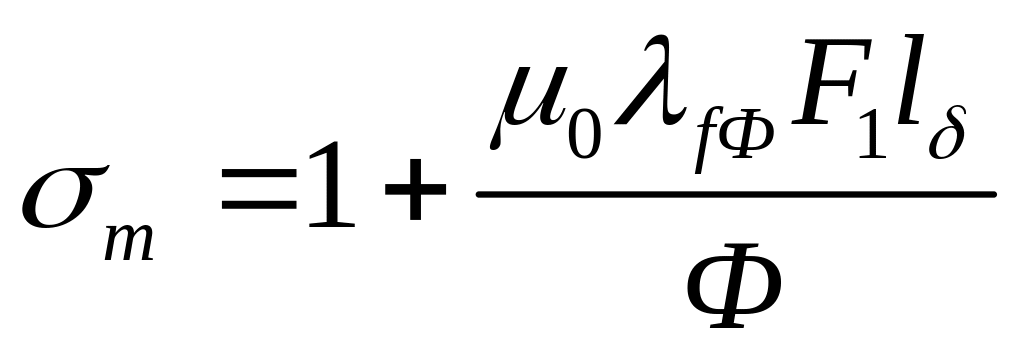
где λ_fФ – коэффициент проводимости для потока рассеяния полюсов

9). Определяются МДС участков магнитной цепи ротора:

9.1) в ярме ротора

F_a2 = L_a2 H_a2

9.2) в зубцовой зоне ротора (для неявнополюсных)

F_z2 = h_z2 H_z2,

где h_z2 – высота зубца, H_z2 – напряжение поля в зубце.

9.3) в полюсах (для явнополюсных):

F_m = H_m h_m

9.4) в стыке между полюсами и ярмом (для явнополюсных):

10). Определяется магнитное напряжение цепи ротора:

- для явнополюсных

F₂ = F_m + F_m + F_a2

- для неявнополюсных

Магнитное напряжение ротора .

11) Результирующая МДС возбуждения

;

где k_H – коэффициент насыщения магнитной цепи.

По результатам расчета магнитной цепи строятся характеристика холостого хода и характеристики намагничивания.

К характеристикам намагничивания относятся основная характеристика намагничивания Ф = f ( F_f ), переходная характеристика намагничивания Ф = f ( F₁ ), характеристика намагничивания сердечника ротора Ф_m = f ( F₂ ) и характеристика намагничивания для потока рассеяния Ф_{f } = f ( F₁ ), где Ф_{f } = Ф_m – Ф.

8. Магнитное поле обмотки якоря синхронной машины

При работе под нагрузкой магнитное поле в зазоре синхронной машины создается МДС обмотки возбуждения и МДС обмотки якоря. Основную роль в процессе преобразования энергии играет основная гармоническая индукции поля в зазоре, которую называют полем взаимной индукции. Точный расчет этого поля с учетом насыщения магнитной цепи и конструктивного исполнения ротора является весьма сложной задачей.

Поэтому при допущении о бесконечно большой проницаемости стальных участков поле взаимной индукции может быть представлено как сумма основных гармонических полей созданных МДС обмотки возбуждения и основной гармонической МДС обмотки якоря.

Магнитное поле обмотки якоря можно представить в виде суммы двух полей, созданных продольной составляющей МДС обмотки F_d, ось которой совпадает с осью полюса d, и поперечной составляющей F_q, ось которой совпадает с осью межполюсного пространства:

Продольная и поперечная составляющие тока якоря:

где ψ – угол между ЭДС E_f и током якоря I.

В зависимости от режима нагрузки продольная система токов I_1d может быть намагничивающей (рис. 24.52, в) или размагничивающей.

Поле от продольной составляющей МДС якоря характеризуется коэффициентом формы поля по продольной оси, который равен отношению основной гармоники индукции от продольной МДС к амплитуде индукции от этой МДС:

.

Поле от поперечной составляющей МДС якоря характеризуется коэффициентом формы поля по поперечной оси, который равен отношению основной гармоники индукции от поперечной МДС якоря к амплитуде индукции от этой МДС:

.

Для неявнополюсной машины:

.

Магнитодвижущая сила обмотки якоря F_a, ее продольная и поперечная составляющие F_d, F_q отличаются по форме от МДС обмотки возбуждения F_f. Магнитодвижущая сила якоря распределена по поверхности якоря синусоидально; распределение МДС возбуждения значительно отличается от синусоидального. Это затрудняет сложение МДС якоря и МДС возбуждения при расчете режимов работы машины. Поэтому для упрощения расчетов синусоидальные МДС якоря заменяются эквивалентными МДС обмотки возбуждения, определенными из условия сохранения основных гармонических индукции в зазоре и ЭДС обмотки якоря.

МДС обмотки возбуждения, эквивалентная МДС обмотки якоря по продольной оси:

где — коэффициент реакции по продольной оси.

МДС обмотки возбуждения, эквивалентная МДС обмотки якоря по поперечной оси:

где — коэффициент реакции по поперечной оси.

Обычно , .

Для неявнополюсной машины МДС обмотки якоря, эквивалентная МДС обмотки возбуждения:

где — коэффициент формы поля возбуждения.