42. Релейно-контакторное управление в функции скорости переходными процессами эд, питающихся от сети. Устройства контроля скорости. Пример схемы и пусковой диаграммы.

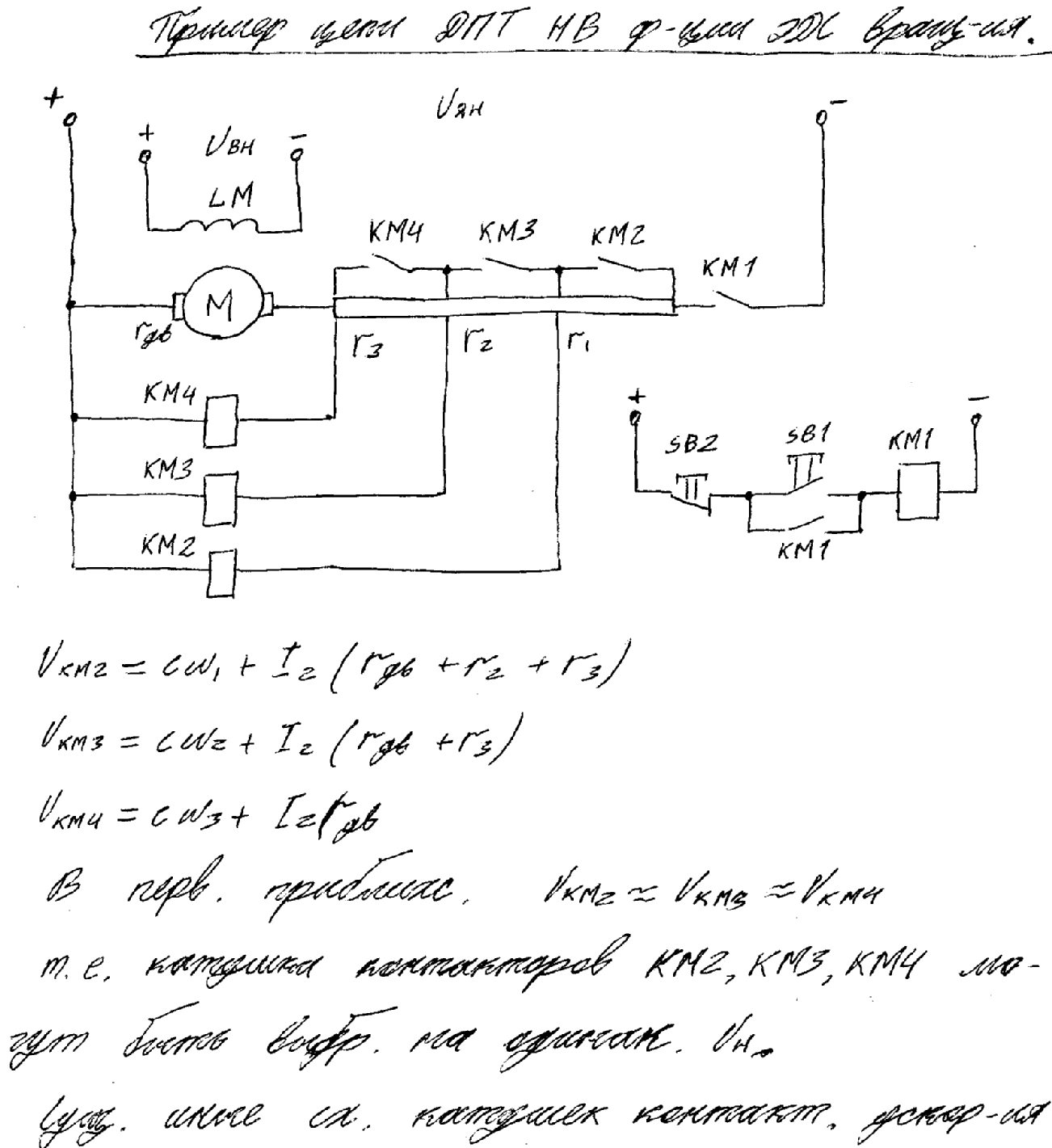
43. Релейно-контакторное управление в функции времени переходными процессами эд, питающихся от сети. Устройства контроля времени. Пример схемы и пусковой диаграммы.

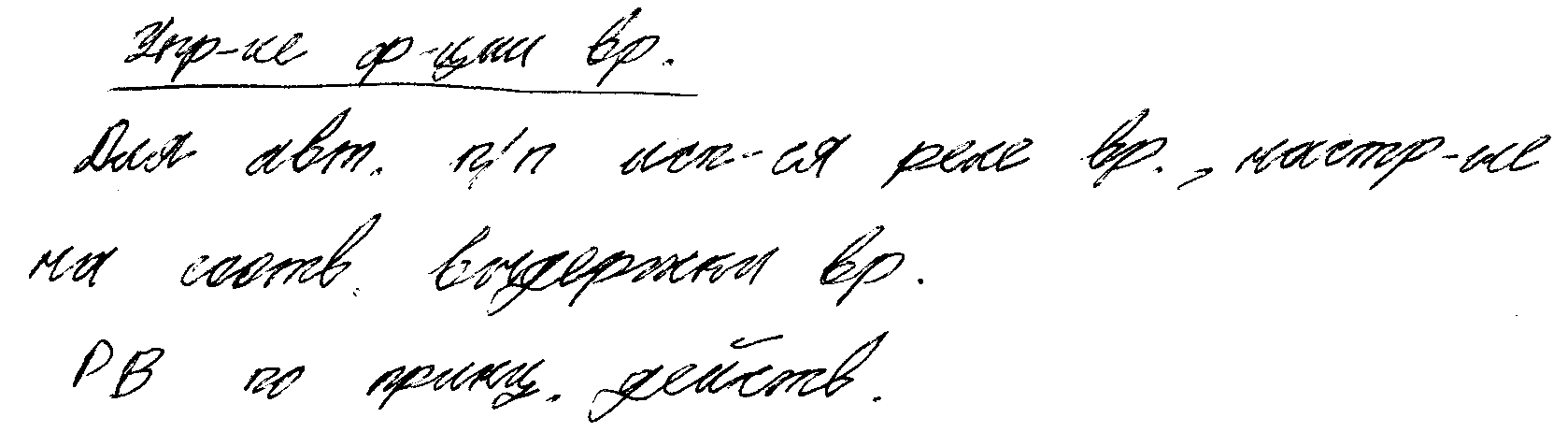
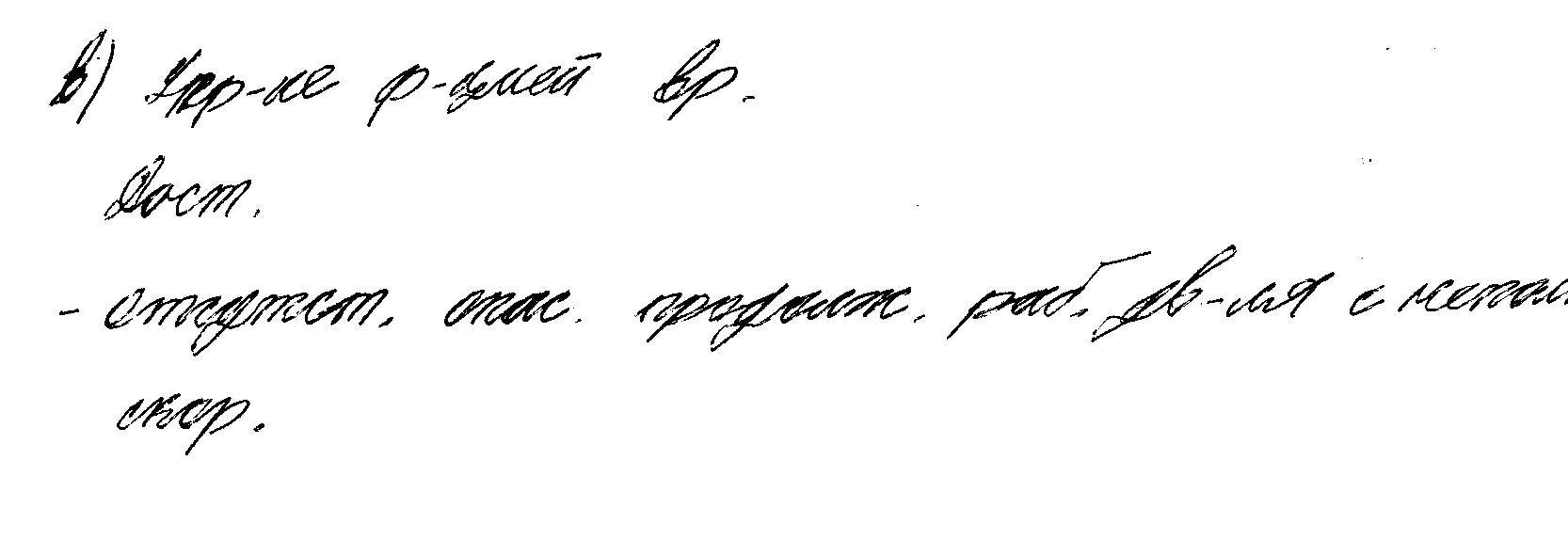
45. Нагрев и охлаждение эд. Одноступенчатая тепловая теория. Коэффициент изменения теплоотдачи.

В тепловом отношении ЭМ – сложный объект: она неоднородна по материалу, имеет рассредоточенные внутр. источники тепла, интенсивность кот. зависит от режима, теплоотдача зависит от скорости и т.п. Именно эта сложность побуждает на практ. для относительно грубых оценок предельно простой моделью, построенной в предположении, что машина – однородн. тело с пост. теплоемк. С, Дж/С, с одинаковой темп. во всех точках θ, с коэффициентом теплоотдачи А, Дж/сС.  - разность темп. машины θ и окр. среды θ_ос , т.е.  = θ - θ_ос, С.

Допущения одноступ. тепл. теории:

1) ЭД – однород. тело с бесконечн. теплопроводностью, поэтому во всех его точках температура одинакова.

2) Теплоотдача в окр. среду пропорц. разности температур дв. и окр. среды.

3) Теплоемк. и теплоотдача дв. в окр. среду не завис. от ее темп.

4) Темп. окр. среды и дв. пост.

Тогда ур-ие тепл. баланса для некот. интервала вр. dt будет

Разделив обе части на А dt, получим:

или

где T_т = C/A – тепловая постоянная времени;

_кон = Р/А – конечн. (устан-шееся) знач-ие превыш-ия темп.

При одном накопителе энергии, в данном случае тепловой, переменная, характеризующая ее запас, изменяется по экспоненте:

Пост-ая вр. Т_т - не постоянная: в начальн. части нагрева, когда греются лишь активные части (медь обмоток) и тепло не успевает распростр-ся по всему телу машины, процесс идет быстрее, т.е. Т_т < Т_т – пунктир на рис.

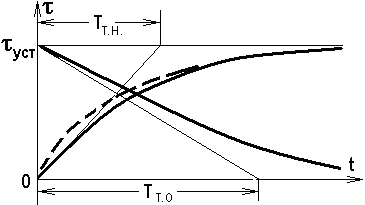
Рис. Характеристики нагревания/охлаждения ЭМ

В установившемся режиме (d /dt =0) имеем ;

Для самовентилируемых машин теплоотдача зависит от скорости, уменьшаясь с ее уменьшением, т.е. Т_=0>T_т , причем разница может быть существенной – в 2 и более раза.

Коэф. ухудш-ия теплоотдачи при неподвиж. роторе β₀=A₀/A_Н

A₀ – теплоотдача неподвиж. ЭД.

A_Н – теплоотдача при номин. скорости ЭД.

- Закр. дв. с независ. вентил. β₀=1

- Закр. дв. с естеств. вентил. β₀=0,95-0,98

- Закр. дв. с самовентил. β₀=0,45-0,55

- Защищен. с самовентил. β₀=0,25-0,35

ω<ω_Н: β=A/A_Н<1; ω>ω_Н: β=A/A_Н>1

β – коэф. измен-ия теплоотдачи, то β₀ – частн. случ.

46. Изменение составляющих потерь в регулируемом асинхронном ЭП: а) при М_с=const, б) при М_с=М_н(/_н).

Принимая равн. объемы актив. стали стат. и рот.

Реостатное регулирование скорости:

Частотное регулирование скорости по закону U/f=const:

Переменные потери:

*

а) M_C=M_Н=const

б) M_C=M_Н(ω/ω_Н)²

**

Макс. потерь опр-ся диф-нием ** по ω, то

ω_max=2/3ω₀ – скорость, при кот. макс. потери

***

Потери в статоре:

Выраж-ия ** и *** справедл. и для реостат. рег-ия ДПТНВ при вентил. типе нагр.

47. Потери энергии в переходных процессах вхолостую эп, у которых задающее воздействие меняется скачком.

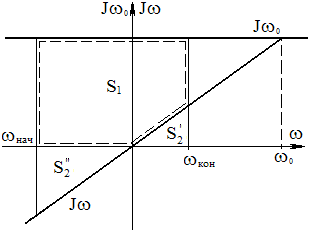
S₁ – энергия, потребл-ая из сети цепью статора (ротора)

S₂ – изменение запаса кин. энергии (полезн. раб.)

Частные случаи:

1) Пуск вхолостую

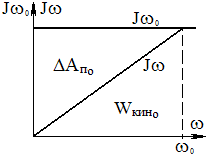
ω_НАЧ=0 S_НАЧ=1; ω_КОН=ω_О S_КОН=0;

Полезн. раб. – создание запаса кинетич. энергии.

Потери

2) Реверс вхолостую

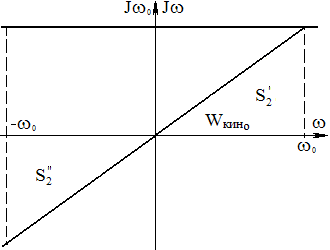
ω_НАЧ=-ω_О S_НАЧ=2; ω_КОН=ω_О S_КОН=0;

Вся потребл. из сети энергия выдел-ся в виде потерь в сил. цепи.

3) Торможение противовключением вхолостую

ω_НАЧ=-ω_О S_НАЧ=2; ω_КОН=0 S_КОН=1;

4) Динамическое торможение вхолостую

ω_НАЧ=-ω_О S_НАЧ=1; ω_КОН=0 S_КОН=0;

Вывод: Потери энергии в якорн. (роторн.) цепи при п/п вхолост., обусл-ых скачкообр. измен-ием упр. возд-ия, не завис. от вида мех. хар-ки дв-ля, а опр-ся только скачком упр-щего возд-ия