12. Координатные преобразования уравнений механической характеристики обобщенной машины.

Рассмотрим преобразования при переходе от физических переменных в системах координат α,β (статора) и d,q (ротора) к расчетным переменным в системе координат и,v, вращающейся относительно непод­вижного статора с произвольной скоростью ω_к. Каждую реальную обмо­точную переменную (напряжение, ток, потокосцепление) представим векто­ром, направленным вдоль соответствующей данной обмотке оси координат, модуль которого меняется во времени в соответствии с изменениями изо­бражаемой переменной.

Взаимное положение на рассматриваемый момент времени систем ортогональных координат α,β (статора), d,q (ротора) и произвольной и,v, a также результирующих векторов обмоточных переменных статора x₁, рото­ра x₂ и их проекций на соответствующие оси показано на рис. Приняв заданными действительные переменные в осях α,β и d,q, можно найти соответствующие им новые переменные в осях и,v в виде суммы проек­ций действительных переменных на новые оси.

Для большей наглядности графические построения выполнены от­дельно для статора (рис.а) и ротора (рис.б) Просуммировав проек­ции векторов x_1α и х_1β на оси и и v (рис.а), получаем формулы прямо­го преобразования переменных статора

*

Оси и,v (рис.б) смещены относительно роторных осей d,q на угол φ_К-φ_ЭЛ и совпадают с осями и,v (рис.а). Следовательно, формулы прямого преобразования роторных переменных имеют вид

**

Из * и ** можно получить формулы обратного преобразо­вания, т. е. перехода от преобразованных переменных в осях и,v к реаль­ным переменным обобщенной машины:

***

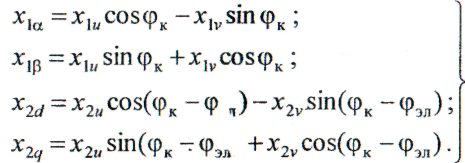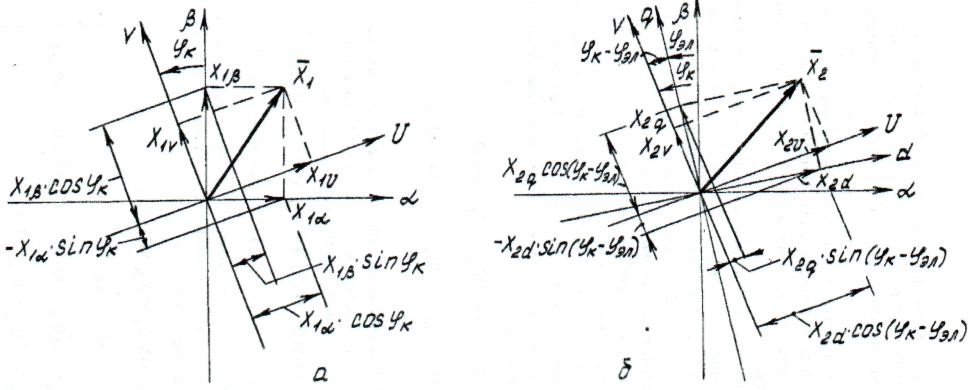
Рис. Переменные обобщенной машины в различных системах координат

Формулы прямого *, ** и обратного *** преобразования координат находят практическое применение при разработке управляющих вычислительных устройств в регулируемых электроприводах переменного тока и при выполнении теоретических исследований этих приводов.

13. Фазные преобразования переменных.

Математическое описание динамической механической характеристики получено для двухфазной модели машины. Обмотка статора большинства двигателей переменного тока чаще всего выполняется трехфазной, поэтому имеется необходимость преобразования переменных трехфазной машины к переменным обобщенной машины и наоборот. Основой для преобразова­ния служит то обстоятельство, что один и тот же результирующий вектор МДС может быть создан как двухфазной, так и многофазной (в частном случае трехфазной) обмоткой.

Пусть задана несимметричная система реальных переменных x_lа, x_1b, х_1с статора трехфазной машины. На основании построения в пред­положении, что преобразованные переменные пропорциональны сумме проекций переменных x_lа, x_1b, х_1с на оси α,β, имеем

*

где к_с - коэффициент пропорциональности, получаемый из условия инва­риантности мощности.

На практике система переменных трехфазной машины обычно явля­ется симметричной, т. е. подчиняющейся условию

**

С учетом ** уравнения * принимают вид

***

Переменные х_2d, х_2q роторной цепи также определяются по * и ** при соответствующей замене индексов.

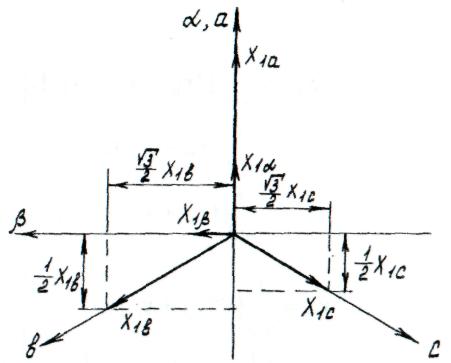
Рис. Схема преобразования переменных трехфазной машины к переменным двухфазной модели

Токи нулевой последовательности не влияют на момент двигателя, поэтому влияние переменных нулевой последовательности на динамику электромеханических систем чаще всего не учитывается.