Гидравлика

ПРИДНЕСТРОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИМ. Т. Г. ШЕВЧЕНКО

Аграрно-технологический факультет

Кафедра эксплуатации и ремонта

машинно – тракторного парка

Гидравлика

Методические указания к выполнению лабораторных работ по курсу по дисциплине "Гидравлика" специальности 110301 «Механизация сельского хозяйства», 110302 «Электрификация и автоматизация», 110303 «Механизация переработки сельскохозяйственной продукции»

Тирасполь 2012

УДК 631.3(07): 631.173.2(07)

ББК 40.72р3 + 74.5

К 49

Составители:

А.Н. Котомчин, ст. преп. кафедры эксплуатации и ремонта машинно-тракторного парка ПГУ им. Т.Г. Шевченко

Г.В. Клинк к.т.н., доц. кафедры эксплуатации и ремонта машинно-тракторного парка ПГУ им. Т.Г. Шевченко

Рецензенты:

Т.В. Боунегру ст. преподаватель кафедры «Автоматизированные технологии и промышленные комплексы» ПГУ им. Т.Г. Шевченко

Н.И. Корнейчук к.т.н., доц. кафедры эксплуатации и ремонта машинно-тракторного парка ПГУ им. Т.Г. Шевченко

Методические указания предназначены для студентов очной и заочной форм обучения специальности 110301 «Механизация сельского хозяйства», 110302 «Электрификация и автоматизация», 110303 «Механизация переработки сельскохозяйственной продукции», выполняющих лабораторные работы по дисциплине «Гидравлика», а также могут быть использованы при выполнении курсовых работ и проектов по специальным дисциплинам и дипломном проектировании.

УДК 631.3(07): 631.173.2(07)

ББК 40.72р3 + 74.5

К 49

Утверждено Научно-методическим советом ПГУ им. Т.Г. Шевченко

© Составитель:

ПГУ им.Т.Г.Шевченко

А.Н. Котомчин, Г.В. Клинк, 2012.

Содержание

Введение........................................................................................4

Лабораторная работа №1 ИЗУЧЕНИЕ ФИЗИЧЕСКИХ СВОЙСТВ ЖИДКОСТИ.......................................................................7

Лабораторная работа №2 ИЗМЕРЕНИЕ ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ И ЭКСПЕРИМЕНТАЛЬНОЕ ПОДТВЕРЖДЕНИЕ ЗАКОНА ПАСКАЛЯ.............................................................................................13

Лабораторная работа №3 ОПРЕДЕЛЕНИЕ ОПЫТНЫМ ПУТЕМ СЛАГАЕМЫХ УРАВНЕНИЯ Д. БЕРНУЛЛИ..................21

Лабораторная работа №4 ЭКСПЕРИМЕНТАЛЬНАЯ ИЛЛЮСТРАЦИЯ ЛАМИНАРНОГО И ТУРБУЛЕНТНОГО РЕЖИМОВ ДВИЖЕНИЯ ЖИДКОСТИ, ОПРЕДЕЛЕНИЕ ЗАКОНОВ СОПРОТИВЛЕНИЯ И КРИТИЧЕСКОГО ЧИСЛА РЕЙНОЛЬДСА...................................30

Лабораторная работа №5 ИЗУЧЕНИЕ ГИДРАВЛИЧЕСКИХ ПОТЕРЬ ПО ДЛИНЕ ТРУБОПРОВОДА И В МЕСТНЫХ СОПРОТИВЛЕНИЯХ........................................................................39

Лабораторная работа № 6 ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ ГИДРАВЛИЧЕСКОГО УДАРА В ТРУБОПРОВОДЕ......................51

ПРИЛОЖЕНИЯ..........................................................................53

ЛИТЕРАТУРА.............................................................................57

Введение

Гидравлика является наукой, где лабораторные эксперименты, а также наблюдения за различными гидравлическими явлениями играют исключительно большую роль. Без широко поставленного лабораторного эксперимента, гидравлика не смогла бы достигнуть уровня своего современного развития. Это объясняется сложностью многих гидравлических явлений, которые приходиться рассматривать и изучать при решении ряда важных инженерных проблем, и необходимостью соответственной корректировки результатов, получаемых с применением различных упрощающих допущений.

Отдельные вопросы гидродинамики в настоящее время еще не могут быть решены теоретическим путем, поэтому приходиться прибегать к нахождению простых эмпирических и полуэмпирических соотношений, необходимых для использования в инженерной практике. Все эти соотношения и формулы могут быть получены в результате постановки соответствующих лабораторных исследований. Следовательно, роль гидравлического эксперимента в решении многих проблем инженерной практики весьма значительна.

В соответствие с вышеизложенным, проведение лабораторных работ по курсу «Гидравлика» ставит перед студентами следующие задачи:

- овладеть методикой постановки и проведения лабораторного гидравлического эксперимента;

- научиться анализировать полученные экспериментальные данные;

- проверить соответствие, полученной опытным путем величины, величинам, вычисленным по аналитическим зависимостям;

- составить характеристику наблюдаемого при эксперименте

гидравлического явления;

- сделать выводы, соответствующие экспериментальным данным;

- получить навыки оформления отчетной документации по проведенным исследованиям.

К занятиям в лаборатории гидравлики допускаются студенты, получившие инструкцию по технике безопасности у преподавателя с соответствующим оформлением студента в журнале.

Студентам запрещается подходить к насосным установкам,

самостоятельно включать электродвигатели, открывать и закрывать задвижки и вентили трубопроводов, включать измерительные приборы. Эти работы должны выполняться либо лаборантом, либо студентами под наблюдением лаборанта или преподавателя.

Оборудование лаборатории относится к разряду особо опасных в отношении поражения электрическим током, поэтому студенты обязаны строго соблюдать правила защиты, уметь оказать помощь пострадавшим от электротока. Перед началом работ преподаватель должен ознакомить студентов с лабораторным оборудованием и правилами пользования им. Прежде чем приступить к работе, необходимо проверить исправность ограждения движущихся частей установок, наличие и крепление заземления, убрать с установок посторонние предметы.

При работе в лаборатории студенту следует выполнять только ту работу, которую поручает ему преподаватель. Запрещается бесцельно ходить по лаборатории, подходить к группе, которая выполняет другую работу, отвлекать разговорами своих товарищей.

При возникновении каких-либо затруднений, немедленно прекратить работу и обратиться за помощью к преподавателю или лаборанту.

Категорически запрещается работать в лаборатории одному.

Запрещается находиться в лаборатории в пальто, вешать одежду на оборудование, снимать запрещающие и предупреждающие плакаты, оставлять установку до конца проведения эксперимента без присмотра.

Закончив выполнение лабораторной работы, необходимо привести в порядок свое рабочее место, поставить в известность об этом преподавателя или лаборанта.

Лабораторная работа № 1 изучение физических свойств жидкости

Цель работы:

Закрепление знаний по разделу "Молекулярная структура и особенно­сти жидкого состояния", получение навыков опытного определения плот­ности, коэффициентов теплового расширения, вязкости и поверхностного натяжения жидкостей.

Теоретическая часть:

Феноменологические свойства жидкости, как сплошной среды, могут существенно изменяться при изменении ее термодинамических парамет­ров. Плотность жидкости ρ возрастает при повышении давления и, как правило, уменьшается при повышении температуры. Последнее свойство характеризуется коэффициентом теплового расширения β_Т, определяющим относительное изменение объема W при изменении температуры Т:

(1.1)

Среднее значение этого коэффициента при увеличении температуры

на ∆Т:

(1.2)

где ∆W ― приращение объема.

Вязкость жидкости с повышением давления несколько увеличивается, с повышением температуры ― значительно уменьшается. В частности, для воды справедлива эмпирическая формула Ж. Пуазейля:

ν = 0,179 · 10-2/ (1000 + 34Т +0,22Т2)

(1.3)

где ν - кинематический коэффициент вязкости, м²/с;

Т - температура, °С.

Поверхностное натяжение жидкости определяется видом газа над ее свободной поверхностью, примесями и температурой. Коэффициент по­верхностного натяжения численно равен силе на единице длины пери­метра свободной поверхности жидкости.

Описание опытной установки:

Экспериментальное устройство состоит из ряда приборов, разме­щенных в общем корпусе (рис.1).

Термометр 1 показывает температуру всех жидкостей, залитых в приборы устройства, а также служит для изучения теплового расши­рения находящейся в нем жидкости (этилового спирта). Термометр имеет стеклянный баллон с капилляром, заполненный термометрической жидкость, и шкалу. Принцип действия прибора основан на тепловом расширении жидкостей. Изменение температуры окружающей среды, а значит, и жидкости вызывает соответствующее изменение ее объема и, следовательно, ее уровня в капилляре. Уровень указывает на шкале значение температуры.

Ареометр 2 предназначен для измерения плотности (определяемой концентрацией) водного раствора спирта поплавковым методом.

Прибор представляет собой пустотелый цилиндр со стержнем в верхней части. Глубина погружения ареометра является функцией плотности. Шкала на стержне проградуирована в процентах концентрации спирта.

Вискозиметр Стокса 3 позволяет определить вязкость жидкости по скорости падения в ней шарика. Прибор содержит цилиндрическую полость с центрирующими каналами на концах, заполненную водно-глицериновым раствором, и шарик. Центрирующие каналы обеспечивают падение шарика по оси полости.

При равномерном движении шарика выполняется условие равенства нулю суммы действующих на него сил:

(1.4)

Здесь P – сила тяжести,

Q– архимедова сила,

F– сила сопротивления движению.

Сила тяжести находится по уравнению:

(1.5)

где ρ_ш– плотность материала шарика;

d– его диаметр;

g– ускорение силы тяжести;

Архимедова сила находится по уравнению:

(1.6)

где ρ– плотность жидкости,

Сила сопротивления движению, в соответствии с формулой Стокса:

(1.7)

где – динамический коэффициент вязкости жидкости;

– скорость падения шарика.

Выражая величину из уравнений (3) ― (6), получаем:

(1.8)

Если за время t_p шарик проходит расстояние l _p , то:

(1.9)

Формула Стокса (6) справедлива, когда шарик падает в неог­раниченном объеме жидкости. Поправку к формуле Стокса, учитывающую влияние стенок полости, теоретически обосновал Ладенбург. С учетом этой поправки, а такие соотношения (8) получаем:

(1.10)

где D – диаметр цилиндрической полости.

Плотномер-вискозиметр 4 содержит два вертикальных канала, со­общающихся между собой сверху и снизу. В один из каналов с малым зазором помещен груз. В прибор залита жидкость (минеральное масло), плотность и вязкость которой определяются по времени падения груза и перепаду уровней в каналах.

Вискозиметр Оствальда 5 служит для определения вязкости жид­кости (масла) по времени истечения ее из емкости через капилляр.

Рис. 1.1. Схема опытного устройства:

1― термометр; 2― ареометр; 3― вискозиметр Стокса; 4― плотномер-вискозиметр; 5― вискозиметр Оствальда; 6― сталагмометр.

Сталагмометр 6 предназначен для определения поверхностного натяжения жидкости методом отрыва капель. Прибор объединен с вискозиметром 5 общими полостями и содержит емкость с капилляром, расширенная на конце для накопления жидкости в виде капли. Сила поверхностного натяжения при отрыве капель равна их весу, который рассчитывается по плотности жидкости и числу капель, полученному при опорожнении емкости известного объема.

Приборы 3, 4, 5 и 6 приводятся в действие переворотом корпуса устройства, располагаемого в вертикальной плоскости. Характерис­тики всех приборов указаны на корпусе устройства.

Проведение опыта:

1. Подсчитать общее число градусных делений ∆Т в шкале термо­метра 1 и измерить расстояние l _T между крайними штрихами шкалы. Эти результаты занести в таблицу наблюдений 1.1., (характеристики тер­мометра: r - радиус капилляра и W - начальный объем термомет­рической жидкости (при 0° C°)).

2. Измерить ареометром (спиртомером) 2 объемную концентрацию (крепость) водно-спиртового раствора С_с.

3. Перевернуть корпус опытного устройства и измерить секундоме­ром время t_p прохождения шариком расстояния l_p между двумя мет­ками в приборе 3. Опыт провести три раза. Занести в таблицу наблюдений 1.1. среднеарифметическое значение t_p, величину l_p.

4. Медленно повернуть корпус устройства в его плоскости на 180° против часовой стрелки и в приборе 4 измерить перепад уровней масла h и время t_M прохождения грузом расстояния l_M между двумя метками. Записать значения в таблицу наблюдений 1.1.

5. Перевернуть устройство в его плоскости против часовой стрелки и определить время t_в истечения объема жидкости высотой S из емкости капиллярного вискозиметра 5. Повторить опыт не менее трех раз и среднеарифметическое значение времени занести в таблицу наблюдений 1.1. Измерить температуру Т с помощью термометра 1.

6. Повернуть устройство в его плоскости по часовой стрелке, вернув его в исходное положение, и подсчитать число капель, полученных в сталагмометре 6 из объема жидкости высотой S. Повто­рить опыт не менее трех раз и среднеарифметическое значение числа капель П занести в таблицу наблюдений 1.1.

Обработка результатов опыта:

1. Вычислить приращение объема термометрической жидкости, соответствующее повышению ее уровня в капилляре от нижнего до верхнего штриха шкалы:

(1.11)

Влияние расширения баллона и капилляра не учитывается ввиду малости.

По формуле (2) найти значение температурного коэффициента объем­ного расширения β_Т и сравнить его со справочным значением: β^’_T=1,1·10^-3K^-1.

2. Из таблицы 1.1. определить плотность водно-спиртового раствора ρ_c.

Таблица 1.1.

Плотность водно-спиртового раствора (T=20 °C)

Cc	%	0	10	20	30	40	50	60	70	80	90	100
ρc	кг/м3	998	985	974	962	948	930	909	885	859	829	789

3. Вычислить опытное значение динамического коэффициента вязкости водно-глицеринового раствора по формуле (10). Сравнить опытное значение с табличным значением (табл. 1.2 ), рассчитанным методом интерполяции по концентрации раствора С_р, причем:

(1.12)

где ρ_в=998 кг/м³ – плотность воды;

ρ_Г =1260 кг/м³ – плотность глицерина.

Таблица 1.2

Динамический коэффициент вязкости водно-глицеринового раствора (Т=20 °С)

Ср, %	8	21	44	76	94	100
· 103, Па·с	1,3	2,1	6,0	61,8	543,5	1490,0

4. Вычислить значения плотности и кинематического коэффициента вязкости масла "Турбинное 22" по формулам:

(1.13) (1.14)

5. Вычислить значение кинематического коэффициента вязкости трансформаторного масла в приборе 5 по формуле (15) и сравнить его со значением ν′_в, определенным по справочнику.

   (1.15)

6. Определить опытное значение коэффициента поверхностного натя­жения трансформаторного масла по формуле (16) и сравнить его со значением определенным по справочнику.

(1.16)

Результаты всех расчетов внести в таблицу наблюдений 1.1.

Таблица наблюдений 1.1.

∆Т	lT	r	W	∆W	βТ	Β`Т	Cc	ρc	tp	lp
°С	мм	см	мм3	см3	К-1	К-1	%	кг/м3	с	мм
		0,001	257

d	D	ρ	ρш			h	tм	А	В	ρгр
м	м	кг/м3	кг/м3	Па·с	Па·с	мм	с	м-1	м/с2	кг/м3
0,005	0,02	1260	3984					36	77·10-6	2240

ρм	vм	tв	M	νв	T	v`в	n	K
кг/м3	м2/с	с	м2/с2	м2/с	°С	м2/с		м3/с2	H/м	H/м
			18·10-9					11·10-3

Лабораторная работа № 2 измерение гидростатического давления и экспериментальное подтверждение закона паскаля

Цель работы: 1. Измерить с помощью пружинных манометров гидростатическое давление в трёх точках (А, В, С), заглублённых на различную величину под уровень жидкости, находящейся в абсолютном покое под действием силы тяжести;

2. Подтвердить на основании опытных данных закон Паскаля;

3. Построить по данным опыта №2 в масштабе эпюру манометрического давления по глубине .

Теоретическая часть:

Гидростатическое давление это нормальное сжимающее напряжение, возникающее в покоящейся жидкости под действием поверхностных и массовых сил,

, (2.1)

где - элементарная равнодействующая поверхностных сил (гидростатическая сила), Н;

- элементарная площадка действия, м².

Из формулы (1.1) видно, что гидростатическое давление есть предел отношения элементарной гидростатической силы к элементарной площади действия , когда последняя стремиться к нулю.

За единицу гидростатического давления принято равномерно распределённое давление, создаваемое силой в 1 Н, на площади в 1 м², т.е. (один Паскаль).

Гидростатическое давление, отсчитываемое от нуля, называют абсолютным ( ), а отсчитываемое от атмосферного ( ) – избыточным ( ), следовательно

, (2.2)

Очевидно,

. (2.3)

В гидравлических расчётах величину нормального атмосферного давления считают равной =98100 Па.

Из формулы (2.3) видно, что в зависимости от соотношения между и избыточное давление может быть и положительной, и отрицательной величиной. Положительное избыточное давление называют манометрическим, а отрицательное – вакуумметрическим. Приборы, применяемые для измерения + и - , называют соответственно манометрами и вакуумметрами.

По принципу действия манометры и вакуумметры делятся на две группы: жидкостные и механические.

Жидкостный манометр (пьезометр) представляет собой стеклянную трубку, верхний конец которой открыт в атмосферу, а нижний присоединён к точке, где измеряется манометрическое давление.

Манометрическое давление, выраженное через показания манометра, равно:

, (2.4)

где - объемный вес жидкости;

- пьезометрическая высота, т.е. высота, отсчитываемая от точки подключения пьезометра до уровня жидкости в нём.

Действие механических приборов основано на деформации под действием давления упругого элемента (пружины или мембраны). Заметим, что пружинный манометр показывает давление в точки жидкости на уровне оси вращения его стрелки. Если высотное положение оси вращения стрелки и точки подключения манометра не совпадает (рис 2.1), в показание манометра ( ) вводят поправку ( ).

Для случая, изображённого на рис.2.1,

, (2.5)

где - превышение оси вращения стрелки манометра над точкой его подключения, М.

Когда на покоящуюся жидкость действует только сила тяжести, распределение гидростатического давления по глубине (рис. 1.2) описывается основным уравнением гидростатики:

, (2.6)

где - гидростатическое давление в жидкости на глубине , Па;

- внешнее давление, т.е. гидростатическое давление на свободной поверхности жидкости, Па;

- глубина погружения в жидкость рассматриваемой точки, М;

- весовое давление, т.е. гидростатическое давление, создаваемое весом столба жидкости, Па.

Из уравнения (2.6) видно, что при и давление с изменением величины изменяется по линейному закону (см. рис. 2.2). Вычислив по уравнению давление в двух точках, заглублённых на разную величину , можно построить диаграмму распределения гидростатического давления по глубине, называемую эпюрой гидростатического давления (см. рис. 2.2).

Из уравнения (2.6) следует, что внешнее давление в покоящейся жидкости передаётся во все точки её объёма без изменения (см. рис. 2.2). Это следствие, вытекающее из уравнения (2.6), называют законом Паскаля. Справедливость этого закона предстоит проверить опытным путём в данной работе.

Рис.2.1. Схема экспериментальной установки для изучения закона Б.Паскаля

1-циллиндрический резервуар; 2-предохранительный клапан; 4-шкала;5-пьезометр (водомерная трубка); 6-вентиль для сброса избыточного давления; 7-вентиль для подачи сжатого воздуха

Рис 2.2 К закону Паскаля и его экспериментальному подтверждению

В данной лабораторной работе предусмотрено измерение манометрического давления пружинными манометрами.

Описание установки. Установка (см. рис. 2.1) представляет собой толстостенный стальной цилиндр 1, частично заполненный водой, уровень которой измеряется водомерной трубкой 5 со шкалой 4.

Для изменения гидростатического давления над свободной поверхностью жидкости (в т. А) и в точках В и С, заглублённых под уровень соответственно на и , подключены пружинные манометры , , .

В пространство над свободной поверхностью можно подавать сжатый воздух от компрессора (на рис. не показан) по трубопроводу 3 открытием вентиля 7. Для сброса избыточного гидростатического давления в цилиндре служит вентиль 6. В крышке цилиндра имеется предохранительный клапан 2, отрегулированный на давление 500 кПа.

Порядок выполнения работы и обработка опытных данных

Необходимо выполнить два опыта, обеспечив в первом , а во втором - .

Опыт №1. Открыть вентиль 6, для обеспечения , далее, измерить с помощью водомерной трубки 5 и шкалы 4 глубины погружения и точек В и С, а также превышения и осей вращения стрелок манометров и над точками их подключения. Затем измерить показания всех трёх манометров ( , , ). Полученные данные записать в таблицу 2.1 (графы 4 и 6).

Опыт №2. Закрыть вентиль 6, а вентиль 7, открыть. Затем включить компрессор и для подачи сжатого воздуха в цилиндр 1. Довести до величины, указанной преподавателем, после чего компрессор отключить. Далее, измерить одновременно показания манометров . Результаты измерений записать в графу 5 таблицы 1.1. Открыть вентиль 6 для сброса давления сжатого воздуха.

Выполнить все вычисления, предусмотренные таблицей 2.1. Дать заключение по результатам работы.

Основные контрольные вопросы

1. Что такое гидростатическое давление и каковы его свойства?

2. Поясните, что такое абсолютное и избыточное гидростатическое давление и какова связь между ними?

3. Объясните, что понимают под терминами: «внешнее давление» и «весовое давление»?

4. Напишите и поясните основное уравнение гидростатики.

5. Сформулируйте закон Паскаля.

6. Назовите приборы для измерения избыточного гидростатического давления и поясните принцип их действия.

7. Поясните, что такое пьезометрическая высота?

8. В чём состояло принципиальное отличие в условиях проведения первого и второго опытов?

9. Для чего нужно знать превышение оси вращения стрелки пружинного манометра над точкой его подключения?

10. В чем заключается разница между давлением и напором?

Таблица 2.1

№ позиций	Наименования и обозначения измеряемых и вычисляемых величин		Единицы измерения.	Результаты измерений и вычислений		Примечания
				Опыт № 1	Опыт № 2
1	2		3	4	5	6
1	Показания манометров		Па			hc = ……м
			Па
			Па
2	Избыточное гидростатическое давление в точках А, В, С		Па
			Па
			Па
3	Приращение избыточного гидростатического давления		Па
			Па
			Па
4	Средняя величина приращения избыточного гидростатического давления		Па
5	Относительные расхождения приращений давления в точках А, В, С со средней величиной.		-
			-
			-

Лабораторная работа №3 определение опытным путем слагаемых уравнения д. Бернулли.

Цель работы:

1.Определить опытным путем слагаемые z, p/g, U²/2g уравнения Д. Бернулли для сечений I-I…II-II, а также потери полного напора h`_w1-2 между сечениями (см. рис.6).

2. Вычислить средние скорости потока и отвечающие им скоростные напоры U²/2g для указанных живых сечений потока жидкости.

3. Построить в масштабе по опытным данным пьезометрическую линию и линию полного напора (см.рис.3.2).

Теоретическая часть:

Для двух произвольно выбранных живых сечений I-I и II-II струйки реальной жидкости (рис.6) при установившемся движении уравнение Д. Бернулли имеет вид:

(3.1)

Слагаемые, входящие в уравнение (3.1), можно истолковать с геометрической и энергетической точек зрения.

С геометрической точки зрения, слагаемые уравнения (3.2)

являются высотами (напорами) : Z - геометрическая высота (напор),т.е. превышение центра тяжести рассматриваемого поперечного сечения струйки над плоскостью сравнения 0-0, выбираемой произвольно (см. рис.3.1); p/g пьезометрическая высота, т.е. высота подъема жидкости в пьезометре, подключенном к центру тяжести рассматриваемого сечения струйки, отвечающая гидродинамическому давлению р в этой точке; U²/2g - скоростная высота (напор), отвечающая местной скорости U ,т.е. скорости в центре тяжести сечения;

- гидростатический напор;

- полный напор в рассматриваемом сечении струйки;

- потеря полного напора, т.е. часть полного напора, затраченная на преодоление гидравлических сопротивлений между сечениями I-I и II-II.

Рис. 3.1 Диаграмма уравнения Д.Бернулли для струйки реальной жидкости

Рис. 3.2 К измерению скоростного напора v²/2g

С энергетической точки зрения слагаемые уравнения (3.1) представляют собой разновидности удельной энергии а именно:

Z - удельная потенциальная энергия положения жидкости в рассматриваемом сечении струйки;

P/g - удельная потенциальная, энергия. давления;

U²/2g - удельная кинетическая энергия;

- полная удельная энергия;

- удельная потенциальная энергия;

h`_w1-2 - потеря полной удельной энергии струйки, т.е. часть ее, затраченная на преодоление работы сил внутреннего трения, обусловленного вязкостью жидкости.

Удельной энергией называется энергия, приходящаяся на единицу веса жидкости.

Величины слагаемых уравнения (3.1) могут быть определены опытным путем следующим образом:

z - геометрическим нивелированием, или же измерением линейкой

p/g - с помощью пьезометрической трубки (пьезометра);

U²/2g - по разности отметок уровней жидкости в скоростной и пьезометрической трубках, подключенных к рассматриваемой точке живого сечения.

подключенных к сечениям I-I и II-II (см. рис. 3.2)

Скоростная трубка (см. рис. 7) представляет собой трубку, верхний конец которой открыт в атмосферу, а нижний изогнут навстречу скорости и в рассматриваемой сечения струйки

( рис. 3.2)

h`_w1-2 - по разности отметок уровней воды в скоростных трубках, точке потока жидкости. Благодаря этому у входа в изогнутый конец скоростной трубки кинетическая энергия частицы жидкости преобразуется в потенциальную энергию давления столба жидкости высотой h_u=U²/2g.

Поскольку срез нижнего конца скоростной трубки перпендикулярен вектору скорости, а срез нижнего конца пьезометра параллелен (см. рис.3.2), уровень жидкости в скоростной трубке всегда устанавливается выше, чем в пьезометре, на величину U²/2g.

Прибор, объединяющий конструктивно пьезометрическую (п) и скоростную (с) трубки, называется трубкой Пито и широко применяется для измерения скорости движения жидкости

.

Для двух сечений потока реальной жидкости уравнение д. Бернулли имеет вид:

, (3.2)

где скоростной напор, отвечающий средней скорости потока жидкости в рассматриваемом живом сечении (здесь Q, - расход потока жидкости,  - площадь живого сечения потока);

h_w1-2 - потеря полного напора (полной удельной энергии) на преодоление работы сил внутреннего и внешнего трения на пути между живыми сечениями потока жидкости I-I и II-II;

 - коэффициент Кориолиса (корректив кинетической энергии), учитывающий неравномерность распределения местных скоростей по живому сечению потока, обусловленную вязкостью жидкости.

Величина  зависит от режима течения жидкости, а также от вида движения. Так, при равномерном движении для ламинарного режима =2,0, а для турбулентного - =1,05…1,15.

Слагаемые уравнений (3.1) и (3.2) в различных живых сечениях можно изображать графически в виде диаграммы уравнения Д. Бернулли (графика напоров), см. рис.1.5, дающей наглядное представление о перераспределении по пути движения жидкости потенциальной и кинетической энергии, а также о характере убывания полной энергии.

3.Описание установки. Установка (рис.3.3) представляют собой трубопровод 2 переменного сечения с напорным баком 1, вода в который подается по питающему трубопроводу 8 открытием вентиля 9. Бак 1 снабжен переливным устройством 10 для поддержания уровня воды на постоянной отметке, чтобы обеспечить в трубопроводе 2 установившееся движение жидкости. К сечениям I-I…II-II трубопровода 2 подключены пьезометры 3 и скоростные трубки 4 для измерения величин p/g и U²/2g. Величина расхода воды в трубопроводе 2 регулируется вентилем 5. Для измерения расхода воды имеются мерный бак 6 и секундомер 7.

3. Порядок выполнения работы и обработка опытных данных.

1. При закрытом вентиле 5 открыть вентиль 9 для заполнения бака 1 и трубопровода 2 водой. При этом следует обратить внимание на уровни воды в пьезометрических 3 и скоростных трубках 4. Эти уровни при отсутствии воздуха в системе должны быть на одной отметке.

2. Открыть вентиль 5 так, чтобы трубопровод 2 работал полным сечением, а уровень воды в баке постоянным.

3. Измерить с помощью бака 6 и секундомера 7 расход воды. Затем линейкой измерить геометрические высоты z центров тяжести сечений I-I…II-II относительно плоскости сравнения 0-0, отмеченной на установке.

4. Далее, определить по шкалам отметки уровней воды в пьезометрах и скоростных трубках в сечениях I-I…II-II. Результаты всех измерений записать в таблицу 3.1. Затем выполнить все вычисления, предусмотренные табл. 3.1, и построить в масштабе по полученным данным линии полного напора и пьезометрическую, так, как показано на рис. 3.1.

5. Дать заключение по результатам работы.

4.Основные контрольные вопросы

1. Поясните геометрический смысл слагаемых уравнения Д. Бернулли.

2. Поясните энергетический смысл слагаемых уравнения Д. Бернулли.

3. Как называется коэффициент , входящий в уравнение Д. Бернулли для потока реальной жидкости, что он учитывает и от чего зависит его величина?

4. Объясните, что обусловлены потери полного напора и каков их энергетический смысл?

5. Поясните, что понимают под термином "удельная энергия"?

6. Объясните термины "местная скорость" и "средняя скорость" и укажите, как определяют эти скорости?

7. Поясните, что такое скоростная трубка и трубка Пито?

8. Поясните, что такое линия полного напора и пьезометрическая линия, что будут представлять собой эти линии при равномерном движении реальной жидкости?

9. Что понимают под термином «живое сечение потока жидкости»?

5. Результаты измерений и вычислений

Таблица 3.1.

№ позиции.	Наименование измеряемых и вычисляемых величин	Единицы измерения	Результаты измерений и вычислений
			Сеч. I-I	Сеч. II-II	Сеч. III-III
1	2	3	4	5	6
2	Геометрические высоты центров тяжести сечений, z	м
3	Отметки уровней воды в пьезометрах, т.е. гидростатические напоры (z+p/g)	м
4	Отметки уровней воды в скоростных трубках, т.е. полные напоры H= z + P/g + U2/2g,	м
5	Пьезометрические высоты (z + P/g ) –z,	м
6	Скоростные высоты U2/2g=H-(z + P/g)
7	Потери полного напора на пути между соседними живыми сечениями: h`i-(i+1)=Hi – Hi+1	м
8	Суммарные потери полного напора: h`I-III= HI - HIII	м
9	Объем воды в мерном баке: W,	м3
10	Время наполнения мерного объема: t,	сек
11	Расход воды в трубопроводе: Q=W/t,	м
12	Средняя скорость в сечении: V = Q/S,	м/с
13	Скоростная высота, по средней скорости V2/2g	м
14	Сравнение скоростных высот по трубке Пито и по средней в сечении: (U2/2g – V2/2g)х100/ V2/2g	%

Примечание к табл. 1.

1. Для сечения III-III (см графу 6) числовые значения величин (см.

позиции 5 и 8…13) те же, что и для сечения II-II

2. Потери полного напора h`_w (см. позицию 6) между сечениями II-II и III-III принять равными потерям напора между сечениями I-I и II-II

3. Остальные величины для сеч. III-III (см. позиции 1…4) следует определить с привлечением уравнения Д. Бернулли (см. уравнение 1.11)

Лабораторная работа №4

ЭКСПЕРИМЕНТАЛЬНАЯ ИЛЛЮСТРАЦИЯ ЛАМИНАРНОГО И ТУРБУЛЕНТНОГО РЕЖИМОВ ДВИЖЕНИЯ ЖИДКОСТИ, ОПРЕДЕЛЕНИЕ ЗАКОНОВ СОПРОТИВЛЕНИЯ И КРИТИЧЕСКОГО ЧИСЛА РЕЙНОЛЬДСА.

Цель работы.1. Убедиться на опыте путем окрашивания струйки воды в стеклянной трубе в существовании ламинарного и турбулентного режимов.

2. Вычислить по данным опытов, проведенных на этой трубе, числа Рейнольдса при ламинарном и турбулентною режимах, сравнить их с критическим, убедиться, что при ламинарном режиме Rе< Re_кр , а при турбулентном – Re > Re_кр.

3. Построить по опытным данным, полученным на винипластовой трубе, график lgh_e=f(lg ), определить с его помощью критическую скорость _кр, а через нее вычислить критическое число Re_кр=2320.

2. Подтвердить с помощью графика lgh_e=f(lg ), что при ламинарном режиме потери напора по длине h_e пропорциональны средней скорости в первой степени, а при турбулентном - в степени 1,75  m  2.

Теретическая часть. Многочисленными экспериментальными исследованиями установлено, что движение жидкости может происходить или при ламинарном, или при турбулентном режиме.

Ламинарный режим наблюдается при небольших скоростях движения. При этом окрашенные струйки жидкости не перемешиваются, сохраняясь по всей длине потока, т.е. движение жидкости при ламинарном режиме является струйчатым, перемешивание частиц жидкости отсутствует.

Турбулентный режим наблюдается при значительных скоростях и характеризуется интенсивным перемешиванием частиц жидкости, что обуславливает пульсацию скоростей и давления,

Средняя скорость потока, при которой происходит смена режима движения жидкости, называется критической ( _кр). Величина ее, как показывают опыты в трубопроводах круглого сечения, зависит от рода жидкости, характеризуемого динамической вязкостью , и плотностью, а также от диаметра трубопровода d. Одновременно опытами установлено, что величина безразмерного алгебраического комплекса, отвечающей критической скорости _кр,

(4.1)

от ,  и d не зависит. Re_кр(d)=2320 называется критическим числом Рейнольдса. Устойчивый ламинарный режим наблюдается при значениях числа Рейнольдса , а турбулентный – при

Re_(d)>Re_кр(d).

Таким образом, число Рейнольдса

(4.2)

является критерием, позволяющим судить о режиме движения жидкости в круглой трубе, работающей полным сечением.

Величину =/, входящую в формулу (4.1) и (4.2), называют кинематическим коэффициентом вязкости жидкости.

Рис. 4.1 График зависимости потерь напора по длине h_l от средней скорости v в логарифмической форме

Из изложенного следует, что для определения режима движения жидкости в круглом трубопроводе при напорном движении достаточно вычислить по формуле (4.2) число Рейнольдса и сравнить его с критическим.

Знание режима, движения жидкости необходимо для правильной оценки потерь напора при гидравлических расчетах. Дело в том, что, как показывают опыты в круглых трубах при напорном равномерном движении (результаты их представлены на рис. 9. в виде графика зависимости потерь напора по длине h_e от средней скорости )

При ламинарном режиме потери напора h_e пропорциональны средней скорости в первой степени, а при турбулентном - в степени 1,75 <m>2,0. Заметим, что с помощью этого графика определяют величину критической скорости _кр, а через нее - и критическое число Рейнольдса по формуле (4.1).

Описание установки (рис 4.2.) включает в себя две расположенные горизонтально трубы: стеклянную 1 (d=1,6 cм) и винипластовую 2 (d=0,9 см), в которых и изучается движение воды при различных режимах, напорный бак 3, емкость 11 с раствором красителя, подаваемого открытием краника 10 по трубке 9 во входное сечение трубы 1. Для измерения расхода воды в трубах 1 и 2 служат мерная емкость 16 и секундомер 15.

Вода в напорный бак 3 подается по питающему трубопроводу 4 открытием вентиля 5 из резервуара лаборатории. Для поддержания уровня воды в баке 3 во время опытов на постоянной отметке имеется переливное устройство 6, для контроля за уровнем воды служит электрический уровнемер 7 со световой сигнализацией.

Рис. 4.2 Схема устройства для изучения режимов движения жидкости

Температура воды в баке 3 измеряется термометром 8. Регулирование расхода воды, а следовательно и средней скорости ее движения в трубах 1 и 2, осуществляется кранами соответственно 14 и 13. На винипластовой трубе 2 имеются пьезометры 12 для определения потерь напора по длине h_e (по разности их показаний).

Порядок выполнения работ и обработка опытных данных

1. Открыть вентиль 5 на трубопроводе 4 и наполнить водой бак 3 настолько, чтобы переливное устройство 6 начало работать, после чего вентиль 5 прикрыть.

2. Открыть незначительно кран 14 на стеклянной трубе 1 ,чтобы скорость движения воды в ней была небольшой (вода из трубы 1 должна течь тонкой струйкой).

3. Приоткрыть краник 10 на трубке 9 и подать из емкости 11 в трубу 1 небольшое количество раствора красителя, чтобы окрашенная струйка воды представляла собой отчетливо выраженную нить по всей длине трубы.

4. Измерять о помощью мерного сосуда 16 и секундомера 15 расход воды Q в трубе. При этом измеряемый объем воды в сосуде 16 должен быть также, чтобы время наполнения составляло не менее 20…30 секунд.

5. Измерить температуру воды в баке 3 термометром 8.

6. Результаты измерений записать в табл.4.1.

7. Увеличить открытием крана 14 скорость движения воды в трубе 1, но так, чтобы окрашенная струйка жидкости сохранялась, т.е. чтобы режим остался ламинарным, и выполнив те же измерения, что и в первом опыте, записать их результаты в табл.4.1.

8. Дальнейшим увеличением открытия крана 14 создать в трубе 1 турбулентный режим (об этом будет свидетельствовать интенсивное перемешивание с водой раствора красителя, подачу которого следует увеличить, чтобы эффект был ярче) и выполнить третий и четвертый опыты так, как описано выше. После чего закрыть краник 10 и кран 14. Результаты измерений записать в табл.1.4.

9. Открыть кран 13 на винипластовой трубе 2 так, чтобы разность показаний пьезометров 12 составляла не более 0,3 см и измерить расход воды и ее температуру. Результаты измерений записать в табл.1.5.

10. Сделать ещё девять аналогичных опытов, увеличивая в каждом после дующем опыте открытие крана 13 так, чтобы разность показаний пьезометров 12 (потеря напора по длине ) при этом возрастала примерно в 1,5…1,6 раза. Результаты измерений записать в таблицу 1.5.

11. Выполнить все вычисления, предусмотренные таблицами 1.4 и 1.5.

1. Построить в масштабе по данным таблицы 1.5 график (см. рис. 1.8) и определить с его помощью критическую скорость , а через неё и , а также показатели степени и и коэффициенты пропорциональности и .

1. Назовите режимы движения жидкости и укажите их характерные особенности.

2. Поясните, что такое критерий Рейнольдса, и назовите факторы, от которых он зависит.

3. Поясните, что такое критическое число Рейнольдса?

4. Поясните, каким образом при гидравлических расчётах определяют режим движения жидкости и, с какой целью?

5. Поясните, что такое критическая скорость, от каких факторов она зависит и как её определяют?

6. Напишите и поясните аналитические зависимости потерь напора по длине от средней скорости потока при ламинарном и турбулентном режимах движения жидкости.

7. Изобразите график зависимости потерь напора по длине от средней скорости ( в логарифмических координатах) и дайте пояснения к нему.

Таблица 4.1.

Основные расчетные формулы.

№ позиций	Наименование и обозначения измеряемых и вычисляемых величин	Ед. изм.	Рез. измерений и вычислений
			Ламин. режим		Турбул. режим
			Опыт 1	Опыт 2	Опыт 3	Опыт 4
1	2	3	4	5	6	7
1	Объём воды в мерном сосуде	см3
2	Время наполнения объёма	с
3	Расход воды	см3/с
4	Внутренний диаметр стеклянной трубы	см
5	Площадь попереч. сечения трубы	см2
6	Средняя скорость движения воды	см/с
7	Температура воды
8	Кинематический коэффициент вязкости воды (по справочнику)	см2/с
9	Число Рейнольдса	-
10	Критическое число (по справочнику)	-

Таблица 4.2.

№ позиций	Наименование и обозначения измеряемых и вычисляемых величин	Ед. изм.	Результаты измерений и вычислений
			Номера опытов
			1	2	3	4	5	6	7	8	9	10
1	2	3	4	5	6	7	8	9	10	11	12	13
1	Объём воды в мерном сосуде	см3
2	Время наполнения	с
3	Расход воды	см3/с
4	Внутренний диаметр трубы	см
5	Площадь попереч. сечения трубы	см2
6	Средняя скорость потока	см/с
7	Логарифм средней скорости	-
8	Отметка уровня воды в пьезометре 1,	см
9	Отметка уровня воды в пъезометре	см
10	Потеря напора по длине	см
11	Логарифм потерь напора по длине	-
12	Температура воды
13	Кинематический коэффициент вязкости воды (по справочнику)	см2/с

Лабораторная работа №5 изучение гидравлических потерь по длине трубопровода и в местных сопротивлениях.

Цель работы: 1. Определить по опытным данным, воспользовавшись формулами (5.1) и (5.3), значение коэффициента гидравлического трения и величины коэффициента для трех видов местных сопротивлений;

2. Установить, воспользовавшись соотношениями А.Н. Альтшуля или же графиком Никурадзе (см. рис. 5.1) области гидравлического сопротивления, в которых работали участки напорного трубопровода;

3. Вычислить значения коэффициентов гидравлического трения по соответствующим эмпирическим формулам;

1. Найти справочные значения коэффициентов местных сопротивлений ( по таблице, и вычислить по формулам (5.4), (5.6));

Теоретическая часть. Экспериментальными исследованиями установлено, что при движении жидкости часть полного напора ( энергии) затрачивается на преодоление работы вязкостных и инерционных сил, т.е. возникают потери напора.

При равномерном движении жидкости гидравлическое сопротивление, проявляющееся равномерно по всей длине потока, называют сопротивлением по длине, а вызываемые им потери напора , - потерями напора по длине (h_l). Эти потери в круглых трубопроводах, работающих полным сечением, вычисляют по формуле Дарси-Вейсбаха:

(5.1)

где l - безразмерный коэффициент, называемый коэффициентом гидравлического трения (коэффициентом Дарси). Величина коэффициента l характеризует гидравлическое сопротивление трубопровода и зависит в общем случае от числа Рейнольдса Re и относительной шероховатости D_э/d трубопровода, т.е. l=f(R_e, D_э/d);

l, d – длина и внутренний диаметр трубопровода;

– средняя скорость движения потока жидкости.

Величину коэффициента l при гидравлических экспериментах вычисляют по опытным данным из формулы (1.15). При гидравлических же расчетах – по эмпирическим и полуэмпирическим формулам, например, при ламинарном режиме l_п=64/R_е, а при турбулентном режиме движения и работе трубопровода в области доквадратичного сопротивления – по формуле А.Д. Альтшуля:

(5.2)

Величину абсолютной эквивалентной шероховатости D_э при расчетах берут из справочной литературы в зависимости от материала трубопровода и состояния его внутренней поверхности. Например, для труб из органического стекла D_э=0,006 мм, а для стальных водопроводных умеренно заржавленных труб D_э=0,20…0,50 мм.

Область гидравлического сопротивления при расчетах определяют или непосредственно по графикам l=f(Re,D_э/d), полученным опытным путем для труб из различных материалов и приведенным в справочной литературе, например, по графику Никурадзе (рис. 1.10), или же с помощью соотношений и , предложенных А. Д. Альтшулем на основе использования упомянутых графиков. В последнем случае поступают следующим образом.

Вычисляют соотношения 10d/Dэ и 500d/Dэ и сравнивают их с числом Рейнольдса Re = Vd/n. При этом, если, , трубопровод работает в области гидравлически гладких труб. Если , трубопровод работает в области квадратичного сопротивления. Если же 10d/Dэ < Re > 500d_э/Dэ, трубопровод работает в области доквадратичного сопротивления.

Следует иметь в виду, что для каждой области гидравлического сопротивления предложены и используются при гидравлических расчетах свои формулы для вычисления коэффициента l.

Другой вид гидравлических сопротивлений, возникающих в местах резкого изменения конфигурации потока, называют местным сопротивлениями, а вызываемые ими потери напора, - местными потерями напора (h_м).

При прохождении через любое местное сопротивление поток жидкости деформируется (рис.11 а,б,в), вследствии чего движение становится неравномерным резко изменяющимся, для которого характерны :

а) значительное искривления линий потока и кривых сечений

потока;

б) отрывы транзитной струи от стенок трубопровода (ввиду

действия закона инерции) и возникновения в местах отрыва

устойчивых водовязатов;

в) повышенная (по сравнению с равномерным движением)

пульсация скоростей и давлений;

г) изменение формы ( переформирование ) эпюр скоростей.

Местные потери напора при гидравлических расчетах вычисляют по формуле Вейсбаха :

, (5.3)

где - безразмерный коэффициент, называемый коэффициентом местного сопротивления;

- средняя скорость потока в сечении за местным сопротивлением, т.е. ниже по течению (если скорость , как исключение, принимается перед местным сопротивлением, это обязательно оговаривается).

Величина коэффициента зависит в общем случае от числа Рейнольдса и от конфигурации, т.е. формы проточной части местного сопротивления. В частном случае, когда трубопровод, на котором расположено местное сопротивление, работает в области квадратичного сопротивления, величина коэффициента от не зависит.

Величину для каждого вида местного сопротивления определяют по данным гидравлических экспериментов, пользуясь формулой (1.3). полученные таким образом значения коэффициентов для различных видов местных сопротивлений (обычно при квадратичной области сопротивления) приводятся в справочной и специальной литературе, откуда и берутся при гидравлических расчётах. Исключением является резкое расширение и резкое сужение трубопровода (см. рис. 11 а, б), для которых численные значения координаты определяются по формулам, полученным теоретически. Так, при резком расширении трубопровода, когда средняя скорость в формуле (1.3) взята перед местным сопротивлением, т.е. ,

, (5.4)

если же скорость берется за местным сопротивлением, т.е. , (5.5)

Коэффициент сопротивления при резком сужении трубопровода ( ) принято относить к скорости после сужения. При этом

, (5.6)

где - коэффициент сжатия струи.

Рис. 5.1. график зависимости коэффициента гидравлического трения l

от числа Рейнольдса Re для труб с различной относительной шероховатостью D/d (график Никурадзе)

Рис. 5.2. Схемы движения жидкости при резком (внезапном) изменении сечения трубопровода:

а) резкое расширение трубопровода;

б) резкое сужение трубопровода

Рис. 5.3. Схема установки для изучения гидравлических сопротивлений (по длине и местных) в напорном трубопроводе круглового сечения

Цель работы: 1. Определить по опытным данным, воспользовавшись формулами (5.1) и (5.3), значение коэффициента гидравлического трения и величины коэффициента для трех видов местных сопротивлений;

2. Установить, воспользовавшись соотношениями А.Н. Альтшуля или же графиком Никурадзе (см. рис. 5.1) области гидравлического сопротивления, в которых работали участки напорного трубопровода;

3. Вычислить значения коэффициентов гидравлического трения по соответствующим эмпирическим формулам;

2. Найти справочные значения коэффициентов местных сопротивлений ( по таблице, и вычислить по формулам (5.4), (5.6));

5. Оценить сходимость и с их расчетными справочными значениями.

2.Описание установки. Установка (рис. 5.2) представляет собой систему напорных трубопроводов с последовательно расположенными на нем гидравлическими сопротивлениями (по длине и местными). К каждому гидравлическому сопротивлению подключено по два пьезометра (перед и за ним). Все пьезометры для удобства работы выведены на щит 4. Для регулирования расхода воды в системе служит вентиль 2. Величина измеряется с помощью мерного бака 1 и секундомера. 3. Подача воды в систему осуществляется из питающего резервуара 5 по трубе 7 открытием задвижки 6. Постоянный уровень воды в резервуаре 5 ( для обеспечения установившегося движения в системе) поддерживается переливным устройством. Вода в резервуар 5 подается центробежным насосом.

3.Порядок выполнение работы и обработка опытных данных.

При закрытом вентиле 2 и задвижке 6 включить насос и обеспечить подачу воды в питающий резервуар 5. После наполнения водой резервуара и стабилизации уровня воды в нем ( переливное устройство должно при этом работать) следует плавным открытием вентиля 2 подать воду в систему трубопроводов. Далее, необходимо измерить: отметки уровней воды в пьезометрах, расход воды в системе ( с помощью мерного бака 1 и секундомера 3), а так же ее температуру (термометром в резервуаре 1). Результаты измерений для двух опытов (при разных расходах воды) записать в таблицу 5.1.

Обработать опытные данные и результаты представить в виде таблицы 1.7. Сформировать выводы по результатам работы.

4.Основные контрольные вопросы.

1. Напишите и поясните формулы Дарси-Вейсбаха и Вейсбаха.

2. Поясните, как опытным путем определяют величины коэффициентов l и x.

3. Что характеризуют коэффициенты l и x от каких факторов в общем случае они зависят и как их определяют при гидравлических расчетах?

4. Объясните, что такое D_э и D_э/d, как найти величину D_э при гидравлических расчетах.

5. Назовите области гидравлического сопротивления трубопроводов и объясните, как определяют область сопротивления при гидравлических расчетах.

6. Изобразите схемы движения жидкости при резком повороте трубы на 90⁰, а также при резком расширении и резком сужении трубопровода и дайте пояснения к ним, указав, что характерно для движения потока при протекании его через любое местное сопротивление.

Таблица 1.7

№ поз.	Наименование и обозначения измеряемых величин		Ед. изм.	Результаты вычислений
				Потери по длине				Местные сопротивления
				Участок 1		Участок 2		Резкий поворот		Резкое сужение		Резкое расшире-ние
1	Номера сечений
2	Диаметр трубы в сечении		м
3	Площадь поперечном сечения трубы		м2
4	Отметка пьезометра в сечении, Z + P/ρ g		м
5	Объем воды в мерном баке, W		м3
6	Время наполнения мерного объема, t
8	Расход воды		м3/с
9	Средняя скорость потока		м/с
10	Скоростной напор		м
11	Потери напора по длине и местные (по разности полных напоров перед и за сопротивлением)		м
12	Расстояния между точками подключения пьезометров (длины участков), L		м
13	Коэффициент гидравлического трения по опытным данным		-
14	Коэффициент местного сопротивления по опытным данным		-
15	Кинематический коэффициент вязкости воды (по справочнику)		м2/с
16	Число Рейнольдса		-
17	Область гидравлического сопротивления (гладких труб, доквадратич., квадратич.)		-
18	Коэффициент гидравлического трения по эмпирическим формулам		-
19	Коэффициент местного сопротивления (по справочнику и теоретическим формулам)		-		-
20	Относительное отклонение и		-
			-

Лабораторная работа № 6 определение величины гидравлического удара в трубопроводе

Гидравлическим ударом называется изменение давления в напорном тру­бопроводе, вызванное резким изменением скорости движения жидкости. При быстром (практически мгновенном) закрытии крана на трубопроводе возни­кает прямой положительный удар, величина которого h_уд определяется (сверх статистического) по формуле профессора Н.Е. Жуковского:

_(6.1)

_(6.2)

где С - скорость распространения волны удара, м/с;

и - скорости движения воды в трубопроводе после удара и до удара, м/с;

- толщина стенок трубопровода, м;

Е_воды и Е_стали - модули объемной упругости воды и стали, кгс/м²;

1425 м/с - скорость распространения звука в покоящейся воде.

Цель работы:

Определить в опыте величину гидравлического удара и сравнить ее с ве­личиной удара, подсчитанной по формуле профессора Н.Е. Жуковского Схема опытной установки:

Е_СТАЛИ =2,1*10⁶кгс/см²

Е_ВОДЫ =2,1*10⁴кгс/см²

м/с

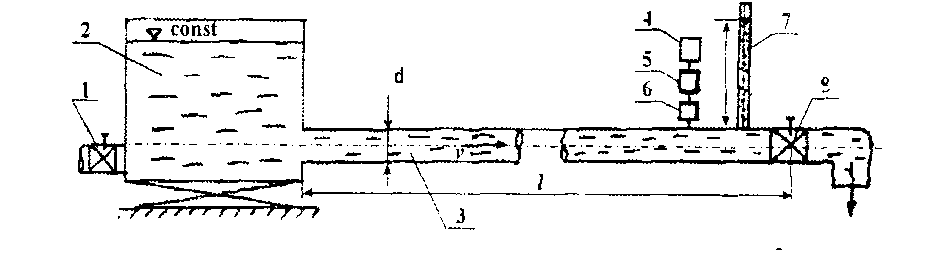
Рис. 6.1. Установка для измерения гидравлического удара

Ход работы

1. Открывается кран 1 и расход воды подается в бак постоянного напора 2. кран 8 закрыт.

2. По пьезометру 7 устанавливается Н_ст, - статический напор.

3. Открывается полностью пробковый кран 8, дается время для достиже­ния установившегося движения в напорной системе.

4. Подставляется мерный сосуд под струю жидкости крана 8 и синхронно включая секундомер, фиксируется объем воды W и время наполнения t, no которым можно определить опытный расход, м³ /с.

_(6.3)

5. Трехходовым краном 6 удаляется воздух перед тензодатчиком 5.

6. Подается электропитание на тензодатчик и регистрирующий прибор 4

7. Включается регистрирующий прибор 4. В течение непродолжительно­го времени (5... 10 с) он фиксирует на бумаге рабочее давление в трубопро­воде, после чего мгновенно закрывается кран 8, а регистрирующий прибор фиксирует повышение давления в трубопроводе в результате удара.

8. Выключается регистрирующий прибор, отключается электропитание, закрывается кран 1 и обрывается кран 8 для опорожнения системы. Все опытные и расчетные данные заносятся в таблицу.

Таблица 6.1 Опытных данных и результатов вычислений

W (м3)	t(c)	Q (м3 /с)	hуд.оп. (м)	Нст(м)	С (м/с)	hуд.расч (м) '
						|

Контрольные вопросы

1. Дайте определение гидравлического удара.

2. Охарактеризуйте зону упругой деформации.

3. Приведите зависимость для определения величины гидравлического удара.

4. Приведите зависимость для определения скорости распространения гидравлического удара.

5. Охарактеризуйте полный гидравлический удар.

6 Охарактеризуйте неполный гидравлический удар.

7. Профилактика гидравлического удара.

8. Опишите опытную установку.

9. Перечислите пункты выполнения работы

ПРИЛОЖЕНИЯ

ПРИЛОЖЕНИЕ 1

Некоторые физические свойства жидкостей при давлении 0,1 МПа

Жидкость			Температура, 0С	Плотность, кг/м3	Удельный вес, Н/м3	Вязкость 104,м2/с
Бензин	авиационный		20	739-780	7250-7652	0,49 для 20 0С
	автомобильный			712-761	6980-7470
Масло	веретенное АУ (ГОСТ 1642-75)		50	888-896	8711-8790
	для гидравлических систем АМГ-30 (ГОСТ 6794-75)			850	8340
	индустриальное общего назначения без присадок (ГОСТ 20799-75)	И-5А		890	8731	0,04-0,06
		И-8А		900	8829	0,06-0,08
		И-12А		880	8633	0,10-0,14
		И-20А		885	8682	-
		И-25А		890	8731	0,24-0,27
		И-30А		890	8731	0,28-0,33
		И-40А		895	8780	0,35-0,45
		И--100А		920	9025	0,90-1,18
	соляровое		20	885-902	8680-8850
	трансформаторное		50	886	8692
	турбинное (ГОСТ 32-74)	22		900	8829
		30		900	8829	0,28-0,36
		46		900	8829	0,44-0,48

 

ПРИЛОЖЕНИЕ 2

Кинематическая вязкость масел при различных температурах

Масло			104, м2/с при 0С
			100	50	10	0	-5	-10
веретенное АУ (ГОСТ 1642-75)			0,036	0,13	0,90	1,80	2,80	4,40
для гидравлических систем АМГ-30 (ГОСТ 6794-75)			0,047	0,11	0,30	0,44	0,54	0,67
индустриальное (ГОСТ 20799-75)		И-20	0,048	0,18	1,13	2,75	4,20	6,40
		И-45	0,081	0,42	5,01	11,90	19,50	59,90
		И-50 (машинное СУ)	0,085	0,50	8,33	22,90	41,70	83,80
трансформаторное с присадкой ионол			0,030	0,09	0,05	0,89	1,24	1,77
турбинное (ГОСТ 32-74; 9972-74)	ТП-22		0,060	0,22	2,13	4,76	7,73	9,10
	ТП-22 (из сернистых нефтей)		0,050	0,21	1,72	3,75	5,68	25,30
	ТП-30УТ		0,060	0,42	3,59	8,63	14,40	33,10

 

ПРИЛОЖЕНИЕ 3

Динамическая вязкость масел при различных температурах

Жидкость	0C	10-1 Па с при давлении МПа
		0,1	10	20	30	40	50
Автол	37	1,440	1,940	2,450	3,030	3,672	4,896
Машинное	22	2,880	3,416	4,176	5,184	6,822	8,640
Трансформаторное	22	0,346	0,374	0,418	0,489	0,562	0,650

Литература.

1. Гидравлика, гидромашины и гидроприводы: Учебник для машиностроительных вузов/ Т.М. Башта, С.С. Руднев и др. - М.: Машиностроение, 1982.

2. Справочное пособие по гидравлике, гидромашинам и гидроприводам. Под общей редакцией Б.Б. Некрасова. -Мн.: Высш.шк., 1985.

3. Гидравлика, гидромашины и гидропневмопривод. / Стесин С.П., ред. - А: Академия., 2005 г.

4. Гидравлика и гидропневмопривод: Ч.1: основы механики жидкости и газа: учеб. Пособие./ Шейпак А.А., Издательство: МГИУ (Москва, 2003).

5. Альтшуль А.Д. Гидравлические сопротивления. - М.: Недра, 1982.-224 с.

Учебное издание

Составители:

Котомчин А.Н.

Клинк Г.В.

Гидравлика

Методические указания к выполнению лабораторных работ по курсу по дисциплине "Гидравлика" специальности 110301 «Механизация сельского хозяйства», 110302 «Электрификация и автоматизация», 110303 «Механизация переработки сельскохозяйственной продукции»

В авторской редакции

Компьютерный набор И.А. Дубовая

Компьютерная вёрстка А.Н. Котомчин

Сдано в набор «__»________2012

Подписано в печать «__»_______2012

Формат 60х90/16____

Уч.-изд. л. 3,0. Тираж 50 экз.

Изд-во Приднестр. ун-та 3300, Тирасполь, ул. 25 Октября 128.

62

61

60

59

58

3

4

57

5

56

6

55

54

7

8

53

52

9

10

51

50

11

12

49

48

13

14

47

46

15

16

45

44

17

18

43

42

19

20

41

40

21

22

39

38

23

24

37

36

25

26

35

34

27

28

33

32

29

30

31