24.Огранниченность ф-циинепрер. На отрезке.

Определение 1. Функция f(x) непрерывная во всех точках некоторого множества X, называется непрерывной на этоммножестве.Если X = [a; b], то для непрерывности функции на X требуется, чтобы f(x) была непрерывна во всех внутреннихточках отрезка, непрерывна справа на левом его конце, т.е. в точке a, и непрерывна слева на правом его конце, т.е. вточке b.

Т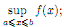 еорема 4 (Вейерштрасса).Всякая непрерывная на отрезке функция ограничена и достигает на нем своих верхнейи нижней граней.

Доказательство. Пусть функция f(x)

на отрезке [a; b] и пусть M =M как и всякая верхняягрань непустого множества чисел, может быть либо конечной, либо бесконечной, равной + . Покажем, что M < + и что существует такая точка x0 ∈ [a; b], что f(x0) = M.Выберем какую-либо последовательность таких чисел a_n, n = 1, 2, . . ., что a_n = M, an< M, n = 1, 2, . . (1) Согласно определению верней грани функции для каждого a_n, n = 1, 2, . . . существует такая точка x_n∈ [a; b], что f(x_n) >a_n, n = 1, 2, . . . (2). С другой стороны, поскольку M верхняя грань функции f(x), для всех точек x∈ [a; b] справедливо неравенство f(x) M.(3) Последовательность {x_n} ограничена, так как a x_n b, n = 1, 2, . . ., поэтому по теореме Больцано-Вейерштрасса из нее можно выделить сходящуюся последовательность {x_nk}, и пусть x_nk=x₀. Так как a x_nk b, то a x₀ b. Из неравенств (2) и (3) следует, что a_nk< f(x_nk ) M, k = 1, 2, . . . (4). С другой стороны, в силу непрерывности функции f(x) на отрезке [a; b] она непрерывна в точке x₀ этого отрезка и,

следовательно f(x_nk)=f(x₀).т.е. имеем M = f(x₀).

Таким образом, доказано, что верхняя грань M функции f(x) совпадает со значением функции в точке x₀ и, следовательно, конечна. Тем самым функция f(x) ограничена сверху и ее верхняя грань достигается в точке x0 ∈ [a; b].

Аналогично доказывается, что непрерывная на отрезке функция ограничена снизу и достигает на нем своей нижней грани.

25. Промежуточные значения непрерывных функций.

Теорема 5 (Больцано-Коши). Если функция f(x) непрерывна на отрезке [a; b] и f(a) = A, f(b) = B, то для любого C,заключенного между A и B, существует такая точка ξ ∈ [a; b], что f(ξ) = C.Доказательство. Пусть для определенности f(a) = A < B = f(b) и A < C < B. Разделим отрезок [a; b] точкой x0 надва равных по длине отрезка; тогда либо f(x₀) = C и, значит, искомая точка ξ = x₀ найдена, либо f(x₀) C и тогдана концах одного из полученных отрезков функция f(x) принимает значения, лежащие по разные стороны от числа C,точнее - на левом конце значение меньшее C, на правом - большее.Обозначим этот отрезок [a₁; b₁] и разделим его снова на два равных по длине отрезка и т.д. В результате либо черезконечное число шагов придем к искомой точке ξ, в которой f(ξ) = C, либо получим последовательность вложенныхотрезков [a_n, b_n], по длине стремящихся к нулю и таких, чтоf(a_n) < C < f(b_n). (1)

Пусть ξ - общая точка всех отрезков [an; bn], n = 1, 2, . . . Как известно ξ = _n= b_n. Поэтому, в силу непрерывности функции можем записать f(ξ) = _n)= (b_n)

Тогда из (1) _n) C (b_n).т.е. f(ξ) = C.

Следствие 1. Если функция непрерывна на отрезке и на его концах принимает значения разного знака, то на этом отрезке существует хотя бы одна точка, в которой функция обращается в нуль.

Следствие 2. Пусть функция f(x) непрерывна на отрезке

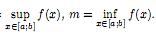[ a; b] и M =

Тогда функция f(x)принимает все значения из отрезка [m;M] и только эти значения.

Доказательство. Заметим, что если

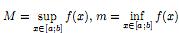
то m f(x) M, и согласно теореме 4, существуют такие точки α ∈ [a; b] и β ∈ [a; b], что f(α) = m, f(β) = M. Следовательно, следствие 2 непосредственно вытекает изтеоремы 5, примененной к отрезку [α; β], если α β, или, соответственно, к отрезку [β; α], если β < α.Таким образом, множество всех значений функции, заданной и непрерывной на некотором отрезке, представляетсобой также отрезок.