
- •1.Понятия множества. Логические символы.
- •2.Операции над множествами. Отображение множеств.
- •5.Лемма о вложенных отрезках.
- •6. Лемма о конечном покрытии.
- •7. Лемма о предельной точке числового множества.
- •8. Предел числовой последовательности и общие свойства предела.
- •9.Предел.Переход. И арифмет. Операц.
- •11. Критерий Коши существования предела числовой последоват.
- •12. Существование предела монотонной огран. Послед.
- •13.Подпоследовательность. Теорема Больцано-Вейерштрасса о выделении сходящейсяподпоследовательности
- •14.Предел функции. Эквивалентность опр.По Коши и по Гейне
- •15. Общие свойства предела функции и арифметические операции.
- •16.Предел ф-ции и неравенства.
- •17. Односторонние пределы.
- •18.Предел.Отнош. Синуса. К. Аргумент.
- •19 .Число е.
- •21. Непрерывность ф-ции в точке.
- •22.Точки разрыва функции.
- •23. Предел композиции (сложной функции). Непрерывность композиции функций.
- •24.Огранниченность ф-циинепрер. На отрезке.
- •25. Промежуточные значения непрерывных функций.
- •26. Непрерывность обратной функции на отрезке.
- •27. Непрерывность обратной функции на интервале.
- •28. Равномерная непрерывность функций.
- •29. Непрерывность элементарных функций.
- •30. Дифференцируемость функций. Дифференциал и производная.
- •31. Непрерывность функции, имеющей производную.
- •32. Геометрический смысл производной и дифференциала. Физический смысл производной.
- •33. Правила вычисления производных
- •34. Дифференцирование композиции функций.
- •35. Производная обратной функции.
- •36. Производные элементарных функций.
- •37. Производные и дифференциалы высших порядков. Формула Лейбница.
- •1. Производные высших порядков.
- •2.Дифференциалы высших порядков.
- •38. Теорема Ферма.
- •39. Теорема Ролля.
- •40. Теорема Лагранжа.
- •41. Теорема Коши.
- •42. Раскрытие неопределенностей вида
- •43. Раскрытие неопределенностей вида
- •44. Формула Тейлора.
- •45. Разложения основных элементарных функций по формуле Тейлора.
- •46. Условие монотонности функции.
- •47. Экстремум функции.
- •48.Выпуклость функции
- •49. Tочки перегиба
- •50. Некоторые классические неравенства.
- •1.Неравенства Юнга.
- •2. Неравенство Гельдера.
- •3. Неравенство Минковского.
- •51. Неопределенный интеграли его основные свойства.
- •52. Интегрирование подстановкой в неопределенном интеграле.
- •53. Интегрирование по частям в неопределенном интеграле.
- •54. Разложение правильной рациональной дроби в сумму простейших.
- •55. Интегрирование простейших рациональных дробей.
- •56. Интегрирование некоторых тригонометрических функций.
- •57.Интегрирование некоторых иррациональных функций.
- •58.Интегрирование биноминального дифференциала
- •59. Понятие определенного интеграла. Необходимое условие существования интеграла Римана.
- •60. Критерий Коши интегрируемости функций.
- •61. Достаточное условие интегрируемости функции.
- •62.Классы интегрируемых функций.
- •64. Критерий Дарбу интегрир. Ф-ций.
- •65. Линейность, монотонность, аддитивность и общая оценка определенного интеграла.
- •3. Аддитивность интегралов.
- •4. Монотонность интеграла.
- •66.Теорема о среднем для интеграла.
- •67.Интеграл с переменным верхним пределом, его свойства.
- •68. Формула Ньютона-Лейбница.
- •69. Замена переменной в определенном интеграле.
- •70. Интегрирование по частям. Остаточный член формулы Тейлора в интегральной форме.
- •71. Некоторые приложения определённого интеграла.
17. Односторонние пределы.
Определение
5. Число y0
называется левосторонним пределом
функции y =
f(x)
в точке x0,
если для любого ε
>0существует
δ >0,
такое, что
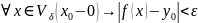 и
обознается
и
обознается
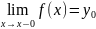 .
.
Определение 6. Число y0 называется правосторонним пределом функции y = f(x) в точке x0, если для любого ε> 0
существует
δ>
0, такое, что ∀x∈Vδ(x0
+ 0) ⇒
|f(x)
− y0|
<ε
и обозначается
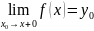 .
.
Теорема 12. Чтобы функция f(x) в точке x0 имела предел, необходимо и достаточно, чтобы она имела оба одно-
сторонних предела равных между собой. Тогда общее значение этих односторонних пределов равно пределу функции
f(x) в точке x0.
Док-во:Необходимость. Пусть.
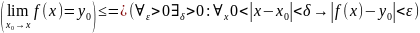
Но тогда имеем, что будет справедливо и
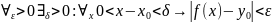 и
и
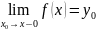 .
Аналогично
.
Достаточность. Пусть
.
Аналогично
.
Достаточность. Пусть
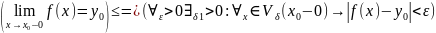 и
и
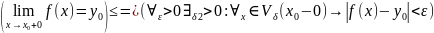
Обозначимδ=min{δ1,δ2}.
Тогда из –δ<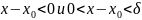 следует,
что 0<
следует,
что 0< .т.е
.т.е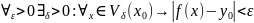 или
или
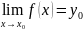 .
.
18.Предел.Отнош. Синуса. К. Аргумент.
Докажем,
что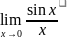 Так
как f(x) =
Так
как f(x) =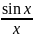 является четной функцией, то рассмотрим
ее только на интервале (0;
является четной функцией, то рассмотрим
ее только на интервале (0;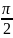 )Возьмем дугу AM единичного круга,
соответствующую углу, радианная мера
которого равна x. Площадь сектораOAM
заключена между площадями треугольников
OMA и OTA:S
)Возьмем дугу AM единичного круга,
соответствующую углу, радианная мера
которого равна x. Площадь сектораOAM
заключена между площадями треугольников
OMA и OTA:S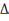 OMA
<Sсек< S4OAT ⇔
OMA
<Sсек< S4OAT ⇔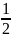 ·
|OA| · |PM| <
·
|OA|2·
x <
·
|OA| · |AT|. Так как |OA| = 1, |MP| = sin x, |AT| = tg x, то
sinx<x<tgx⇔
1 <
·
|OA| · |PM| <
·
|OA|2·
x <
·
|OA| · |AT|. Так как |OA| = 1, |MP| = sin x, |AT| = tg x, то
sinx<x<tgx⇔
1 <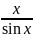 ·<
·<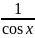 ⇔cosx<
<
1. В силу четности функции cosx
и
последнее двойное неравенство справедливо
и для интервала ( -
; 0). Таким образом, для любого x ∈(
-
; 0)∪(0;
)выполняется неравенство cosx<
<
1Переходя к пределу при
⇔cosx<
<
1. В силу четности функции cosx
и
последнее двойное неравенство справедливо
и для интервала ( -
; 0). Таким образом, для любого x ∈(
-
; 0)∪(0;
)выполняется неравенство cosx<
<
1Переходя к пределу при
x
→ 0 получим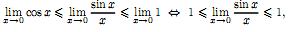
т.е. =1 – который называют первым замечательным пределом.
19 .Число е.
Пример 1. Доказать справедливость неравенства (неравенство Я. Бернулли)
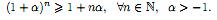
Решение. Докажем, основываясь на методе математической индукции.
1. При n = 1 утверждение, очевидно, справедливо.2. Предположим, что оно справедливо при n = k, т.е. верно (1 + α)k> 1 + kα.
3.
Докажем, что оно справедливо при n =
k+1.Действительно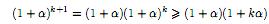
![]()
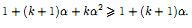 Согласно
методу математической индукции заключаем,
что утверждение справедливо ∀n
∈
N.Рассмотрим последовательность {xn},
где
Согласно
методу математической индукции заключаем,
что утверждение справедливо ∀n
∈
N.Рассмотрим последовательность {xn},
где
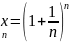 Покажем,
что последовательность {yn},
где
Покажем,
что последовательность {yn},
где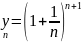 убывающая.
Действительно ∀n
2, находим
убывающая.
Действительно ∀n
2, находим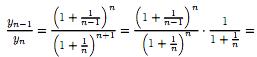
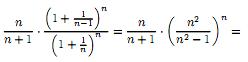
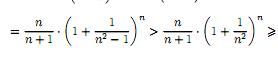
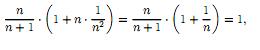
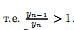 Очевидно,
что все члены последова-тельности {yn}
имеют положительные члены, а следова-тельно,
согласно теоремеВейерштрасса, она имеет
предел. Тогда
Очевидно,
что все члены последова-тельности {yn}
имеют положительные члены, а следова-тельно,
согласно теоремеВейерштрасса, она имеет
предел. Тогда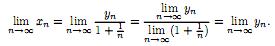
Определение
1.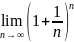 =е
=е
20. Бесконечно малые и большие функции. Символы ~, о, О. Сравнение функций
Определение
1. Функция
f(x) называется бесконечно малой функцией
(или бесконечно малой) при x → x0
если
=0
Определение
2. Функция
f(x) называется бесконечно большой
функцией (или бесконечно большой) при
x → x0
если
=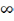 Теорема
13.Если функция
f(x) при x → x0
– бесконечно большая, то функция
Теорема
13.Если функция
f(x) при x → x0
– бесконечно большая, то функция
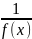 при x → x0
– бесконечно малая. Если функция f(x)
при x
→ x0
– бесконечно малая, то функция
при
x
→ x0
– бесконечно большая. ]
при x → x0
– бесконечно малая. Если функция f(x)
при x
→ x0
– бесконечно малая, то функция
при
x
→ x0
– бесконечно большая. ]
Свойства бесконечно малых функций.
Т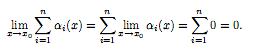 еорема
14. Конечная
сумма бесконечно малых функций при x
→ x0,
есть функция, бесконечно малая при x
→ x0.
Доказательство.
Если αi(x),
i
= 1, n
– бесконечно малые функции при x
→ x0,
то
еорема
14. Конечная
сумма бесконечно малых функций при x
→ x0,
есть функция, бесконечно малая при x
→ x0.
Доказательство.
Если αi(x),
i
= 1, n
– бесконечно малые функции при x
→ x0,
то
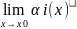 =0
,i
= 1, n
=0
,i
= 1, n
Теорема
15. Произведение
бесконечно малой функции при x → x0
и функции, ограниченной в
(x0),
есть бесконечно малая функция при x →
x0.
Следствие1.
Произведением
некоторого числа и бесконечно малой
функции при x → x0
есть бесконечно малаяфункция при x →
x0.Теорема
16. Частное
от деления бесконечно малой функции
α(x) при x → x0
на
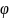 (x),
такую, что
(x),
такую, что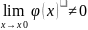 есть
бесконечно малая функция при x → x0.
есть
бесконечно малая функция при x → x0.
Д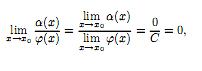 оказательство.
Так как α(x) – бесконечно малая функция,
то
оказательство.
Так как α(x) – бесконечно малая функция,
то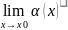 =0Тогда
=0Тогда
где
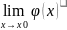 = C
0.
= C
0.
