12. Существование предела монотонной огран. Послед.

Определение 2.Последовательность {x_n} называется возрастающей (строго возрастающей) если x_n+1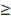 x_n (x_n+1>x_n) для ∀n ∈ N.Последовательность {x_n} называется убывающей (строго убывающей) если x_n+1 x_n (x_n+1<x_n) для ∀n ∈ N.Определение 3. Возрастающие и убывающие последо-вательности называются монотоннымипоследователь-ностями.Теорема 5 (Вейерштрасс). Для того чтобы неубывающая последовательность имела предел, необходимо и доста-точно, чтобы она была ограниченной сверху. Доказательство. То, что любая сходящаяся последова-тельность ограничена, было доказано при рассмотрении общихсвойств предела последовательности.Пусть {x_n} неубывающая последовательность ограниченная сверху. Тогда множество {x_n | n ∈ N} ограничено сверху.Согласно основной лемме это множество имеет верхнюю грань a = supx_n. По определению верхней грани для любогоε > 0 найдется элемент x_N∈ {x_n} такой, что a−ε <x_N a. Поскольку последовательность {x_n} неубывающая, то прилюбом n > N получаем a − ε <x_N x_n a, т.е. a − ε <x_n<a+ε или |x_n−a| < ε.

Поэтому _n=a.

13.Подпоследовательность. Теорема Больцано-Вейерштрасса о выделении сходящейсяподпоследовательности

Теорема 6. (Больцано-Вейерштрасса). Из всякой ограниченной последовательности можно извлечь сходящуюсяподпоследовательность.Доказательство. Пусть X – множество значений ограниченной последовательности {x_n}. Если X конечное множество,то тогда очевидно найдется a∈ X который будет повторяться в последовательности бесконечное число раз.Пусть онповторяется под номерами n₁< n₂< . . . <n_k< . . .Тогда последовательность {x_nk} постоянна т.к. x_nk = a, ∀k ∈ изначит сходится.

Если X бесконечно, то согласно лемме 5 оно обладает по крайней мере одной предельной точкой a. Поскольку a –предельная точка множества X то можно выбрать n₁∈ так, что |x_n1 − a| <1. Если n_k∈ уже выбрано так, что|x_nk−a| <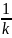 , то учитывая, что a предельная точка множества X, найдем n_k+1 ∈ так, что n_k< n_k+1 и |x_nk+1−a| < .

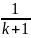Поскольку 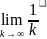=0, то построеннаяподпоследовательностьx_n1 , x_n2 , . . . , x_nk , . . . сходится к a.

Замечание 1. Мы имеем, что всякая сходящаяся подпоследовательность ограничена, обратное вообще говоря неверно,например, x_n = (−1)ⁿ. Однако для ограниченной последовательности имеет место указанная выше теорема.

14.Предел функции. Эквивалентность опр.По Коши и по Гейне

Пусть функция f(x) определена в проколотой окрестности точки x0 т.е. на множестве V_δ(x0)= {x : 0 < |x−x0| < δ}. В точке x0 значение f(x0) может быть не определено.

Определение 1 (по Коши, или, на языке «ε − δ» ). Число y0 называется пределом функции y = f(x) в точке x0 (или, при x → x0), если для любого ε > 0 можно указать такое число δ = δ(ε) > 0, что при всех x, удовлетворяющих условию 0 < |x − x0| < δ, выполняется неравенство |f(x) − y0| < ε, или:

y₀=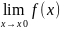 ⇔∀ε > 0 ∃δ> 0:∀x 0 < |x − x0| < δ ⇒|f(x) − y0| < ε . В определении 1 используются понятия ε-окрестности и проколотой δ-окрестности. Если обозначить

Vε(y0) = {y = f(x) : |f(x) − y0| <ε}, V_δ(x0) = {x : 0 < |x − x0| <δ}, тоегократкозаписываютещеввиде y₀=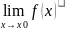 ⇔∀ε> 0 ∃δ> 0 ∀x ∈V_δ(x0) ⇒ f(x) ∈ Vε(y0). Определение 2 (по Гейне, или, на языке последо-вательностей). Число y₀ называется пределом функции y = f(x) в точке x0 (или, при x → x0), если для любой последовательности точек xn∈V_δ(x₀), сходящейся к x0, последовательность соответствующих значений функции f(x_n) сходится к

y₀: y₀= ⇔∀xn : n=x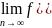0⇒ n) = y0 .

Докажем эквивалентность определений(1)и(2).

Пусть 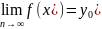по коши. Расмотрим{x_n} такую, что x_n → x₀ при n → ∞. Так как x_n → x₀ при n → ∞. То 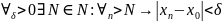, а поэтому и .

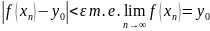Пусть y₀есть предел функцииf(x) при x→ x₀ по Гейне, т.е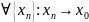 при n → ∞. Следует, что f(x_n)→y₀при n → ∞.

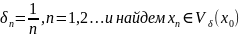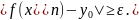Пусть y₀ не есть предел функции f(x) при x → x₀ по Коши. Возьмем , где при этом будем иметь Значит имеем {x_n}такую, что x_n → x₀ при n → ∞. И кроме того , что противоречит оределение по Гейне.