
- •1.Понятия множества. Логические символы.
- •2.Операции над множествами. Отображение множеств.
- •5.Лемма о вложенных отрезках.
- •6. Лемма о конечном покрытии.
- •7. Лемма о предельной точке числового множества.
- •8. Предел числовой последовательности и общие свойства предела.
- •9.Предел.Переход. И арифмет. Операц.
- •11. Критерий Коши существования предела числовой последоват.
- •12. Существование предела монотонной огран. Послед.
- •13.Подпоследовательность. Теорема Больцано-Вейерштрасса о выделении сходящейсяподпоследовательности
- •14.Предел функции. Эквивалентность опр.По Коши и по Гейне
- •15. Общие свойства предела функции и арифметические операции.
- •16.Предел ф-ции и неравенства.
- •17. Односторонние пределы.
- •18.Предел.Отнош. Синуса. К. Аргумент.
- •19 .Число е.
- •21. Непрерывность ф-ции в точке.
- •22.Точки разрыва функции.
- •23. Предел композиции (сложной функции). Непрерывность композиции функций.
- •24.Огранниченность ф-циинепрер. На отрезке.
- •25. Промежуточные значения непрерывных функций.
- •26. Непрерывность обратной функции на отрезке.
- •27. Непрерывность обратной функции на интервале.
- •28. Равномерная непрерывность функций.
- •29. Непрерывность элементарных функций.
- •30. Дифференцируемость функций. Дифференциал и производная.
- •31. Непрерывность функции, имеющей производную.
- •32. Геометрический смысл производной и дифференциала. Физический смысл производной.
- •33. Правила вычисления производных
- •34. Дифференцирование композиции функций.
- •35. Производная обратной функции.
- •36. Производные элементарных функций.
- •37. Производные и дифференциалы высших порядков. Формула Лейбница.
- •1. Производные высших порядков.
- •2.Дифференциалы высших порядков.
- •38. Теорема Ферма.
- •39. Теорема Ролля.
- •40. Теорема Лагранжа.
- •41. Теорема Коши.
- •42. Раскрытие неопределенностей вида
- •43. Раскрытие неопределенностей вида
- •44. Формула Тейлора.
- •45. Разложения основных элементарных функций по формуле Тейлора.
- •46. Условие монотонности функции.
- •47. Экстремум функции.
- •48.Выпуклость функции
- •49. Tочки перегиба
- •50. Некоторые классические неравенства.
- •1.Неравенства Юнга.
- •2. Неравенство Гельдера.
- •3. Неравенство Минковского.
- •51. Неопределенный интеграли его основные свойства.
- •52. Интегрирование подстановкой в неопределенном интеграле.
- •53. Интегрирование по частям в неопределенном интеграле.
- •54. Разложение правильной рациональной дроби в сумму простейших.
- •55. Интегрирование простейших рациональных дробей.
- •56. Интегрирование некоторых тригонометрических функций.
- •57.Интегрирование некоторых иррациональных функций.
- •58.Интегрирование биноминального дифференциала
- •59. Понятие определенного интеграла. Необходимое условие существования интеграла Римана.
- •60. Критерий Коши интегрируемости функций.
- •61. Достаточное условие интегрируемости функции.
- •62.Классы интегрируемых функций.
- •64. Критерий Дарбу интегрир. Ф-ций.
- •65. Линейность, монотонность, аддитивность и общая оценка определенного интеграла.
- •3. Аддитивность интегралов.
- •4. Монотонность интеграла.
- •66.Теорема о среднем для интеграла.
- •67.Интеграл с переменным верхним пределом, его свойства.
- •68. Формула Ньютона-Лейбница.
- •69. Замена переменной в определенном интеграле.
- •70. Интегрирование по частям. Остаточный член формулы Тейлора в интегральной форме.
- •71. Некоторые приложения определённого интеграла.
8. Предел числовой последовательности и общие свойства предела.
Опр.2 Число a наз. Пределом числовой последовательности {xn}, если для любого сколь угодно
малого положительного числа ε найдется такое натуральное число n0 = n0 (ε), что для всех n>n0 выполняется
неравенство |xn-a|< ε
В этом случае говорят, что последовательность имеет предел и пишут limn→∞xn= a.
Теорема 1.
а) Финально постоянная последовательность сходится;
б) Если последовательность имеет предел, то он единственный;
в) Сходящаяся последовательность ограничена.
Доказательство.
А)Если xn =Aпри n>n0ϵN, то для любой окрестности V(A) точки А имеем xn ϵV(A) при n>n0, т.е. limn→∞xn= А.
Б)
Пусть limn→∞xn=
a.иlimn→∞xn=
b,
при чем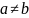 тогда по опр. Предела последовательности
имеем
тогда по опр. Предела последовательности
имеем

И
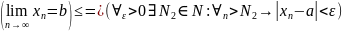
Положим N = max{N1,N2}. Тогда ∀ε >0 ∀n > N будет справедливо |xn–a|< ε и |xn− b| < ε. Откуда
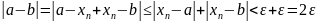
т.е. 1/2|a − b| < ε для ∀ε >0. Последнее возможно только при a = b.
В) пусть limn→∞xn= a.тогда по опред. Предела
Т.е.
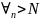 будет
выполнятсяa-ε<xn<a+ε,
aтем
более
будет
выполнятсяa-ε<xn<a+ε,
aтем
более
–(|a|+ε)<xn<(|a|+ε)
ПустьМ=max{|x1|,|x2|,…,|xn|,|a|+ε}.
Тогда получим, что |xn|≤M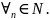
9.Предел.Переход. И арифмет. Операц.
Арифмет. Операц. Определение 3. Если {xn}, {yn} - две числовые последовательности,то их суммой,произведением и частным называются соответственно последовательности {xn + yn}, {xnyn}, {xn/yn} (при делении предполагается, что все членыпоследовательности {yn} отличны то нуля).
Теорема
2. Если последовательности {xn},
{yn}
сходятся и n=aи
n=aи
 n=bто,
а)
n
n=bто,
а)
n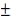 yn=
n
yn=
n n=a
n=a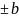 б)
б)
 n=c
n=c*a,
c
n=c
n=c*a,
c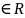 \{0}
в)
nyn=
n
n=a*b
г)
\{0}
в)
nyn=
n
n=a*b
г)
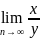 =
n\
n=a\b
=
n\
n=a\b
Доказательство. Докажем случай г). Имеем. n=a
⇔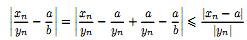
![]() ∀ε>
0 ∃N1∈N
:∀n>N1⇒
|xn
− a|
<εи
n=b⇔∀ε>
0 ∃N2∈N
: ∀n>N2
⇒
|yn
− b|
<ε . Посколькуb
∀ε>
0 ∃N1∈N
:∀n>N1⇒
|xn
− a|
<εи
n=b⇔∀ε>
0 ∃N2∈N
: ∀n>N2
⇒
|yn
− b|
<ε . Посколькуb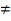 0, то∃δ>
0 ∃N3∈N
: ∀n>N3⇒
|yn|
>δ> 0. Пусть N = max{N1,N2,N3}.
Тогда имеем
0, то∃δ>
0 ∃N3∈N
: ∀n>N3⇒
|yn|
>δ> 0. Пусть N = max{N1,N2,N3}.
Тогда имеем
![]()
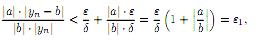
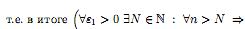
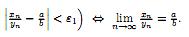
Если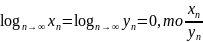 называют
неопределенностью вида
называют
неопределенностью вида
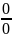 .
. Для вычисления
такого предела теорема 2неприменима.
Вычисление пределов для неопределенных
выражений вида
.
. Для вычисления
такого предела теорема 2неприменима.
Вычисление пределов для неопределенных
выражений вида
 1∞,
∞−∞,
0·∞ называют
раскрытиемсоответствующих неопределенностей.
1∞,
∞−∞,
0·∞ называют
раскрытиемсоответствующих неопределенностей.
10.
Предельный переход и неравенства
Если
 и
в некоторой проколотой окрестности
точки a
справедливо неравенство f(x)≤g(x),
то b≤c.
и
в некоторой проколотой окрестности
точки a
справедливо неравенство f(x)≤g(x),
то b≤c.
Д-во:
Допустим
противное b>c.
Тогда
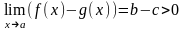 и по теореме о сохранении знака в
некоторой проколотой окрестности
и по теореме о сохранении знака в
некоторой проколотой окрестности
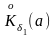 справедливо
неравенство f(x)-g(x)>0.
По условию в некоторой проклотой
окрестности
справедливо
неравенство f(x)-g(x)>0.
По условию в некоторой проклотой
окрестности
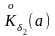 справедливо
неравенство f(x)≤
g(x).
Пусть
справедливо
неравенство f(x)≤
g(x).
Пусть
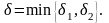 .
Тогда в
.
Тогда в
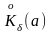 должны
быть справедливы оба неравенства, f(x)≤
g(x)
и f(x)>g(x),
что невозможно.
должны
быть справедливы оба неравенства, f(x)≤
g(x)
и f(x)>g(x),
что невозможно.
Предельный переход в равенстве.
Пусть
существует окрестность такая, что для
всех точек X
верно f(x)=g(x),
и при этом существует

11. Критерий Коши существования предела числовой последоват.
Определение 1. Последовательность {xn} называется фундаментальной (или последовательностью Коши), если для любого числа ε > 0 найдется такой номер N ∈ N, что из n > N и m > N следует |xn − xm| < ε.
Теорема 4 (критерий Коши сходимости последовательности). Числовая последовательность сходится тогда и только тогда, когда она фундаментальна.
Док-во.Необходимость.
Пусть
n=aТогда,
согласноопределения, ε>
0 ∃N∈ : ∀l>N⇒
|xl
− a|
<
: ∀l>N⇒
|xl
− a|
< Еслитеперьm>Nиn>N,
то |xm
− xn|
= |xm
− a
+ a
− xn|
Еслитеперьm>Nиn>N,
то |xm
− xn|
= |xm
− a
+ a
− xn|
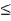 |xm
− a|
+ |xn
− a|
<
+
=
|xm
− a|
+ |xn
− a|
<
+
= т.е.
сходящаясяпоследовательностьфундаментальна.
т.е.
сходящаясяпоследовательностьфундаментальна.
