4. Монотонность интеграла.
Теорема
12
(одна общая оценка интеграла). Если
a
6
b
и
f
∈R[a;
b],
то |f|
∈R[a;
b]
и
справедливо неравенство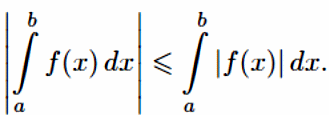
Если
при этом f(x)
6 C
на
[a;
b],
то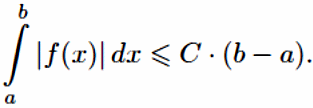
Доказательство. При a = b утверждение тривиально, поэтому будем считать, что a < b.Для доказательства теоремы прежде всего следует убедиться, что |f(x)| интегрируема, если f(x) интегрируема.Последнее легко следует из очевидного условия
Далее
дадим оценку интегральной суммы
Переходя
к пределу при |τ
|
→ 0,
получаем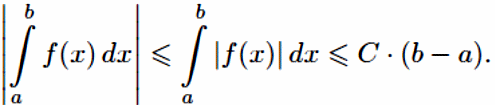
Теорема
13
(монотонность интеграла). Если
a
≤b,
f1,
f2
∈R[a;
b]
и
f1(x)
≤f2(x)
в
любой точке x
∈[a;
b],
то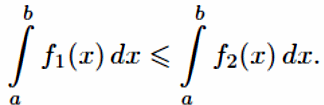
Доказательство.При
a
=
b
утверждение
тривиально. Если же a
< b,
то достаточно записать для интегральных
суммнеравенство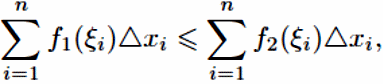
справедливое,
поскольку △
>0,
i
=
1до
n,
и затем перейти в нем к пределу при |τ
|
→ 0.
66.Теорема о среднем для интеграла.
Теорема 15 (Первая теорема о среднем для интеграла). Пусть f, g ∈ R[a; b], m =
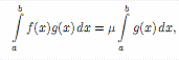Если
функция g(x) неотрицательна (или не
положительна) на отрезке [a; b], то
(1)
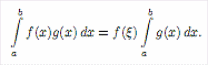где
µ ∈
[m;M]. Если, кроме того, известно, что f ∈
C[a; b], то найдется ξ ∈
[a; b] такая, что
(2)
Доказательство.
Поскольку перестановка пределов
интегрирования приводит к изменению
знака одновременно в обеих частях
равенства (1), то достаточно проверить
это равенство в случае a < b. Изменение
знака функции g(x) тоже одновременно
меняет знак обеих частей равенства (1),
поэтому без ограничения общности
доказательства будем считать, что g(x)
0 на [a; b].
Поскольку
то при g(x)
0 имеем
Поскольку
m · g ∈
R[a; b], f · g ∈
R[a; b], M · g ∈
R[a; b], то, применяя теорему 13, получим
Е
сли
то, как видно из этих неравенств,
с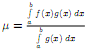
оотношение
(1) выполнено. Если же
то
полагая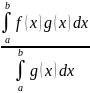
находим, что µ ∈ [m;M], но это равносильно соотношению (1). Равенство (2) следует из (1) из теоремы о промежуточном значении для функции f ∈ C[a; b], с учетом того, что в случае
f ∈ C[a;b]
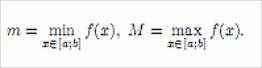
67.Интеграл с переменным верхним пределом, его свойства.
Пусть f ∈ R[a; b]. Тогда согласно лемме 1 она интегрируема на любом отрезке [a; x] ⊂ [a; b]. Рассмотрим функцию
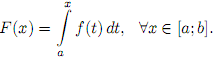
Эта функция называется интегралом с переменным верхним пределом.
Теорема
17. Если
f∈R[a;b],
то при любом x∈[a;b]
определена функция
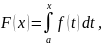(3.20)
и F(x) ∈
C[a; b].
Доказательство. Существование интеграла (3.20) при любом x ∈ [a; b] следует из леммы 1, поэтому остается проверить
непрерывность функции F(x). Поскольку f∈C[a;b], то|f(x)|≤M<∞ на [a; b]. Пусть x ∈ [a; b] и x+h∈ [a; b]. Тогда в силу аддитивности интеграла получаем
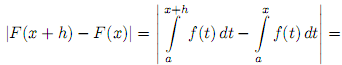
Отсюда следует, что limh→0|4F(x)| = 0, а это и означает, что функция (3.20) непрерывна в каждой точке x∈ [a; b].
Теорема 18. Если f∈R[a; b] и функция f(x) непрерывна в некоторой точке x∈ [a; b], то функция F(x), определенная
на [a; b] формулой (3.20), дифференцируема в этой точке x, причем имеет место равенство F’(x) = f(x).
Доказательство. Пусть x∈ [a; b], x + h∈ [a; b]. Оценим
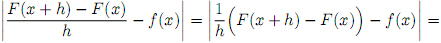
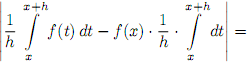
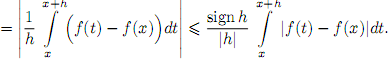
Так как f(x) непрерывна в точке x, то
∀ε>0 ∃δ>0: ∀t∈[a;b] |t−x|<δ⇒|f(t)−f(x)|<ε.
Пусть |h| < δ. Тогда
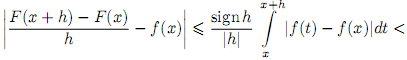
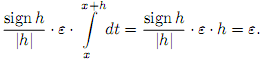
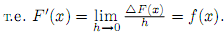
Отметим, что если x = a или x = b, то под F(x) понимаем соответствующие односторонние производные.
Теорема 19. Каждая непрерывная на отрезке [a; b] функция f(x) имеет на этом отрезке первообразную, причем
любая первообразная функции f(x) на [a; b] имеет вид
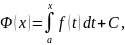(3.21)
где C - некоторая постоянная.
Доказательство. Поскольку f∈C[a; b], то f∈R[a; b], поэтому, на основании теоремы 18, функция (3.20) является
первообразной для f(x) на [a; b]. Но две первообразные Φ(x) и F(x) одной и той же функции на отрезке могут отличаться
на этом отрезке только на постоянную, поэтому Φ(x) = F(x) + C.