64. Критерий Дарбу интегрир. Ф-ций.
Теорема 9 (Критерий Дарбу). Для того, чтобы ограниченная на отрезке функция была на нем интегрируема по
Риману, необходимо и достаточно, чтобы были равны ее верхний и нижний интегралы Дарбу.
Доказательство.
Необходимость. Пусть функция f(x) интегрируема на [a; b]. Так как sτ<= I∗<= I∗<= Sτ , то 0 <= I∗ − I∗<= Sτ − sτ , и
так
как для интегрируемой функции
то I∗ = I∗
Достаточность. Если f(x) ограничена на отрезке [a; b] функция и I∗ = I∗, то, в силу теорем 7 и8
что и означает интегрируемость функции f(x) на отрезке [a; b].
65. Линейность, монотонность, аддитивность и общая оценка определенного интеграла.
Прежде всего заметим, что интеграл от функции является числом, сопоставляемый заданной функции согласноданному ранее определению, поэтому это число не зависит от выбора обозначения для аргумента подынтегральнойфункции, то есть от обозначения переменной интегрирования.
1.
.
Действительно,
здесь подынтегральная функция равна
единице, поэтому при любом разбиенииτ
=
все интегральные суммы Римана
равны
b
−
a:
2. Линейность интегралов.
Теорема 10. Если f(x) и g(x) интегрируемые на отрезке [a; b] функции, то их линейная комбинация αf(x) + βg(x)
также является интегрируемой на отрезке [a; b] функцией, причем
2.11
Доказательство.
Каковы
бы ни были разбиения τ
=
отрезка
[a;
b]
с диаметром |τ
|
и
точки ξi
∈[
;
],
i
=
1 до
nимеет
место равенство
где
(αf
+βg),
(f),
(g)
- интегральные суммы функции αf(x)+βg(x),
f(x),
g(x)
соответственно. Так как функцииf(x),
g(x)
интегрируемы на [a;
b],
то существуют пределы
,
,а
тогда и
А это и означает, что функция αf(x) + βg(x) интегрируема на [a; b] и имеет место равенство (2.11).
Равенство (2.11) выражает линейность интегралов.
3. Аддитивность интегралов.
Лемма 1. Если функция f(x) интегрируема на отрезке [a; b], то она интегрируема на любом отрезке [c; d], содержа-
щемся в отрезке [a; b].
Доказательство. Прежде всего, если функция f(x) ограничена на отрезке [a; b], то она, очевидно, ограничена и наотрезке [c; d].
Далее,
каково бы ни было разбиение τ’=
отрезка
[c;
d]
⊂[a;
b]
диаметра |τ
′|,
его всегда можно продолжить вразбиениеτ
=
отрезка [a;
b]
такого же диаметра: для этого достаточно
добавить к точкам
,
i
=
1 до
n′
конечноечисло
соответствующим образом выбранных
точек принадлежащих отрезку [a;
b],
но не принадлежащих отрезку [c;
d].
Полагая
и
замечая, что каждое слагаемое суммы
является
и слагаемым суммы
и
что все
слагаемые
обеих сумм неотрицательны, имеем
Если
функция f(x)
интегрируема на отрезке [a;
b],
то,
.
Но поскольку |τ
|
=
|τ
′|,
то из предыдущегонеравенства следует,
что
Отсюда и следует интегрируемость f(x) на [c; d].
Теорема
11.Если
a
< b < c и
f
∈R[a;
c](функция
f(x)
интегрируема
по Риману на отрезке [a;
c]),
то
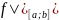∈R[a;
b],
∈R[b;
c],и
имеет место равенство
Доказательство.
Если
τ1
- разбиение отрезка [a;
b]
с диаметром |τ1|,
τ2
- разбиение отрезка [b;
c]
с диаметром |τ2|,
то τ
=
τ1
∪τ2
явл. разбиением отрезка [a;
c]
с диаметром |τ
|
=
max {|τ1|,
|τ2|}.
Тогда для интегральных сумм функцииf(x)
и ее сужений
,
выполнено
равенство
+
=
Так как f(x) интегрируема на [a; c], то согласно лемме 1, , интегрируемы на [a; b] и [b; c] соответственно.Переходя в (2.13) к пределу при |τ | → 0 получим равенство (2.12).
Равенство (2.12) выражает аддитивность интегралов.
Из
теоремы 11 непосредственно следует