57.Интегрирование некоторых иррациональных функций.

Они вычисляются подстановкой x = t^s, где s - общий знаменатель дробей m1/n1,m2/n2, . . . При такой замене переменной интеграл приводится к рациональной функции от переменной t.

Эти интегралы подстановкой ax+b/cx+d = t^s, где s - общий знаменатель дробей m1/n1,m2/n2, . . ., сводятся к рациональной функции от переменной t.

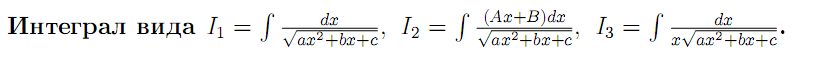
Пусть для определённости a> 0.

Для вычисления интеграла I1 применяется подстановка x+(b/2a) = u. В результате этот интеграл сводится к табличному du/(u²±k²)^0.5 Действительно

Для вычисления I2 преобразовываем подынтегральную функцию

Вычисление интеграла I₃ сводится к вычислению интеграла I₁ подстановкой x = 1/u .

Частные случаи вычисления интегралов данного вида рассмотрены в предыдущих пунктах. Существует несколько

различных приёмов их вычисления. Рассмотрим один из таких приёмов, основанный на применении тригонометрических подстановок.Квадратный трёхчлен ax²+bx+c путём выделения полного квадрата и замены переменной может быть представлен

в виде u² ± k². Таким образом, достаточно ограничиться рассмотрением трёх видов интегралов

58.Интегрирование биноминального дифференциала

Рассматриваемые интегралы, называемые интегралами от дифференциального бинома x^m(a+bxⁿ)^pdx выражаются

через элементарные функции только в следующих трех случаях:

1 . Если p ∈ Z, то применяется подстановка x = t^s , где s - общий знаменатель дробей m и n;

2 . Если( m+1) /n∈Z, то применяется подстановка a + bxⁿ = t^s, где s - знаменатель дроби p = k/s ;

3⁰. Если (m+1/n) + p∈Z, то применяется подстановка ax⁻ⁿ + b = t^s, где s - знаменатель дроби p.

59. Понятие определенного интеграла. Необходимое условие существования интеграла Римана.

Теорема 1. Если функция f(x) интегрируема на отрезке [a; b], то она ограничена на этом отрезке.

Доказательство. Пусть функция f(x) не ограничена на отрезке [a; b] и пусть фиксировано некоторое разбиениеτ = {x_i}i=ni=0 этого отрезка. В силу неограниченности функции f(x) на всем отрезке [a; b], она не ограничена по крайней мере на одном отрезке разбиения τ . Пусть для определенности функция f(x) не ограничена на отрезке [x₀; x₁]. Тогда

на этом отрезке существует последовательность ξ₁^(m)∈ [x₀; x₁], m = 1, 2, . . ., такая, что

Зафиксируем теперь каким-либо образом точки ξi∈ [x_i−1; x_i], i = 2, n. Тогда сумма

будет иметь определенное значение. Потому, в силу (1.2)

и, следовательно, каково бы ни было число M> 0, всегда можно подобрать такой номер m0, что если на первом отрезке[x₀; x₁] взять точку ξ₁^(m0) , то

Отсюда следует, что суммы στ не могут стремится ни к какому конечному пределу при |τ | → 0. Полученное противоречие доказывает теорему Условия ограниченности функции f(x), будучи необходимыми для ее интегрируемости, не являются вместе с тем достаточными. Действительно, рассмотрим функцию Дирихле

Рассмотрим эту функцию на отрезке [0;1]. Она, очевидно, ограничена на нем. Покажем, что она не интегрируем по Риману. Зафиксируем произвольные разбиения τ = {x_i}i=ni=0 отрезка [0; 1]. Если выбрать точки ξ_i∈ [x_i−1; x_i], i = 1, рациональными, то получим

а если взять ξiиррациональными, то

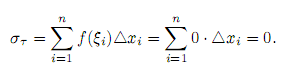
Так как это для любого разбиения τ , то интегральные суммы στ заведомо не стремятся к пределу при |τ | → 0.