49. Tочки перегиба

Определение 3. Точка x₀ называется точкой перегиба функции f(x), если при переходе через точку x₀ функцияменяет характер выпуклости.

Теорема 20 (необходимое условие точки перегиба). Если функция f(x) имеет непрерывную в точке x₀ производную f’’(x) и x₀ – точка перегиба, то f’’(x₀) = 0.

Доказательство. Если бы в точке перегиба x0 выполнялось неравенство f’’(x₀) > 0 или f’’(x₀) < 0, то в силу непрерывности f’’(x) существовала бы окрестность точки x0, в которой f’’(x) > 0 или f’’(x) < 0. По теореме 19 в этой окрестности функция была бы выпукла вниз или вверх соответственно, что противоречит наличию перегиба в точке x₀.

Из теоремы 20 следует, что точками возможного перегиба функции f(x) могут быть точки x0 в которых f’’(x₀) = 0, либо точки, в которых f’’(x) не существует, в частности она бесконечна.

Теорема 21 (первое достаточное условие перегиба). Если функция f(x) дважды непрерывно дифференцируема вокрестности точки x₀ и при переходе через точку x₀ производная f’’(x) меняет знак, то точка x₀ является точкойперегиба функции f(x).

Доказательство. Пусть, к примеру, f’’(x) > 0 при x<x₀ и f’’(x)<0 при x>x₀. Тогда по теореме 19 функция f(x) выпукла вниз на интервале (x; x₀) и выпукла вверх на интервале (x₀; x), т.е. x₀ – точка перегиба.

Теорема 22 (общее достаточное условие перегиба). Пусть в точке x₀ для функции f(x) выполнены условия f’’(x₀)=f’’’(x₀)=...=f⁽ⁿ⁻¹⁾ (x₀)=0

и в точке x₀ существует непрерывная производная f (x₀), n> 2, причём f (x₀) = 0. Если n – нечётное число, тов точке x₀ функция f(x) имеет перегиб.

Доказательство. Разлагая f(x) по формуле Тейлора n−1-го порядка с учетом условия получаем

f(x) = f(x₀) + f’(x₀)(x − x₀) + 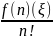(x − x₀)ⁿ, (5.32)

где ξ расположена между x₀ и x.

Если Y (x) = f(x₀) + f’(x₀)(x − x₀) уравнение касательной к графику функции f(x) в точке (x₀, f(x₀)), то из (5.32) имеем

f(x) − Y (x) = (x − x₀)ⁿ, (5.33) где n – нечётное.

В силу непрерывности f⁽ⁿ⁾(x) в точке x₀ существует окрестность этой точки, в которой производная f⁽ⁿ⁾(x) сохраняет знак, совпадающий со знаком f⁽ⁿ⁾(x₀). Поэтому можем считать, что знаки f⁽ⁿ⁾(x₀) и f⁽ⁿ⁾(ξ) совпадают. Тогда из равенства (5.33) получаем, что при переходе x через x₀ слева направо график функции располагается по разные стороны от касательной, т.е. в точке (x₀, f(x₀)) имеется перегиб.

50. Некоторые классические неравенства.

1.Неравенства Юнга.

Если a >0, b >0, а числа p, q таковы, что p ≠ 0; 1, q ≠ 0; 1 и 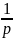+ 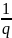= 1, то (6.38; 6.39)

причем знак неравенства в (6.38), (6.39) имеет место только при a = b.

Доказательство.Достаточно в (6.36) и(6.37) положить x = 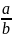и α = , а также ввести обозначение .

2. Неравенство Гельдера.

Пусть Тогда (6.40)

и 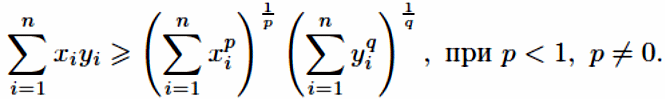(6.41)

В случае p <0 в (6.41) предполагается, что xi >0, i = 1, n.Знак равенства в (6.40) и (6.41) возможен только в случае пропорциональности векторов ( ), ( ).

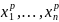Доказательство. Проверим неравенство (6.40). Пусть

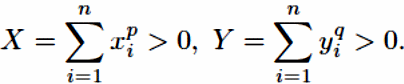
Полагая в (6.38) a = 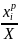,b= 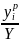, получаем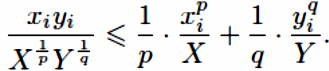

Суммируя эти неравенства по i от 1 до n, получаем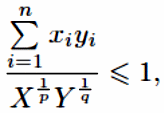 это эквивалентно (6.40).

Аналогично из (6.39) получаем (6.41). Поскольку знак равенства в (6.38) и (6.39) возможен лишь при a = b, заключаем, что в (6.40) и (6.41) он возможен лишь при пропорциональност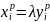и или .