45. Разложения основных элементарных функций по формуле Тейлора.
Разложение
основных элементарных функций
- Положив
и
вычислив соответствующие производные
в нуле, получим формулы Тейлора для
основных элементарных функций:
;
;
;
;
;
;
.
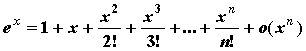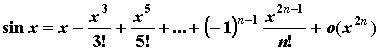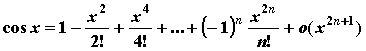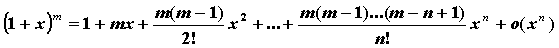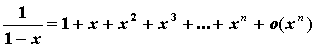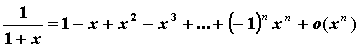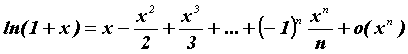46. Условие монотонности функции.
Теорема13.
Для того чтобы дифференцируемая
наинтервале (a; b) функция f(x) возрастала
(убывала) необходимои достаточно, чтобы
во всех его точках производная была
неотрицательной, т. е. f’(x)
0 (неположительной,f’(x)
0).Доказательство.Необходимость.
Если функция f(x) возрастает на (a; b), то
для любой точки x0 ∈
(a; b) при
x
> 0 имеем
y
= f(x0
+
x)
− f(x0)
0. Поэтому
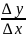0 и переходя к пределу при
x
→ 0, получим f
’(x)
0.
Достаточность.
Пусть a < x1<
x2<
b. Тогда, по формуле Лагранжа f(x2)
− f(x1)
= f’(ξ)(x2
− x1),
где x1<
x2.
Так как x2
− x1>
0, то при f’(x)
0 на (a;
b)
(откуда следует, что, в частности, f’(ξ)
0) будем иметь f(x1)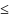
f(x2)
т. е. функция f(x)
возрастает.
Следствие 1. Если функция непрерывна на некотором интервале и имеет всюду в нём положительную (отрицательную) производную, кроме, быть может, конечного числа точек, в которых производная обращается в нуль или не существует, то функция строго возрастает (строго убывает).
Доказательство непосредственно следует из теоремы 13: достаточно её последовательно применить ко всем промежуткам, на которые разбивается заданный интервал указанным конечным множеством точек.
47. Экстремум функции.
Теорема 14. Пусть x0 является точкой экстремума функции f(x), определённой в некоторой окрестности точки x0. Тогда либо производная f’(x0) не существует, либо f’(x0) = 0.
Доказательство. Действительно, если x0 является точкой экстремума для функции f(x), то найдётся такая окрестность V (x0), что значение функции f(x) в точке x0 будет наибольшим, или наименьшим на этой окрестности. Поэтому если в точке x0 существует производная, то она, согласно теореме Ферма равна нулю.
Геометрический смысл теоремы 14 заключается в следующем: в точках экстремума функции f(x) касательная к её графику параллельна оси абсцисс, если существует f’(x0) = 0; параллельна оси ординат, если f’(x0) бесконечна; существуют не совпадающие левая и правая касательные, если f’(x0 − 0) f’(x0 + 0).Точки, в которых функция y = f(x) определена, а ее производная равна нулю, или не существует, называют критическими. Точки, в которых функция y = f(x) определена, а ее производная равна нулю, называют стационарными.
Теорема 15 (Первый достаточный признак существования экстремума функции). Пусть x0 - критическая точка непрерывной функции f(x). Если f’(x) при переходе через точку x0 меняет знак с «+» на «-», то x0 - точка локального максимума; если f’(x) при переходе через точку x0 меняет знак с «-» на«+», то x0 - точка локального минимума; если f’(x) при переходе через точку x0 не меняет знак, то x0 не является точкой локального экстремума.
Теорема 16 (Второй достаточный признак существования экстремума функции). Стационарная точка x0 функции f(x), дважды дифференцируемой в V (x0), является точкой локального минимума если f’’(x0) > 0, и точкой локального максимума, если f’’(x0) < 0.
Теорема 17 (Третий достаточный признак существования экстремума функции).Пусть функция f(x) n раз непрерывно дифференцируема в точке x0 и f’(x0) = f’’(x0) = . . . = f(n−1)(x0) = 0,f(n)(x0) 0. Тогда:
1) если n - чётное и f(n)(x0) < 0, то x0 - точка локального максимума;
2) если n - чётное и f(n)(x0) > 0, то x0 - точка локального минимума;
3) если n - нечётное, то x0 - не является точкой локального экстремума.