42. Раскрытие неопределенностей вида

Остановимся на одном частном, но полезном приеме отыскания предела отношения функций, известном как правилоЛопиталя.

Теорема 10 (Неопределенность вида 0/0 ).Пусть:

1) функции f(x) и g(x) определены в промежутке (a; b];

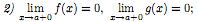
3) в промежутке (a; b] существуют конечные производные f’(x) и g’(x), причем g’(x) 0; 4) существует (конечный или бесконечный) предел

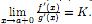
Доказательство. Дополним определения функций f(x) и g(x), положив их при x = a равными нулю: f(a) = g(a) = 0. Тогда эти функции окажутся непрерывными во всем замкнутом промежутке [a; b]; их значения в точке a совпадают спределами при x → a, а в прочих точках непрерывность вытекает из существования конечных производных. Применяятеорему Коши, получим

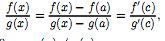
где a < c < x. То обстоятельство, что g(x) 0, т.е. g(x) g(a) есть следствие предложения g’(x) = 0. Когда x → a, очевидно, и c → a, так что, в силу условия 4)

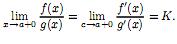
43. Раскрытие неопределенностей вида

Теорема 11 (Неопределенность вида ∞/∞).

Пусть: 1) функции f(x) и g(x) определены в промежутке (a; b];

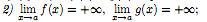
3) существуют в промежутке (a; b] конечные производные f’(x) и g’(x), причем g’(x) 0;

4) существует (конечный или бесконечный) предел

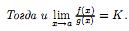
Доказательство. Рассмотрим сначала случай конечногоK.

Так как производная g′(x) не обращается в нуль, то она сохраняет знак, и функция g(x) изменяется монотонно. Из условия 2) тогда ясно, что g′(x) <0 так как g(x) с убыванием x монотонно возрастая стремится к +∞. Можно считать, что всегда g(x) >0.

Взяв произвольным образом число ε >0, в силу условия 4), найдем такое η >0, что при a < x < a + η будет .

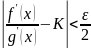Положим для краткости a + η = x0 и возьмем x между a и x0. К отрезку [x; x0] применим формулу Коши 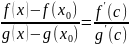, где x<c<x0 и следовательно, . Поскольку

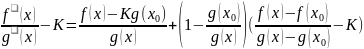
То | .

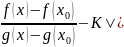Второе слагаемое справа для x < x0 = a + η будет меньше ε/2, в силу (4.12). Ввиду того же, что g(x) → +∞ при x → a, первое слагаемое при этом стремится к нулю, и найдется такое δ >0 (можно считать δ < η), что для a < x <a+δпервое слагаемое тоже станет меньше ε/2. Для указанных значений x будем иметь тогда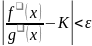 , что доказывает требуемое утверждение.

44. Формула Тейлора.

Имеем, что дифференцируемую функцию f(x) в окрестности точки x₀ можно представить в виде f(x) = f(x₀) + f’(x₀)(x − x₀) + o(x − x₀), x → x₀,т.е. существует многочлен первой степени P₁(x)=f(x₀)+A·(x−x₀), такой, что при x → x0 имеет место равенство f(x) = P₁(x) + o(x − x₀), причем многочлен P₁(x) удовлетворяет условиям P₁(x0) = f(x₀), P’₁(x₀) = f’(x₀). Поставим более общую задачу.

Пусть функция f(x) определена в некоторой окрестности точки x₀ и имеет в этой точке n производных f’(x₀), f’’(x₀), . . . , f⁽ⁿ⁾(x₀). Найдем многочлен P_n(x) степени не выше n, такой, что

f(x) = P_n(x) + o((x − x₀)ⁿ), x → x0, (1),

Будем искать многочлен P_n(x) в виде

P_n(x) = A₀ + A₁(x − x₀) + A₂(x − x₀)²+ . . . + A_n(x − x₀)ⁿ

Отсюда, дифференцируя, последовательно находим:

P’_n(x) = A₁ + 2A₂(x − x₀) + 3A₃(x−x₀)²+ . . . +nA_n(x − x₀)ⁿ⁻¹. P’’_n(x) = 2·1* A₂+3·2* A₃(x − x₀)+4·3·A₄(x − x₀)²+...+ n(n−1)A_n(x−x₀)ⁿ⁻²,

P⁽ⁿ⁾_n (x) = n(n − 1)(n − 2) · . . . · 3 · 2 · 1 · A_n.

Tеперьполучаем :

f(x₀)=P_n(x⁰)=A₀⇒A₀=f(x₀);f’(x₀)=P’_n(x₀) = A₁⇒A₁ = f’(x₀);

Теорема 12. Пусть функция f(x) определена в некоторой окрестности точки x₀ и n раз дифференцируема в ней. Тогда при x→x₀ имеет место формула

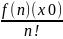f(x)=f(x₀)+f’(x₀)(x−x₀)+ (x−x₀)²+...+ (x − x₀)ⁿ+ o((x − x₀)ⁿ) ,

эта называется формулой Тейлора n-го порядка с остаточным членом в форме Пеано, где R_n(x) =f(x)−P_n(x)=o((x − x0)ⁿ), x→x0 – остаточный член.