34. Дифференцирование композиции функций.

Теорема 4.Еслифункция f : X → Y ⊂ R дифференцируемавточке x, афункцияg : Y → R дифференцируемавточке y = f(x) ∈ Y , токомпозиция g ◦ f : X → R этихфункцийдифференцируемавточке x, причем (g ◦ f)’(x) = g’(f)*f ’(x).

Доказательство. Условиядифференцируемостифункций f и g имеютвид f(x + h) − f(x) = f ‘(x)h + o(h), h → 0, x + h ∈ X, g(y + t) − g(y) = g’(y)t + o(t), t → 0, y + t ∈ Y.

Заметим, что в силу последнего равенства функцию o(t) можно считать определенной и при t = 0, а в представлении o(t) = γ(t) · t, где γ(t) → 0 при t → 0, y + t∈Y , можно считать γ(0) = 0. Полагая f(x) = y, f(x + h) = y + t в силу дифференцируемости, а значит, и непрерывности функции f в точке x заключаем, что при h → 0 также t → 0, и если x + h∈X, то y + t∈Y . По теореме о пределе композиции теперь имеем

γ (f(x + h) − f(x)) = α(h) → 0, h → 0, x + h∈X и, таким образом, т.к. t = f(x + h) − f(x), то

o(t)=γ(f(x+h)−f(x))(f(x+h)−f(x))=α(h)(f’(x)h+o(h))=α(h)f’(x)h+α(h)o(h)=o(h)+o(h)=o(h), h → 0, x + h∈X.

Далее

(g◦f)(x+h)−(g◦f)(x)=g(f(x+h))−g(f(x))=g(y+t)−g(y)=g‘(y)t+o(t)=g‘(y)(f(x+h)−f(x))+o(f(x+h)−f(x))=g’(y)(f’(x)h + o(h))+o(f(x + h) − f(x))= g’(y)f ’(x)h + g’(y)o(h) + o(f(x+h) − f(x)).

Заметим, чтосуммаg’(y)o(h) + o(f(x + h) − f(x)) естьвеличинабесконечномалаявсравнениисhприh → 0,x + h∈Xт.к.

o(f(x + h) − f(x))= o(h), h → 0, x + h∈X.

Витоге (g ◦ f)(x + h) − (g ◦ f)(x) = g’(f) · f’(x)h + o(h), h → 0, x + h∈X.

35. Производная обратной функции.

Теорема 5 (О производной обратной функции). Пусть функции f: X→Y, f^-1: Y→X взаимно обратны и непрерывны в точках x₀∈X и f(x₀) = y₀∈Y соответственно. Если функция f(x) дифференцируема в точке x₀ и f≠0, то функция f^-1 также дифференцируема в точке y₀ , причем (f^-1)’(y₀)=1/f’(x₀).

Доказательство.Из непрерывности f(x) в x₀ и f^-1в y₀ можно заключить, что при x→x₀ , x∈X имеем y = f(x) → y₀, y=f(x) ∈ Y и y=f(x)≠ y₀ , если x≠x₀ . Используя теперь теорему о пределе композиции функций и арифметические свойства предела, находим .

Таким образом, показано, что в точке y₀ функция f⁻¹: Y→X имеет производную и (f^-1)’(y₀)=1/f’(x₀).

Замечание 1. Если бы заранее было известно, что функция f⁻¹ дифференцируема в точке y₀, то из тождества (f⁻¹○f)(x) ≡ x по теореме о дифференцировании композиции функции сразу бы нашли, что (f⁻¹)’ (y₀ )·f’(x₀) = 1.

Замечание 2. Теореме можно дать геометрическую интерпретацию. Как известно,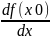 =tgα, где α – значение угла, образуемого касательной графика функции f(x) в точке (x₀, y₀ ) с положительным направлением оси Ox, тогда

, где β – значение угла, образованного той же касательной с осью Oy.

Действительно, поскольку β = −α, то

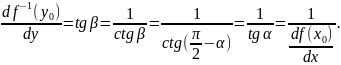
36. Производные элементарных функций.

а). Производная и дифференциал логарифмической функции. Пусть y = log _a x, где a > 0,a 1. Тогда

y = log a (x + x) – log _a x = log _a(1 +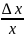 ). Следовательно, по определению

y₀= = =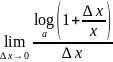 log_a = log_ae= .Здесь воспользовались вторым замечательным пределом и непрерывностью логарифмической функции. Итак, y = log_ax⇒y₀= log_ae= ⇒dy = .

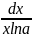б). Производная и дифференциал степенной функции Пусть y =(u(x))^α, α∈R. Рассмотрим вначале случай, когда u(x) > 0. Если u(x) > 0, то lny = αlnu(x). Продифференцируем полученное равенство почленно по правилу дифференцирования сложной функции, считая y функцией от x: (lny)’ = (αlnu(x))’ ⇒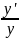 = 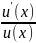⇒dy = .

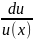Пусть теперь u(x) < 0. Представим функцию y = (u(x))^α в виде (−1)^α (v(x))^α , где v(x) > 0. Тогда

y’= (−1)^αα(v(x))^α−1v’(x) = α(u(x))^α−1u’(x).

Итакy =(u(x))^α⇒y’= α(u(x))^α−1u’(x) ⇒dy = α(u(x))^α−1du(x).