32. Геометрический смысл производной и дифференциала. Физический смысл производной.

Рассмотрим задачу о проведении касательной кпроизвольной плоской кривой. Пусть L – дуга плоской кривой, M₀ –точка этой кривой, M₀M – секущая. Если точка M движется по кривой к точке M₀,то секущая поворачивается вокругточки M₀ и стремится к некоторому предельному положению M₀T.Определение 4. Касательной к кривой L в точке M₀ называется прямая M₀T, которая представляет собой предельноеположение секущей M₀M при стремлении по кривой точки M к точке M₀.Если предельного положения секущей не существует, то говорят, что в точке M₀ провести касательную нельзя. Этобывает в случае, когда точка M₀ является точкой излома или заострения кривой.Пусть кривая L является графиком функции f(x) и точка M₀(x₀, f(x₀)) ∈ L. Предположим, что касательная ккривой в точке M₀ существует. Угловой коэффициент секущей M₀Mk = tg = . Если x → 0, то точка M движется по кривой к точке M₀ и секущая M₀M стремится к своему предельному положению M₀T. Таким образом, k = tgα = = =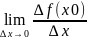f ’(x0). (1) т.е. если кривая L является графиком функции f(x), то из равенства (1) следует геометрический смысл производной: производная от функции f(x) при x = x₀ равна угловому коэффициенту касательной к графику функции в точке с абсциссой x .Тогда уравнение касательной y − f(x0) = f’(x0)(x − x0)или y − y0 = f ’(x0)(x − x0) (2).Заметим, что в правой части уравнения (2) стоит дифференциал, поэтому геометрический смысл дифференциала состоит в следующем: дифференциал - это приращение ординаты касательной.физика:Рассмотрим функцию y = f(x), определенную и непрерывную в некоторой окрестности точки x0. Если аргумент x0функции получает приращение

x (положительное или отрицательное), такое, что x0+ x принадлежит той же окрестности точки x0, то соответствующее приращение функции f(x0) = f(x0 + x) − f(x0), средняя скорость измененияфункции v_ср = , а мгновенная скорость ее измененияv = =f ’(x0)В этом состоит механический смысл производной, т.е.производная -математическая модель мгновенной скоростипроцесса, описываемого функцией f(x). В зависимости от содержательной сущности функции можно получить широкийкруг математических моделей скорости протекания процессов. Рассмотрим некоторые из них.1. Пусть материальная точка M движется неравномерно и y = s(t) – функция, устанавливающая зависимость путиот времени t. Тогда мгновенная скорость движения в момент времени t₀ есть производная от пути s по времени t:

v =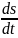 |_t=t0= =

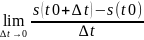
33. Правила вычисления производных

Теорема 3. Если функции f : X → R, g : X → Rдифференцируемы в точке x ∈ X, то

а) их сумма дифференцируема в x, причем(f+g)’(x)=(f’+g’)(x);

б) их произведение дифференцируемо в x, причем (f · g)’(x) = f’(x)g(x) + f(x)g’(x);

в) их отношение дифференцируемо в x, если g(x) 0, причем( 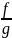)‘(x) =

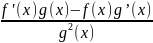
Следствие 1. Производная от линейной комбинации дифференцируемых функций равна линейной комбинации производных этих функций.

Следствие 2. Если функции f₁(x), f₂(x), . . . , f_n(x) дифференцируемы в точке x, то. (f₁ · f₂ · . . . · f_n)’(x) = f’₁(x) · f₂(x) · . . . · f_n(x) + f₁(x) · f’₂(x) · . . . · f_n(x) + . . . + f₁(x) · f₂(x) · . . . · f’_n(x).

Следствие 3.Из взаимосвязи производной и дифференциала следует, что теорема 3 может быть записана такжечерез дифференциалы, т.е.

а) d(f + g)(x) = df(x) + dg(x),

в) d(f · g)(x) = g(x) · df(x) + f(x) · dg(x);

с) d( )(x) =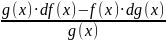 , если g(x) 0.