30. Дифференцируемость функций. Дифференциал и производная.

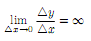О пределение 1. Пусть функция y = f(x) определена в некоторой окрестности точки x0 ∈ R и пусть x–произвольнаяточка этой окрестности. Если отношение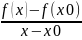 имеет gредел при x → x0, то этот предел называется производной функции f(x) в точке x₀, и обозначается f ’(x₀): 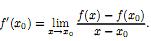Если ввести обозначения x−x₀ = x, f(x₀+ x)−f(x₀) = y, то получаем еще одну запись определения производной: Если для

н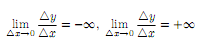 екоторого значения x₀ существуют пределы или то говорят, что при x = x₀

существует бесконечная производная или соответственно бесконечная производная определенного знака, равная − или + .В дальнейшем под выражением «функция имеет производную» будем понимать всегда наличие конечной производной, если не оговорено противное.

О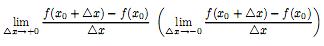 пределение 2. Если функция f(x) определена в некоторой правосторонней (левосторонней) окрестности точки x₀ исуществует конечный или бесконечный (определенного знака) предел

то он называется соответственно конечной или бесконечной правой (левой) производной функции f(x) в точке x₀ иобозначается f ’₊(x₀) (f ’₋(x0)) Правая и левая производные называются односторонними производными. Из теоремы об односторонних пределах следует, что функция f(x), определенная в некоторой окрестности точки x₀,имеет производную f ’(x₀) тогда и только тогда, когда f ’₊(x0) и f ‘₋(x₀) существуют и f’₊(x0) = f’₋(x0). В этом случае f’(x0) = f’₊(x0) = f’₋(x0).Если функция f(x) определена на некотором промежутке и в каждой его точке существует производная (причем под производной в конце этого промежутка, который принадлежит промежутку, понимается соответствующая односторонняя производная), то она также является функцией, определенной на данном промежутке, ее обозначают f’(x).

Теорема 1. Для того чтобы функция f(x) была дифференцируемой в некоторой точке x0, необходимо и достаточно,чтобы она имела в этой точке производную, при этом dy = f’(x0) dx.Доказательство. Пусть функция f(x) дифференцируема в точке x0, т.е y = A· x+o( x), x → 0.Тогда 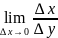= A + 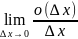= A.Поэтому производная f’(x0) существует и равна A. Отсюда dy= f’(x0) dx.

Теорема 2. Если функция f(x) дифференцируема в некоторой точке, то она и непрерывна в этой точке. Следствие 1. Если функция в некоторой точке имеет производную, то она и непрерывна в этой точке.Обратим внимание на то, если функция в точке имеет бесконечную производную, то она может быть разрывной в этой точке. Заметим, что утверждение, обратное теореме 2, неверно, т.е. из непрерывности функции f(x) в данной точке не следует ее дифференцируемость.

31. Непрерывность функции, имеющей производную.

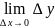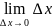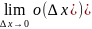Теорема 2. Если функция f(x) дифференцируема в некоторой точке, то она и непрерывна в этой точке.Доказательство. Пусть функция f(x) дифференцируема в точке x₀, т.е y = A · x + o( x), x → 0. = A + = 0,что и означает непрерывность функции f(x) в точке x₀.

Следствие 1. Если функция в некоторой точке имеет производную, то она и непрерывна в этой точке.Обратим внимание на то, если функция в точке имеет бесконечную производную, то она может быть разрывной в этой точке. Заметим, что утверждение, обратное теореме 2, неверно, т.е. из непрерывности функции f(x) в данной точке не следует ее дифференцируемость.