28. Равномерная непрерывность функций.

О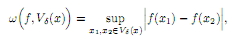 пределение 1. Функция f(x) называется равномерно-непрерывной на множестве X ⊂ R, если для любого ε > 0найдется δ = δ(ε) > 0, такое, что для любых x₁, x₂∈ X, удовлетворяющих условию |x₁−x₂| < δ, выполняется неравенство|f(x₁) − f(x₂)| < ε.

Если f(x) равномерно-непрерывна на множестве X, то она непрерывна на множестве X. Чтобы в этом убедиться,достаточно положить x₁ = x, x₂ = x₀. Тогда из определения равномерной непрерывности функции следует определениенепрерывной функции в точке x₀. Обратное утверждение не всегда справедливо.

Теорема 8 (Кантора). Функция, непрерывная на отрезке, равномерно непрерывна на этом отрезке.Доказательство. Пусть f : X → R, и f ∈ C([a; b]), где X = [a; b]. Поскольку f(x) непрерывна в любой точке x ∈ X, топо ε > 0 можно найти такую δ-окрестность V_δ(x) точки x, что колебание ω(f, V_δ(x)), где

функции f(x) окажется меньше ε.Для каждой точки x ∈ X построим окрестность V_δ(x) обладающую этим свойством. Величина δ при этом может меняться от точки к точке, т.е. δ = δ(x). Интервалы V_δ/2(x), x ∈ X в совокупности образуют покрытие отрезкаX = [a; b], из которого по лемме о конечном покрытии можно выделить конечное подпокрытиеV_δ/2(x1), . . . , V_δ/2(xn).

Пустьδ = min{ δ(x₁), . . . , δ(x_n)}. Покажем, что для любых точек x’, x’’∈ X таких, что |x’− x’’| < δ выполнено|f(x’) − f(x’’)| < ε. Действительно, поскольку система интервалов V_δ/2(x₁), . . . , V_δ/2(x_n) покрывает X, то найдется интервал V_δ/2(x_i) этой системы, который содержит точку x’ т.е. |x’− x_i| < δ(x_i). Но в таком случае |x’’− x_i| |x’− x’’| + |x’− x_i| <δ + δ(x_i) < δ(x_i) + δ(x_i) = δ(x_i). Следовательно x’, x’’∈V_δ(xi)(x_i) и потому |f(x’) − f(x’’)| ω(f, V_δ(xi)(x_i))< ε.

29. Непрерывность элементарных функций.

П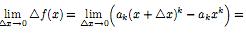 остоянная функция.Функция f(x) = C, где C = const, ∀x ∈ X непрерывна в любой точке x0, поскольку = =С=f(x₀). Многочлены и рациональные функции.ФункцияP_n(x) = a₀xⁿ + a₁xⁿ⁻¹+ . . . + aⁿ⁻¹x + aⁿ,где a_i, i = 0, n – действительные числа, называется многочленом от x степени n.Докажем сначала непрерывность функции f(x) = a_kx^k в любой точке x ∈ R. Согласно биному Ньютона

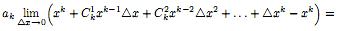
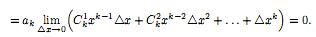
О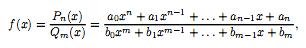 тсюда заключаем, что функция f(x) = a_kx^k непрерывна в любой точке x∈R. Тогда многочлен P_n(x) является непрерывной функцией в любой точке x∈R как сумма непрерывных функций вида a_kx^k, k = 0, n. Рациональной называется функция вида

г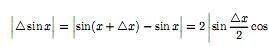 де P_n(x), Q_m(x) – многочлены степеней n и m cоответственно. Рациональная функция во всех точках, в которых Q_m(x) не обращается в нуль, непрерывна как отношениедвухнепрерывных функций.

Тригонометрические функции:Докажем непрерывность функции f(x) = sin x в любой точке x ∈ R. Имеем

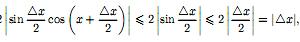
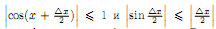
так как Отсюда следует, что если | x| < δ = ε, то и | sin x| < ε, т.е. sin xнепрерывная функция в любой точке x ∈ R.Аналогично доказывается непрерывность функции cos x в любой точке x ∈ R.Функция tg x = непрерывна в точках, где x + πn, n ∈ Z. Функция ctg x = непрерывна, если x πn,n ∈ Z.

Степенная функция f(x) = x^a. Непрерывность этой функции при x> 0 вытекает из непрерывности сложной функции и представления x^a = e^alnx. Если же функция x^a имеет смысл и для x < 0 (например, x⁴,³√x), то при a > 0 она будет непрерывной для ∀x ∈ R, апри a < 0 – для всех x ∈ R кроме x 0.