32.I замечательный предел.

ТЕОР1: Предел функции g(x) = в точке х = 0 существует и равен 1, т.е. lim =1

n

Док-во: Рассмотрим дугу окружности радиуса R=1 с центральным углом, радиальная мера которого равна Х (0<X</2).

Т огда АО=1, sin X=MK, tg X=AT.

Площадь треугольника ОАМ меньше площади сектора ОАМ, которая меньше площади треугольника ОАТ, или 1/2ОАМК<1/2OAAM<1/2OAAT  1/2sin X<1/2X<1/2tg X  sin X<X<tg X. Разделим эти неравенства на sin X>0, получим 1< < . Для обратных величин справедливы обратные неравенства cosX< <1.

Так как неравенства справедливы при 0<X</2  они справедливы и при -/2<X<0, так как при замене Х на –Х все три функции cosX, (sin X)/X и 1 не меняют своих значений. Т. о. неравенства справедливы при всех Х(-/2, /2), за исключением точки Х=0.

Так как обе функции f(x)=cosX и h(x)=1 имеют в точке Х=0 предел равный 1, то g(x)= тоже имеет в точке Х=0 предел равный 1.

32.II замечательный предел.

ТЕОР1: Предел функции f(x) = при х существует и равен числу е, т.е. lim = e.

х

Док-во: Пусть X>1.

Положим n=[x] (целая часть Х), тогда X=n+, где n – натуральное число, а  удовлетворяет условию 0<1. Так как nX<n+1, 1/(n+1)<1/X1/n и 1+1/(n+1)<1+1/X1+1/n, то (по свойству возрастания показательной Ф. с основанием, большим 1) < < 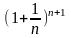. При Х (n) lim =lim lim =e1=e и lim =[lim ]/[lim ]=e.  lim =e.

Пусть теперь X<-1, X= -Y.

Тогда lim =lim =lim =lim lim = e1=e

(при X -, Y +).

Окончательно имеем lim = e.

33.Бесконечно малые функции. Действия над ними.

ОПР1: Функция называется бесконечно малой в точке х=А (или при хА), если предел этой функции в точке А равен 0.

ОПР2: (К) Функция (х) называется бесконечно малой в точке х=А (или при хА), если для любого положительного числа  >0 существует >0 такое, что для всех хХ, удовлетворяющих условию 0<|x – A|<, выполняется неравенство |(x)|<.

(>0)(=()>0)(xX,0<|x – A|<):|(x)|<

ОПР3: (Г) Функция (х) называется бесконечно малой в точке х=А (или при хА), если для любой сходящейся к А последовательности {Xn} значений аргумента Х, отличных от А, соответствующая последовательность значений функции {(Xn)} является бесконечно малой. ({Xn}A, XnA):{F(Xn)} – б-м

ТЕОР1: Для выполнения равенства limf(x)=b необходимо и достаточно, чтобы функция

х

(х)=f(х) - b была бесконечно малой при хa.

Док-во: Необходимость: пусть limf(x)=b. Рассмотрим разность (х)=f(х) – b и докажем, что (х) – бесконечно малая функция при хa. Действительно lim (х)=lim(f(х) – b)=limf(x) – lim b=b – b=0.

Достаточность: Пусть (х)=f(х) – b, где (х) – бесконечно малая функция при хa. Докажем, что limf(x)=b. Так как f(x)=b+(х), то limf(x)= lim(b+(х))= lim b+ lim (х) =b+0=b.

ТЕОР2: Алгебраическая сумма и произведение конечного числа бесконечно малых функций при ха, а также произведение бесконечно малой функции на ограниченную являются бесконечно малыми функциями при ха.

Док-во: Вытекает из определения предела функции по Гейне и свойств бесконечно малых последовательностей.