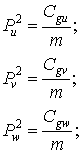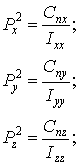- •1 Внешние воздействующие факторы. Классификация.
- •Механические и внешние воздействующие факторы:
- •Климатические ввф.
- •2 Внешние воздействующие факторы космической среды.
- •4. Особенности проекторования системы виброизоляции при однонаправленной схеме нагружения
- •5. Конструктивные особенности системы виброизоляции
- •Система с 2-мя плоскостями симметрии.
- •Система с одной плоскость симметрии.
- •Система без плоскостей симметрии
- •6.Виды диссипативных сил, действующих в системе виброизоляции. Их разновидности и реализация в виброизоляторе. Основные виды диссипативных сил.
- •7.Вынужденные колебания системы виброизоляции при пассивной виброизоляции Пассивная виброизоляция.
- •8 Основные виды воздействующих факторов на рэа . Механичекие воздействия их основные виды и применения.
- •9.11. Энергетические соотношения в системе виброизоляцииции. Уравнение Лагранжа
- •10. Характеристики виброизоляторов, используемых при расчёте системы на ударные воздействия и их применение
- •12. Статический и динамический расчет Статический расчет системы
- •Динамический расчет
- •14 Определение инерционных параметров.
- •15 Неравенство Релея
- •16 Определение собственных частот системы виброизоляции через парциальные частоты
- •17 Электрическое моделирование системы виброизоляции
- •18. Статический расчет системы. Определение координат центра тяжести объекта.
- •19 Частотная зависимость коэффициента динамичности системы виброизоляции.
- •20 Основные этапы инженерной методики вибрационного расчета системы виброизоляции блока рэс.
- •Определение коэффициента динамичности при наличии диапазонов собственных и воздействующих частот
- •21 Жесткостные параметры системы виброизоляции. Статическая и динамическая жесткость системы виброизоляции
- •Методика расчета системы амортизации при вибрационных воздействиях
- •1. Статический расчет системы.
- •Динамический расчет системы амортизации.
- •Статический расчет системы
- •Установка амортизаторов, выбор типоразмера амортизатора
- •Выбор типоразмера амортизатора.
- •Выравнивание блока в положение равновесия
- •Для трех амортизаторов
- •Динамический расчет
- •22 Жесткостные и инерционные параметры систем виброизоляции
- •Свободное движение объекта вязким трением с одной степенью свободы.
- •25. Свободное движение блока на виброизоляторах, использующих силы сухого трения.
- •26. Колебания блока рэс с шестью степенями свободы. Особенности определения собственных частот системы виброизоляции.
- •27. Рекомендации по проектированию системы виброизоляции
- •28. Виды и классификация сил в системе виброизоляции
- •Основные виды диссипативных сил
- •Возмущающие силы
- •29. Определение собственных частот системы виброизоляции при трех, двух и одной плоскости симметрии
- •Система с 2-мя плоскостями симметрии
- •Система с одной плоскость симметрии
- •30. Парциальные частоты системы и их определение через параметры системы
- •32. Методики расчёта на ударные воздействия (упрощённая и метод эквивалентных прямоугольных импульсов).
- •31. Основные виды виброизоляторов и их характеристики.Нормализованные и ненормализованные виброизоляторы
- •1. Амортизатор демпфированный (ад).
- •4. Плоскостные или чашечные амортизаторы ап (ач)
- •33. Метод эквивалентных прямоугольных импульсов при расчёте системы виброизоляции на ударные воздействия
- •Методика расчета.
- •34. Свободное движение блока на виброизоляторах
- •Свободное движение объекта с одной степенью свободы в системе с вязким трением:
- •Малое затухание системы
- •35. Коэффициент динамичности. Его роль при расчёте системы виброизоляции. Эффективность виброизоляции
- •36 (Вместе с 35). Частотная зависимость коэффициента динамичности
- •Определение коэффициента динамичности при наличии диапазонов собственных и воздействующих частот
- •Эффективность амортизации.
- •Тепло- и массобмен в эвс. Защита эвс от тепловых воздействий.
- •1 Пути обеспечения температурной стабильности и теплостойкости эвс.
- •Тепло.Вопрос№2 Конструктивные способы уменьшения теплового контактного сопротивления
- •3, Дифференциальное уравнение теплопроводности.
- •Тепло.Вопрос№4 Сравнение штыревых и ребристых радиаторов.
- •5. Метод электротепловой аналогии.
- •Аналогии.
- •Выражение для rtc.
- •Неустановившийся режим для плоской стенки.
- •Тепло.Вопрос№6 охлаждение транзисторов.
- •7. Передача тепла конвекцией.
- •Виды и режимы движения хладогентов.
- •Тепло.Вопрос№8 (Возможно это не то что надо ,но это всё что хоть как то связано с этим вопросом )
- •9. Уравнение энергии (Бернулли).
- •10. Критерий Рейнольдса.
- •11. Гидравлические характеристики рэс и нагнетателя.
- •Принцип суперпозиции.
- •Характеристики нагнетателя.
- •Определение рабочей точки и выбор нагнетателя.
- •12 Повышение эффективности теплообмена путем оребрения поверхности.
- •13. Понятие о теории подобия и критериях подобия.
- •14. Естественная конвекция.
- •15. Передача тепла излучением.
- •16 Сложный теплообмен. Закон ньютона-римана.
- •17. Простейшая методика подбора теплоотвода для охлаждения полупроводниковых приборов (ост 4 го.010.030):
- •18 Уравнение теплопродности стационарный и не стационарный тепловые режимы
- •19 Передача тепла теплопроводностью. Температурный градиент. Закон Фурье.
- •20 Уравнение теплопроводности. Коэффициент температуропроводности. Дифференциальное уравнение теплопроводности
- •21 Одномерное установившееся поле плоской стенки, составных тел. Одномерное установившееся поле плоской стенки.
- •Одномерное установившееся поле составных тел. Трехслойная стенка.
- •22 Теплопередача при изменении агрегатного состояния вещества.
- •23 Эффективное излучение поверхности.
- •24 Сложный теплообмен.
- •25 (Возможно не верно) Простейшая методика подбора теплоотвода для охлаждения полупроводниковых приборов (ост 4 го.010.030):
- •26 Системы охлаждения рэа.
- •27 Эффект Пельтье
- •28 Тепловые трубы.
- •29. Системы воздушного охлаждения.
- •2.Kopпyс с перфорацией.
- •30. Рекомендации по конструированию систем охлаждения.
- •Pэa о общей принудительной вентиляцией.
- •2. Рэа с принудительной внутренней циркуляцией воздуха.
- •Жидкостное охлаждение.
- •31. Основные характеристики и принципы построения систем принудительного типа для охлаждения рэс. Виды и основные характеристики теплообменников
- •32. Гидравлические характеристики аппарата и нагнетателя. Выбор нагнетателя Характеристики нагнетателя.
- •Определение рабочей точки и выбор нагнетателя.
- •Принцип суперпозиции.
14 Определение инерционных параметров.
mi - масса – инерционный параметр системы при поступательном движении;
Ixx, Iyy, Izz – моменты инерции при поворотном движении;
m – определяется суммирование масс различных частей, узлов, деталей блока.
г де Iii – собственный момент инерции всего блока относительного его центральных осей. Они определяются следующим образом:
– сумма собственных моментов инерции элементарных блоков относительно центров координатных осей этих блоков. Учитывая, что блоки простейших форм, их моменты инерции рассчитываются по таблицам.
– дополнительные моменты инерции, создаваемые блоком относительно координатных осей X, Y или Z .
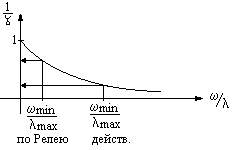
15 Неравенство Релея
Неравенство Релея:
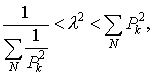
![]() –
собственная частота
системы.
–
собственная частота
системы.
![]() –
одна из 6-ти парциальных
частот:
–
одна из 6-ти парциальных
частот:
![]()
под знаком суммы могут присутствовать только разные парциальные частоты.
![]() –
количество слагаемых,
которое зависит от конструктивных
особенностей системы амортизации, как
справа, так и слева участвуют одни и те
же парциальные частоты.
–
количество слагаемых,
которое зависит от конструктивных
особенностей системы амортизации, как
справа, так и слева участвуют одни и те
же парциальные частоты.
Неравенство Релея позволяет определить диапазон собственных частот системы без точного определения конкретных частот, причем чем больше N, тем меньше точность в определении частот.
Расширение диапазона собственных частот при расчете по неравенству Релея обеспечивает дополнительный запас по значению коэффициента динамичности.
16 Определение собственных частот системы виброизоляции через парциальные частоты
Если в системе амортизации с 6-ю степенями свободы зафиксировать 5 степеней, то оставшаяся степень будет характеризоваться своей парциальной частотой. Т.о. для системы из 6-ти парциальных частот три частоты определяют поступательное движение объекта вдоль оси координат X, Y, Z и три частоты определяют поворотное движение объекта вокруг координат X, Y, Z.
P
– парциальная частота.
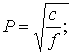
Парциальные частоты в поступательные:
|
m – масса объекта; |
Парциальные частоты поворотные:
|
|
Как видно из формул, расчет этих частот не представляет труда, если известны параметры системы.
17 Электрическое моделирование системы виброизоляции
Электромеханические аналогии.
Аналоговое моделирование базируется на изоморфизме (равноструктурности) дифференциальных уравнений, описывающих динамику механической систему и ее электрические модели.
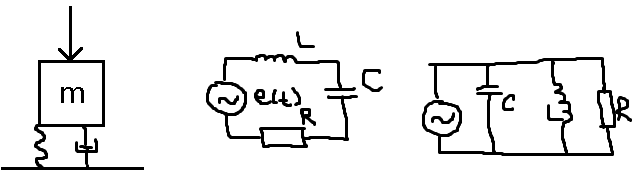


Для второй аналогии (сила-ток) – масса соответствует емкости.
Статическое электричество используется для:
Конденсаторных микрофонов (отличаются высочайшим качеством звука, равномерностью, большим частотным диапазоном, высокой чувствительностью).
18. Статический расчет системы. Определение координат центра тяжести объекта.
Исходным при проектировании системы амортизации являются не только параметры внешних механических воздействий, но и законченная компоновка устройства, т.е. считаются известными габариты устройства (блока), место установки, габариты, масса различных частей блока (узлы, детали), кроме этого существуют ограничения на типоразмер амортизатора. Необходимым является наличие всех характеристик для применяемого типа амортизатора.
На первом этапе в блоке аппаратуры выделяются элементарные узлы простейшей геометрической формы. При этом из сборочного чертежа всегда можно определить координаты центра тяжести этого элементарного блока относительно любой выбранной первоначальной системы координат. Для элементарного блока координаты его центра тяжести должны быть достаточно просто определяемыми. Рекомендуется первоначально выбирать систему так, чтобы одна ось проходила через ребро куба.
Определение реакций амортизаторов.
Различают две схемы нагружения амортизаторов: а) однонаправленная схема; б) пространственная схема нагружения.
а) Однонаправленная схема нагружения должна отвечать следующим условиям:
реакция виброизоляторов и нагрузка на них образуют систему параллельных сил;
блок в положении равновесия должен устанавливаться без перекосов;
г де G - суммарный вес блока, Pi -реакции амортизаторов.
Эта система возможна при установке блоков без перекосов.
В однонаправленной схеме нагружения неизвестной является реакция амортизатора и число неизвестных зависит от количества амортизаторов. Реакции виброизоляторов определяются на основе уравнений статистики. Для однонаправленной схемы:
|
My = 0; Mx = 0; n – число амортизаторов; |
При n = 3, ищем P1, P2, P3, (система из 3-х уравнений). При n = 3 система статически определима, и мы из исходной системы непосредственно находим три неизвестных реакции. При n = 4 система статически неопределима и необходимо четвертое уравнение. Его получают за счет введения дополнительного условия на расположение амортизаторов.
Дополнительные условия задаются за счет соответствующего выбора координат установки амортизаторов. Для такой системы P1 = P2 = P3 = P4 = G/4 . Здесь дополнительное условие – симметрия виброизоляторов – вылилось в подобное решение системы.
1. |
|
Всегда при и реакция P1 = P2 = … = Pn = G/n
2. Здесь дополнительное условие таково:
|
P1+P2 = P3+P4; (P1+P4)b’ = (P2+P3)b; P2 = P3; P1 = P4. |
Для того, чтобы система была статически определима необходимо задать n - 3 дополнительных условия!
б) Пространственная схема нагружения.
|
Это не однонаправленная схема (произвольное нагружение). Здесь кроме вертикальных нагрузок возникают составляющие по другим направлениям. Реакция – векторная сумма реакций по трем составляющим: Pi = {Pzi; Pxi; Pyi}.
|
Таким образом для пространственной схемы нагружения неизвестными являются не реакции, а составляющие реакций. При n амортизаторах имеем 3n неизвестных.
И з 6-ти уравнений определяем 6 неизвестных. Т.о. число дополнительных условий, которое необходимо задать 3n –6. Дополнительные условия получаем аналогично как и для схемы а).
Итак, считаем, что нам известны либо реакции (для схемы а), либо составляющие реакций (схема б). На этом расчет закончен.