Свойства дифференциала.

Если u = f(x) и v = g(x)- функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:

1. d(u  v) = (u  v)dx = udx  vdx = du  dv

2. d(uv) = (uv)dx = (uv + vu)dx = vdu + udv

3. d(Cu) = Cdu

Приближенные вычисления с помощью полного дифференциала.

Пусть функция f(x, y) дифференцируема в точке (х, у). Найдем полное приращение этой функции:

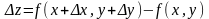
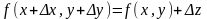
Если подставить в эту формулу выражение

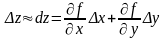
то получим приближенную формулу:

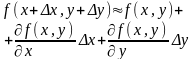
47. Производная и дифференциал сложной функции.

Производная сложной функции.

Теорема. Пусть y = f(x); u = g(x), причем область значений функции u входит в область определения функции f.

Тогда

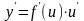
Доказательство.

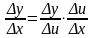
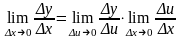
( с учетом того, что если x0, то u0, т.к. u = g(x) – непрерывная функция)

Тогда 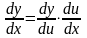. Теорема доказана.

Дифференциал сложной функции.

Инвариантная форма записи дифференциала.

Пусть y = f(x), x = g(t), т.е у- сложная функция.

Тогда dy = f(x)g(t)dt = f(x)dx.

Видно, что форма записи дифференциала dy не зависит от того, будет ли х независимой переменной или функцией какой- то другой переменной, в связи с чем эта форма записи называется инвариантной формой записи дифференциала.

Однако, если х- независимая переменная, то

dx = x, но

если х зависит от t, то х  dx.

Таким образом форма записи dy = f(x)x не является инвариантной.

48.Правила дифференцирования. Производные основных элементарных функций. Логарифмическое дифференцирование.

Основные правила дифференцирования.

Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х.

1) (u  v) = u  v

2) (uv) = uv + uv

3)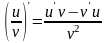 , если v  0

Эти правила могут быть легко доказаны на основе теорем о пределах.

Производные основных элементарных функций.

1)С = 0; 9)

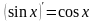
2)(x^m) = mx^m-1;

10)

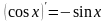
3)

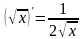
11)

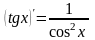
4)

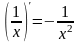
12)

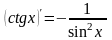
5)

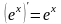
13)

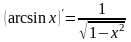
6)

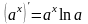
14)

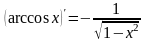
7)

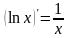
15)

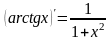
8)

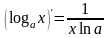
16)

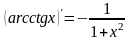
Логарифмическое дифференцирование.

Рассмотрим функцию .

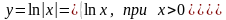Тогда (lnx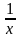)= , т.к. .

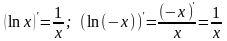Учитывая полученный результат, можно записать .

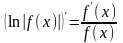Отношение 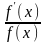называется логарифмической производной функции f(x).

Способ логарифмического дифференцирования состоит в том, что сначала находят логарифмическую производную функции, а затем производную самой функции по формуле

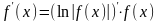
Способ логарифмического дифференцирования удобно применять для нахождения производных сложных, особенно показательных функций, для которых непосредственное вычисление производной с использованием правил дифференцирования представляется трудоемким.

49. Производные и дифференциалы высших порядков. Производная параметрически заданных функций.

Производные и дифференциалы высших порядков.

Пусть функция f(x)- дифференцируема на некотором интервале. Тогда, дифференцируя ее, получаем первую производную

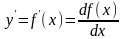
Если найти производную функции f(x), получим вторую производную функции f(x).

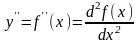
т.е. y = (y) или .

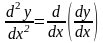Этот процесс можно продолжить и далее, находя производные степени n.

.

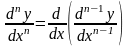Производная функции, заданной параметрически.

Пусть

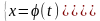
Предположим, что эти функции имеют производные и функция x = (t) имеет обратную функцию t = Ф(х).

Тогда функция у = (t) может быть рассмотрена как сложная функция y = [Ф(х)].

т.к. Ф(х) – обратная функция, то

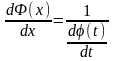
Окончательно получаем:

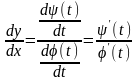
Таким образом, можно находить производную функции, не находя непосредственной зависимости у от х.

50. Теоремы о среднем. Правило Лопиталя-Бернулли. Формулы Тейлора и МакЛорена.

Теорема Роля: Если функция f(x) непрерывна на отрезке [a,b], дифференцируема на интервале (a,b) и на концах отрезка принимает одинаковые значения f(a)=f(b), то найдется хотя бы одна точка 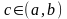, в которой производная 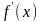обращается в ноль, т.е. .

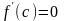Теорема Коши: Если функции f(x) и 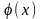непрерывны на отрезке [a,b], дифференцируемы на интервале (a,b), причем 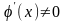для 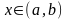, то найдется хотя бы одна точка , такая, что выполняется равенство .

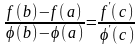Теорема Лагранжа: Если функция f(x) непрерывна на отрезке [a,b], дифференцируема на интервале (a,b), то найдется хотя бы одна точка такая, что выполняется равенство 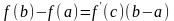. Это так же является формулой о конечном приращении: приращение дифференцируемой функции на отрезке [a,b] равно приращению аргумента, умноженному на значение производной функции в некоторой точке этого отрезка. Если производная функции равна нулю на некотором промежутке, то функция постоянна на этом промежутке. Если две функции имеют равные производные на некотором промежутке, то они отличаются друг от друга на постоянное слагаемое. Правило Лопиталя (по раскрытию неопределенностей вида 0/0) : Пусть функции f(x) и непрерывны и дифференцируемы в окрестности точки 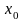и обращаются в ноль в этой точке: f( )=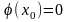 . Пусть в окрестности точки . Если существует предел 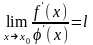, то .

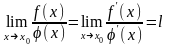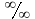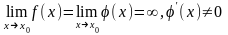Правило Лопиталя (по раскрытию неопределенностей вида ) : Пусть функции f(x) и непрерывны и дифференцируемы в окрестности точки (кроме, может быть, точки ), в этой окрестности . Если существует предел .
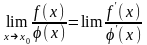