Задача №2

В таблице 6.5 даны горизонтальные проложения S_i и дирекционные углы α_i. Известны средние квадратические ошибки и . По одному из вариантов вычислить приращения координат по формулам:

,

и их средние квадратические ошибки:  и  .

Указание: см. решение задач 2.1 и 2.2 по формуле  раздела II.

Таблица 6.5
№ варианта	Si (м)	α i	№ варианта	Si (м)	α i
1	180,04	32°30,0′	6	160,39	66°33,9′
2	165,48	43°45,0′	7	209,74	41°52,6′
3	178,85	34°10,5′	8	176,89	34°12,9′
4	187,57	55°22,4′	9	182,72	48°38,0′
5	192,44	37°48,6′	10	168,09	56°18,0′

Задача №3

Даны результаты многократных независимых равноточных измерений одного и того же угла. Выполнить математическую обработку данного ряда:

1. Определить простую арифметическую средину;

2. Вычислить среднюю квадратическую ошибку отдельного результата измерений (по формуле Бесселя);

3. Определить среднюю квадратическую ошибку арифметической средины;

4. Построить доверительный интервал, накрывающий истинное значение угла с вероятностью 0,90.

Указания:

1. каждый студент не принимает в обработку три результата измерений, номера которых равны: i, , , где i — последняя цифра шифра (если последняя цифра 0, то следует принять );

2. все вычисления необходимо выполнять в соответствии со схемой решения задачи 3.1 раздела II (среднее значение угла округлить до десятых долей сек.).

Таблица 6.6
№ п/п	результаты измерений, хi	№ п/п	результаты измерений, хi	№ п/п	результаты измерений, хi
1	60°14′20,2″	5	60°14′20,4″	9	60°14′20,9″
2	22,8″	6	23,8″	10	22,5″
3	21,9″	7	24,2″	11	24,1″
4	20,8″	8	21,3″	12	21,8″

Задача №4

Даны результаты многократных независимых неравноточных измерений одного и того же расстояния (одним и тем же прибором, в примерно одинаковых условиях, но разным числом приёмов).

Выполнить математическую обработку данного ряда:

1. Вычислить общую арифметическую средину;

2. Определить среднюю квадратическую ошибку измерения с весом, равным единице;

3. Определить среднюю квадратическую ошибку наиболее надёжного значения;

4. Построить с вероятностью 0,90 доверительный интервал для истинного значения расстояния.

Таблица 6.7
№ п/п	результаты измерений xi (м)	число приёмов ni	№ п/п	результаты измерений xi (м)	число приёмов ni	№ п/п	результаты измерений xi (м)	число приёмов ni
1	204,282	3	5	204,284	5	9	204,285	2
2	,292	2	6	,289	4	10	,271	6
3	,274	6	7	,277	3	11	,288	4
4	,276	4	8	,278	5	12	,293	2

Указания:

1. каждому студенту необходимо исключить из таблицы 6.7 по три результата измерений с номерами: i, , , где i — последняя цифра шифра (если последняя цифра 0, то следует принять ), т.е. каждому студенту следует взять в обработку по девять результатов измерений;

2. все вычисления следует выполнять в соответствии со схемой решения задачи 4.3 раздела II;

3. веса отдельных результатов измерений следует принять пропорциональными числам приёмов: , где .
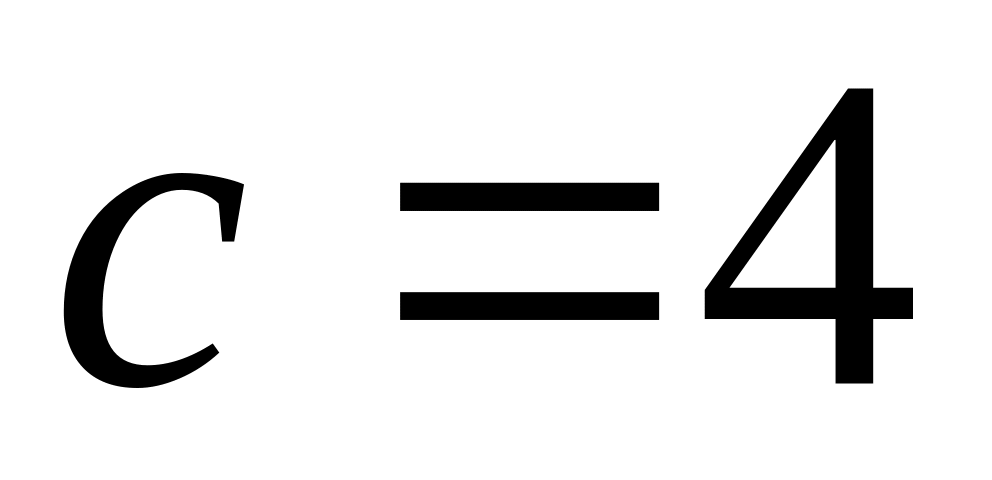