15. Логарифмические частотные характеристики.

При практических расчетах АСР удобно использовать частотные характеристики, построенные в логарифмической системе координат (логарифмические частотные характеристики – ЛЧХ). Они характеризуются большей линейностью и на определенных участках изменения частот могут быть заменены прямыми линиями и в целом представлены ломаными линиями. Причем отрезки прямых в большинстве случаев можно построить при помощи некоторых простых правил. Кроме того, в логарифмической системе координат легко находить характеристики различных соединений элементов, т.к. умножению и делению обычных характеристик соответствует сложение и вычитание ординат логарифмических характеристик.

За единицу длины по оси частот ЛЧХ принимается декада. Декада – интервал частот, заключенный между произвольным значением   и его десятикратным значением. Отрезок, соответствующий одной декаде, равен 1.

Обычно в расчетах используют логарифмическую амплитудную частотную характеристику (ЛАЧХ)

, дБ,                             (86)

ординаты которой измеряют в логарифмических единицах – белах или децибелах (0,1 бела), сокращенно дБ (рис. 23).

Бел – единица измерения отношения мощности двух сигналов. Если мощность одного сигнала больше мощности другого в 10 раз, то эти мощности отличаются на 1 Б (lg10 = 1).

Т.к. мощность сигнала пропорциональна квадрату амплитуды  ,то

или

.

При построении фазовой частотной характеристики логарифмический масштаб применяется только для оси абсцисс.

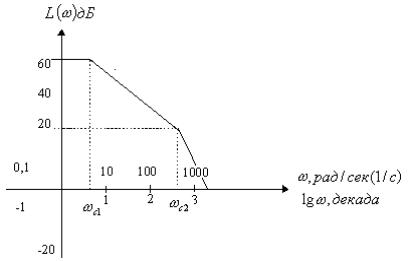
Рис. 23. Логарифмическая амплитудно-частотная характеристика

16. Передаточные функции

Передаточная функция - выведенное идеальное (теоретическое) соотношение между входным и выходным сигналом. Устанавливает взаимосвязь между выходным электрическим сигналом датчика S и  внешним воздействием : S =f(s). Представляется в виде: таблицы, графика, математического выражения.

Может быть линейной и нелинейной (например, логарифмической, экспоненциальной или степенной). Во многих случаяхпередаточная функция является одномерной (т.е. связывает выходной сигнал только с одним внешним воздействием).

Одномерную линейную функцию представляют в виде выражения:

S=a + bs,                     (3.1)

где а - постоянная составляющая (т.е. значение выходного сигнала при нулевом входном воздействии), b — наклон прямой, который часто называют чувствительностью датчика. s -  характеристика электрического сигнала, которую системы сбора данных воспринимают в качестве выходного сигнала датчика. В зависимости от свойств датчика это может быть амплитуда, частота или фаза.

Основные виды передаточных функций:

• логарифмическая: S = a + bln(s),

• экспоненциальная 

• степенная: 

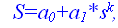
где к — постоянное число.

Если датчик имеет передаточную функцию, которую невозможно описать выше приведенными аппроксимирующими выражениями, то для него  применяются полиноминальные аппроксимации более высоких порядков.

Для нелинейных передаточных функций чувствительность b не является константой. Во многих случаях нелинейные датчики могут считаться линейными внутри ограниченного диапазона значений. Для более широкого диапазона значений нелинейная передаточная функция представляется в виде отрезков нескольких прямых линий: используется кусочно-линейная аппроксимация.

Для того, чтобы определить, может ли данная передаточная функция быть представлена в виде линейной зависимости, наблюдают за изменением выходных сигналов в линейной и реальной моделях при постепенном увеличении входного сигнала. Если разность сигналов не выходит за допустимые пределы, передаточную функцию данного датчика можно считать линейной. В случаях, когда на выходной сигнал датчика оказывают влияние несколько внешних воздействий, его передаточная функция становится многомерной. Примером датчика с двумерной передаточной функцией является инфракрасный датчик температуры. Его передаточная функция:

где G– константа, связывает две температуры: Ть — абсолютную температуру объекта измерения и Тs — абсолютную температуру поверхности сенсорного элемента с выходным напряжением..

.