Свойство условно сход.Ряда. (теорема римана)

Если ряд сходится условно, то в результате перестановки его членов можно получить ряд имеющий любую наперед заданную сумму, а так же расходящийся ряд.

Исследование знака переменных рядов на сходимость.

– знакопеременный

1. Проверить необходимый признак сходимости ряда

выполняется невыполняется (значит ряд расх.)

2. Проверяем абсолютную сходимость ряда.

-сходится

расходится сходится (сходимость абсолютн)

3. Проверим условную сходимость для проверки будем использовать 2 признака

- признак Лейбница

∑ аn n аn* аn+1<0

Сход (только знакочеред) n |аn+1|< |аn|

- признак Абеля

- ∑ аn – сходится

сходится

-( bn) –огранич (для любых численных рядов)

Пример: Исследование на сходимость

– знакопеременный

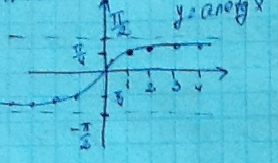
arctngn-? при n→∞

(arctngn)

arctngn→

Следовательно последовательность (arctngn) является возрастающей, ограничена сверху и при n→∞, arctngn→

1. Необходимый признак

(ОГР/б.б=б.м)

2)Абс.сход.

=

Сравним с рядом расходится = ( )= (arctgn)= неравный 0

Ряды ведут себя одинаково, СЛЕДОВАТЕЛЬНО

3. Условия сходимости

- ….. следовательно и ОГР

…. Ряд сходится, следовательно р.Лейбница и

Сх.Абеля

данный ряд сходится условно, так как он сходится, но не абсолютно.

11.Функциональные ряды.

Пример: x+x в квадрате/2+ x в кубе/3+х в 4-й степени/4+….и т.д.=

Sinx+sin2x+sin3x+…=

- + - + -….=

2n-четные

Функциональные ряды- последовательность, функций вместе с фиксированным порядком их суммирования.

Обозначение: (x)= (x)+ (x)+ (x)+ и т.д.

Пример: Рассмотрим ряд

А)Если подставить в этот ряд х=1 получим:

=1+ + + и т.д.- гармонический ряд расходится потому что:

-сумма геометр.прогрессии, <1-сходится, >=1-расходится

-огр альфа больше 1-сходится, альфа меньше или равно 1-расходится

Б) Если х=-1, то =-1+ - + ряд знакочередующийся

убывает, стремится к 0, при n, стремящемся к бесконечности, сл-но это ряд Лейбница, поэтому сходится

Если будет + - то расходится

Данный ряд Сходится условно, т.к. сумма эта большая Е -расходится

Пусть х= , тогда * = = + + ……

< - сходится, т.к. из сходимости большего следует сход-ть меньшего. Тогда исследуемый ряд сходится так же по 1 признаку сравнения.

Х=2, тогда = 2+ + + +…

стремится к бесконечности при n стремящемся к 0. Не выполняется необходимый признак сходимости ряда, следовательно ряд расходится.

Примечание: подставляем в функциональный ряд (x) конкретные значения аргумента от х= будем получать конкретные числовые ряды, которые могут быть знакоположительными и знакопеременными. Первые могут как сходиться так и расходиться, вторые же - могут сходиться как условно, так и абсолютно.

Определение: Множество всех точек (значениях х), в которых сходится функциональный ряд от х называется ОБЛАСТЬЮ СХОДИМОСТИ ФУНКЦИОНАЛЬНОГО РЯДА.

Х-область сходимости функционального ряда.

Алгоритм исследования функционального ряда на сходимость:

1. Фиксируем х. Рассматриваем ряд (x) как числовой.

2. Поиск условия сходимости. Рассматривается ряд, т.е. исследуем на сходимость, используя признаки сходимости знакоположительных рядов (Даламбер, Коши, признаки сходимости)

3. Определение интервала сходимости и исследование поведения ряда на границах интервала.

4. Запись области сходимости с учетом граничных точек.

Пример: исследуем на сходимость

1)Пусть х - фиксированное число, при подстановке этого числа, функциональный ряд превратиться в числовой. Очевидно, что при различных х ряд может оказаться и знакополож. И знакопеременным. Поэтому исследуем его сначала на абсолютную сходимость.

2) = знакоположительный, если >1, то =

След-но ряд расходится, т.к. не выполняется необходимый признак сходимости ряда.

Если модуль по х меньше 1, то сравниваем меньше чем как сумма гометр.прогрессии модуль g меньше 1.

По 1-му признаку сравнения из сходимости меньшего следует сходимость большего, значит ряд сходится абсолютно.

3) Интервал сходимости в точках от -1 до 1 ряд сходиться абсолютно. От бесконечности до -1 и от 1 до бесконечности ряд расходится.

Исследуем поведение ряда на границах интервала сходимости

Х=1 сумма вверху бесконечности внизу n=1 1/n-расходится, гармонический ряд

Х=-1 такая же сумма (-1) в степени n/n-ряд Лейбница, сходится. По модулю этот ряд будет расходится, а сл-но сумма по модулю -1 сходится условно

В итоге область сходимости ряда от квадратн.скобка -1 до 1).

12.Степенной ряд, свойства степенных рядов. Место для формулы.

Степенной ряд называют ряд вида a _n (𝞴-𝞴₀)ⁿ где ₀=const, (a_n) – числовая последовательность.

Пример: 𝞴 ⁿ / n! = 1+ x + x²/ 2! + x³/ 3!

0 !=1 1!=1

(𝞴-2)ⁿ / n² = x-2 + (x-2)²/ 4 +(x-2)³/ 0+

Центр и радиус сходимости степенного ряда.

П рим: Интервал сходимости степенного ряда всегда симметричен относительно точки 𝞴₀ называют центром степенного ряда.

𝞴₀

𝞴₀ – центр степенного ряда

R –радиус интервала сходимости

Вывод формулы R сходимости степенного ряда.

1шаг: Рассмотрим ряд с нулевым центром a_nxⁿ

Исследуем этот ряд на абсолютную сходимость по признаку Даламбера

d= |u_n+1( )/ u_n(𝞴 )|= a_n+1 𝞴^N+1/a_nxⁿ = |a_n+1*xⁿ*x/ a_n xⁿ| = |x| |a_n+1/ a_n |

Условия сходимости : d < 1

|x| |an+1/ a_n |< 1

|x|< |a_n/ a_n+1| =>R

Интервал сходимости.

- R 0 R

Где R = |a_n+1/ a_n |

2 шаг: Рассмотрим произвольную центром 𝞴₀

a_n (𝞴-𝞴₀)ⁿ

Обозначим t= (𝞴-𝞴₀)ⁿ , тогда a_n (x-x₀)ⁿ= a_ntⁿ этот ряд сходится на интервале |t| <R, где R вычисляем по формуле (*) (R> |a_n/ a_n+1| )

-R <t<R

-R < 𝞴- x₀<R

𝞴₀ – R< 𝞴<R+ 𝞴₀ или | x-x₀|<R

Вывод: интервал сходимости степенного ряда представляет собой окрестность точки 𝞴₀ радиуса R где R вычисляется по формулам

(*) R= |a_n/ a_n+1| - следствие признака Даламбера

(*) R= | 1/ |a_n| - следствие признака Каши