Раздел 2: векторная алгебра

Тема 1. Векторы в пространстве

10. Понятие вектора

Скалярная величина (скаляр) определяется только числом, которое показывает сколько определенных единиц измерения характеризуют эту величину (длина, площадь, объем, масса, температура и др.). Величины, которые характеризуются не только числом, но и направлением – векторные (скорость, сила и др.)

Направленным отрезком называется отрезок определенной длины и определенного направления.

Вектор – направленный отрезок.

Вектором также называют упорядоченную пару точек.

Если конец и начало отрезка фиксированы, то вектор – связанный. Связанные вектора обозначают , если А – начало, В – конец.

Если для вектора определяют лишь направление и длину (без фиксированных начала и конца), то данные векторы называют свободными. Как правило их обозначают . Свободный вектор может перемещаться в пространстве без изменения своего направления и параллельно самому себе.

Модулем вектора (или ) называется длина отрезка, которая ему соответствует. Модуль – длина вектора. Обозначается .

Вектор, длина которого равна единицы называется единичным вектором или ортом. Как правило единичный вектор обозначают .

Вектор, длина которого равна рулю – нулевой вектор. Обозначается .

Всякий ненулевой вектор можно унормировать, т.е. создать для него единичный вектор

.

Два вектора коллинеарны (параллельны), если они лежат на одной или на параллельных прямых. Обозначают . Среди коллинеарных векторов различают сонаправленные (обозначают ) и противоположнонаправленными (обозначают ).

Два вектора называют равными, если один из них может быть получен из другого путем параллельного переноса.

Если рассматривать связанные векторы, то равенство двух векторов определяют как совпадение их начал и концов. Если рассматривать свободные векторы, то , если и .

Исходя из смысла векторов можно утверждать, что для всякого свободного вектора можно построить единственный связанный вектор с началом в точке А, такой, что .

Последнюю запись понимают: свободный вектор перенесен в точку А.

Векторы компланарные, если они лежат в одной плоскости или параллельны одной и той же плоскости.

Углом между векторами и называется наименьший угол, на который нужно повернуть один вектор, чтобы его направление совпало с направлением другого вектора. Обозначают .

Для нахождения угла между векторами (геометрически) их начала совмещают. Исчисляется в пределах .

Если , то векторы ортогональны (перпендикулярны), .

20. Линейные операции над векторами

К линейным операциям относятся умножение вектора на число и сложение (вычитание) векторов.

1. Сложение векторов

Чтобы сложить два вектора в пространстве (на плоскости) можно использовать геометрический метод треугольника или параллелограмма.

Допустим в пространстве заданы три вектора . Их сложение можно произвести по правилу параллелепипеда или ломанной.

При сложении векторов методом параллелепипеда их начала совмещают. Вектор-диагональ – сумма векторов, начало которого совпадает с началом векторов :

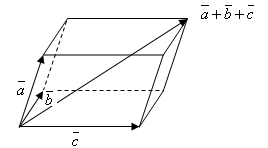
Сумму конечного количества векторов находят по правилу ломанной, которая необязательно лежит в одной плоскости. Вектор-сумма – вектор, соединяющий начало первого вектора с концом последнего.

Для операции сложения векторов справедливы свойства:

1. для всяких векторов существует единственный вектор ;

2. – коммутативность сложения;

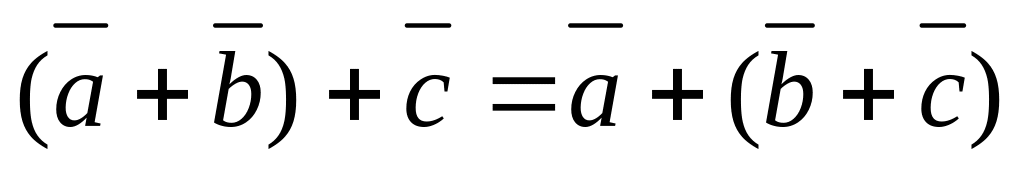3. – ассоциативность;

4. .