31. Винайдення логарифмів. Таблиці Непера.

Ще у 8 столітті індійський математик Вірасена розвинув концепцію ардхакчеди, що означала скільки разів число виду 2ⁿ можна поділити на два. Для чисел, які не є цілими спепенями двійки ардхакчеда залишалася невизначеною. Він описав також трікачеду та чатуртхачеду — відповідні числа для основ 3 і 4. 1544 року Міхаель Штіфель опублікував у Нюрнбергу книгу Arithmetica integra з таблицею цілих чисел і степеней двійки, які їм відповідають. Ці ранні дослідження можна вважати попередниками логарифмів.

Метод логарифмування був опублікований Джоном Непером у 1614 році в книзі під назвою Mirifici Logarithmorum Canonis Descriptio (Опис чудового правила логарифмів). Незалежно від Непера логарифми відкрив Юст Бурґі, але його публікація з'явилася на 6 років пізніше.

Непер не тільки сформулював правило множення чисел з використанням логарифмів, а й побудував перші логарифмічні таблиці. Методом повторного віднімання Непер обрахував 10⁷(1 − 10⁻⁷)^L для L від 1 до 100. Для L=100 результат приблизно дорівнює 0.99999 = 1 − 10⁻⁵. Далі він порахував добутки цих чисел при множенні на 10⁷(1 − 10⁻⁵)^L для L від 1 до 50, і, аналогічно, добутки цих числел при множенні на0.9995 ≈ (1 − 10⁻⁵)²⁰ й 0.99 ≈ 0.995²⁰. Обчислення тривали 20 років. Як наслідок він отримав число L, яке є розв'язком рівняння

для чисел від 5 до 10 000 000.

Спочатку Непер назвав L штучним числом, але потім запровадив новий термін — логарифм. У сучасній нотації з використанням натуральних логарифмів це співвідношення має вигляд^[8]

де наближення відповідає тому, що з дуже малою похибкою.

Дуже швидко винахід Непера здобув широке визнання. Роботи італійця Бонавентури Кавальєрі та німця Йоганна Кеплера розвинули і вдосконалили концепцію^[9]. 1620 року Едмунд Вінґейт збудував першу логарифмічну лінійку.

Натуральні логарифми були вперше описні Нікола Меркаром у праці Logarithmotechnia 1668 року^[10], хоча ще у 1619 вчитель математики Джон Спейделл складав таблицю натуральних логарифмів^[11].

Приблизно 1730 року Леонард Ейлер дав означення експоненти та натурального логарифма як

Ейлер показав, що ці функції обернені одна одній

32. Роботи братів Бернуллі.

Якоб Бернуллі (1654-1705) — швейцарський математик, основоположник теорій варіаційного числення і диференційних рівнянь.

Якобу Бернуллі належать значні досягнення в теорії рядів, диференціальному численні, варіаційному численні, теорії ймовірностей і теорії чисел, де його ім'ям названі числа з деякими певними властивостями (числа Бернуллі).

Якобу Бернуллі належать також роботи з фізики, арифметики, алгебри і геометрії.

Числа Бернулі — послідовність раціональних чисел   знайдена Якобом Бернуллі в зв'язку з обчисленням суми однакових степенів натуральних чисел:

,

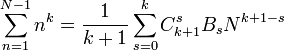де   — Біноміальний коефіцієнт.

Нерівність Бернуллі стверджує: якщо  , то

 для всіх 

У теорії ймовірності, формула Бернуллі дозволяє обчислити ймовірність успіхів у серії незалежних експериментів.

Якщо ймовірність   настання події   в кожному з випробувань стала, то ймовірність   того, що подія   настане   разів в   незалежних випробуваннях дорівнює

 

Йоганн Бернуллі (1667 —1748) —професор Гронінгенського (з 1695) і Базельського (з 1705) університетів, почесний член Петербурзької АН.

В 1648 відкрив експоненціальне числення.

Разом із братом Якобом розробляв аналіз нескінченно малих.

Йому належить перший друкований систематичний виклад інтегрального числення.

Вивів правило розкриття невизначеності типу 0/0, розробив методи інтегрування раціональних дробів, обчислення площ плоских фігур, випрямлення різних кривих, відкрив ряд, називаний його іменем і споріднений із рядом Тейлора, дав визначення поняття функції як аналітичного виразу, складеного зі змінних і постійних величин. Поставив класичне завдання про геодезичні лінії й знайшов характерну геометричну властивість цих ліній, а пізніше вивів диференціальне рівняння, що описує їх.

Повне зібрання його вчених праць з'явилося в Женеві (1742).