26. Основи інтеграційних методів Кеплера.

Обчислення секторіальних площ вимагало наявності вмінь користуватись нескінченно малими величинами, які вперше в практичній постановці запроваджено Й. Кеплером (мал. 1).

мал1.

Сутність методу Й. Кеплера полягає ось у чому. Щоб обчислити невідому площу (або об'єм), її розбивають на нескінченну множину нескінченно малих елементів однієї з нею розмірності, з цих елементів відповідною комбіна­цією утворюють нову площу (або об'єм), числове значення яких вміють обчислювати. Наприклад, коло складається з нескінченно великого числа нескінченно малих секторів, кожний з яких можна розглядати як рівнобедрений трикутник. Усі трикутники мають однакову висоту (радіус кола), а сума їх основ дорівнює довжині кола (мал. 2), Якщо в точці А провести до кола відрізок АВ дотичної довжини 2 π R, то сектори кола відкладуться в рівновеликі трикутники з тією самою висотою і основою, сума площ яких дорівнює площі ∆AOВ, тобто

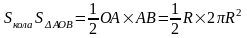
Свої інтеграційні методи Й. Кеплер запозичив з еврістичних міркувань Архімеда, але випускав етап доведення для більшої можливості маневрування методом, в результаті чого вони були не строгими і піддавались гострій критіці частиною математиків. Але перевага їх була в тому, що вони були новими, давали змогу розв'язати величезну кількість задач. Новизна і строгість рідко коли зживаються, особливо на ранніх етапах розвитку.

Мал. 2

27. Бонавентура Кавальєрі народився в 1958р. в Мілані, помер у Болоньї в 1947р. Сім'я Кавальєрі вважалася в Мілані старовинної і знатної, і молодий чоловік отримав прекрасну гуманітарну освіту, завдяки чому мав можливість читати в оригіналах античних математиків. З ранніх років родина Бонавентури призначала його до духовної кар'єри. У п'ятнадцятирічному віці він вступив до ордену іезуатов (не єзуїтів!). Патроном ордена вважався св. Ієронім.    Близько 1616г. Кавальєрі переїхав до Пізи, в монастир свого ордену, де продовжував освіту. Його керівником був Бенедикт Кастеллі, математик і астроном, учень Галілея, який і запропонував юному Бонавентурі зайнятися геометрією. За короткий час Кавальєрі вивчив твори Архімеда, Аполлонія й інших античних авторів. Учитель познайомив Кавальєрі з Галілеєм, і той деякий час керував заняттями молодого математика. У 1619г. Кавальєрі подав заяву сенату Болоньї про своє бажання зайняти кафедру математики. Тут він назвав себе "професором математики і учнем синьйора Галілея". На цей раз конкурс закінчився не на користь Кавальєрі. Він повернувся в Мілан, а потім жив у Флоренції, Римі, Пармі. У Римі він познайомився з Джованні Чіамполі, любителем точних наук і шанувальником Галілея. Вони швидко подружилися і зберегли назавжди найкращі стосунки. Кавальєрі присвятив Чіамполі головну працю свого життя "Геометрія" (1635г.). У присвяті автор писав на честь Чіамполі: "Це відкриття ... хоча і незначно, але ново, тобі (присвячую) як чоловікові, перевершив математичні науки стільки ж, скільки і всі інші".    У 1629г. Кавальєрі знову бере участь у конкурсі в Болоньї (кафедра астрономії). На цей раз його кандидатура потримати Галілеєм, Кастеллі, які підтверджували надзвичайно високе положення Кавальєрі серед математиків. У підсумку Кавальєрі зайняв кафедру. Він залишався на цій посаді до самої смерті. Папа Урбан IIX призначив його настоятелем монастиря, щоб забезпечити матеріально і надати можливість займатися наукою. Доля, здавалося б, дала Кавальєрі все, щоб зробити його життя щасливим: забезпечене почесне становище, прихильності "великих світу цього" (не тільки папа Урбан IIX, але слідували за ним папа Інокентій X не шкодували похвал своєму улюбленцю), можливість віддатися улюбленій справі ; любов і повагу друзів-людей, відомих у науці, нарешті, великі успіхи в обраній галузі математики та велика популярність. На жаль, він не був щасливий, його життя було безперервною боротьбою з хворобою. З юних років він страждав важкою формою подагри. З плином часу хвороба посилювалася. 30 листопада 1647г. черговий напад подагри призвів до трагічного кінця. На батьківщині Кавальєрі, в Мілані, йому поставлений пам'ятник.    У своїй основній праці "Геометрія" (1635г.) Кавальєрі розвинув розроблений ним задовго до виходу книги новий метод визначення площ і об'ємів-так званий метод неподільних. Неподільними Кавальєрі називав паралельні між собою хорди. Найважливіша ознака неподільності полягає в тому, що число вимірів його на одиницю менше самого геометричного образу. У плоскої фігури 2 виміру, у її неподільного, тобто у відрізка-1 вимір. Кавальєрі довів теорему про те, що площі двох подібних фігур відносяться як квадрати, а обсяги-як куби відповідних неподільних, і встановив, що відношення суми квадратів всіх неподільних трикутника до суми квадратів всіх неподільних паралелограма, що має з трикутником однакові підстави і висоту, дорівнює 1 : 3.    Згодом Кавальєрі знайшов аналогічні співвідношення для суми кубів і т.д. до дев'ятого ступеня неподільних. Праці Кавальєрі зіграли величезну роль у формуванні обчислення нескінченно малих.

Е. Торрічеллі (учень Г. Галілея і друг Б. Кавальєрі) поширив метод Кавальєрі на криволінійні неподільні. Свій метод не­подільних відпрацював незалежно від Б. Кавальєрі і на ал­гебраїчній основі Жіль Робервал (1604-1675). Про свої не­подільні він писав: "Можна вважати, що нескінченна множина точок приймається за нескінченну множину малих ліній і ста­новить цілу лінію. Нескінченна множина ліній являє собою не­скінченну множину малих площ, які складають всю площу. Не­скінченна множина площ являє собою нескінченну множину малих тіл, які усі разом складають все тіло" ("Трактат про не­подільні"). Це вже інше розуміння неподільних, ніж у Б. Ка­вальєрі, вони мають таку саму розмірність, як і утворена ними геометрична фігура, це крок до інтегральних сум.

28. Математики XVIII ст. працювали одночасно у області природознавства і техніки. Лагранж створив основи аналітичної механіки. Його праці показали, як багато результатів можна отримати в механіці завдяки потужним методам математичного аналізу. Монументальна праця Лапласа «Небесна механіка» підбила підсумки всіх попередніх робіт у цій області.

У цей часЭйлер увів у математику символ f(x) для функції і показав, що функціональна залежність є основним об'єктом вивчення математичного аналізу. Розроблялися способи обчислення частинних похідних, кратних і криволінійних інтегралів, диференціалів від функцій багатьох змінних.

У XVIII ст. з математичного аналізу виділилась низка дуже важливих математичних дисциплін: теорія диференційних рівнянь, варіаційне числення. Саме тоді почалася розробка теорії ймовірностей.

Ньютон зробив визначні відкриття; в галузі механіки, математики і астрономії. Усі найголовніші дослідження він провів у період перебування в Кембріджі. Одним з найвидатніших відкриттів Ньютона був метод обчислення нескінченно малих величин — «метод флюксій» (1665—1666 p.), остаточно оформлений і досконало викладений у вступі до трактату «Про квадратуру кривих» (видано лише в 1704 р. У цьому трактаті Ньютон пише, що він розглядає математичні кількості не як такі, що складаються з дуже малих сталих частин, а як такі, що утворюються неперервним рухом. Лінії описуються неперервним . рухом точок, поверхні — рухом ліній, об'єми — рухом поверхонь, кути — обертанням сторін і т. д. Він помітив залежність між швидкістю наростання «кількості» і «кількістю».

29. Готфрід Вільгельм Лейбніц — провідний німецький філософ, логік, фізик, математик, мовознавець та дипломат. Народився він 1 липня 1646-го року у Лейпцигу (Німеччина), помер 14 листопада 1716 року у Ганновері.

Саме Лейбніц передбачив принципи сучасної комбінаторики. Створив першу механічну лічильну машину, здатну виконувати додавання, віднімання, множення й ділення. Незалежно від Ньютона створив диференціальне й інтегральне числення і заклав основи двійкової системи числення.

У рукописах і листуванні, які було надруковано лише в середині XIX ст., Лейбніц розробив основи теорії детермінантів. Зробив вагомий внесок у логіку і філософію. Мав надзвичайно широке коло наукових кореспондентів. Багато з його ідей викладено в рукописах і листуванні, що ще й досі повністю не надруковані.

Біографія. У 1661-му році, у віці 14 років, Лейбніц вступив до Лейпцизького університету, де у 1663-му році отримав ступінь бакалавра, з дисертацією “De Principio Individui”, з якої бере початок його пізніша теорія монад.

Незважаючи на його неабияку на той час репутацію і визнання його праць, Лейбніцу було відмовлено у ступені доктора права в Лейпцигу, тому він негайно поїхав до Альтдорфа, де у лютому 1667 р. отримав цей ступінь за свою дисертацію “De Casibus Perplexis”. Йому була запропонована посада професора в Альтдорфі, але Лейбніц відмовився, обравши натомість кар’єру дипломата і юриста. У 1667-1672 роках перебував на службі Майнського курфюрста, барона Йоганна Кристіана фон Бойнебурґа, завдяки якому у 1672 р. він дістав змогу подорожувати до Парижа, де він залишатиметься до жовтня 1676 р., і до Лондона взимку 1673 р.

Під час цих подорожей Лейбніц познайомився з деякими найвидатнішими вченими і філософами того часу, зокрема Арно, Малебраншем і Гюйгенсом у Парижі, а також Гуком, Бойлем і Пеллем у Лондоні. Під час перебування у Парижі, Лейбніц розпочав дослідження з диференціального й інтегрального числення. Лейбніц надавав надзвичайну увагу питанням зручної наукової нотації, і в рукописі від 21 листопада 1675 р. він уперше використав нині загальновизнаний запис для інтегралу функції. З грудня 1676 р. до кінця свого життя Лейбніц обіймає посади надвірного бібліотекаря та канцлера у місті Ганновер.

Наукові досягнення. У 1671 р. Лейбніц надрукував мемуар “Hypothesis Physica Nova”, у якому намагався розробити абстрактну теорію руху. Слідом за Кеплером, стверджував, що рух залежить від дії духа.

Лейбніц шукає можливості для розширення наукових контактів. Він розпочинає листування з Ольденбургом, секретарем Лондонського наукового товариства. Восени 1672 р., з нагоди дипломатичної місії від Бойнебурга у Парижі, Лейбніц обізнається з Гюйгенсом і за його керівництвом розпочинає дослідження з теорії рядів і знаходить славетну формулу.

Під впливом Гюйгенса Лейбніц вивчає праці Паскаля, Грегорі та інших з інфінітезімальної геометрії, тобто питання дотичних до кривих, і виходить з ідеєю “функції”, в сучасній термінології — похідної, таким чином винаходячи центральну концепцію математичного аналізу.

Ньютон написав два листа до Лейбніца, в яких повідомив про свої дослідження з аналізу, але без викладання методів. У відповідь Лейбніц описав деякі зі своїх методів, щодо яких Ньютон зневажливо зауважив: “…не розв’язане жодне попередньо відкрите питання…”.

30. Еволюція поняття функції. Функція - одне з основних математичних і загальнонаукових понять. Воно зіграло й понині відіграє більшу роль у пізнанні реального миру.

Пропедевтичний період (з найдавніших часів до 17 століття).

Ідея функціональної залежності сходить до стародавності. Її втримування виявляється вже в перших математично виражених співвідношеннях між величинами, у перших правилах дій над числами. У перших формулах для знаходження площі й обсягу тих або інших фігур. Так, вавилонські вчені (4-5тис.років тому) нехай несвідомо, установили, що площа кругу є функцією від його радіуса за допомогою знаходження грубо наближеної формули: S=3r2.

Починаючи лише з 17 століття, у зв'язку із проникненням у математику ідеї змінних, поняття функції явно й цілком свідомо застосовується.

Шлях до появи поняття функції заклали в 17 столітті французькі вчені Франсуа Виет і Рене Декарт; вони розробили єдину буквену математичну символіку, що незабаром одержала загальне визнання. Уведене було єдине позначення: невідомих - останніми буквами латинського алфавіту - x, y, z, відомих - початковими буквами того ж алфавіту - a, b, c, ... і т.д. Під кожною буквою стало можливим розуміти не тільки конкретні дані, але й багато хто інші; у математику прийшла ідея зміни.

Крім того, у Декарта й Ферма (1601-1665) у геометричних роботах з'являється виразне подання змінної величини й прямокутної системи координат. У своїй “Геометрії” в 1637 році Декарт дає поняття функції, як зміна ординати крапки залежно від зміни її абсциси; він систематично розглядав лише ті криві, які можна точно представити за допомогою рівнянь, притім переважно алгебраїчних. Поступове поняття функції стало ототожнюватися, таким чином, з поняттям аналітичного вираження - формули. В 1671 році Ньютон під функцією став розуміти змінну величину, що змінюється із часом (називав в “флюентой”).

В “Геометрії” Декарта й роботах Ферма, Ньютона й Лейбница поняття функції носило по суті інтуїтивний характер і було зв'язано або з геометричними, або з механічними поданнями: ординати крапок кривих - функція від абсцис (x); шлях і швидкість - функція від часу (t) і т.п.

Аналітичне визначення функції (17 - початок 19 століття).

Саме слово “функція” (від латинського functio -здійснення, виконання) уперше було вжито німецьким математиком Лейбницем в 1673р. у листі до Гюйгенсу (під функцією він розумів відрізок, довжина якого міняється по якому-небудь певному законі), у пресі ввів з 1694 року. Починаючи з 1698 року, Лейбниц увів також терміни “змінна” і “константа”. В 18 столітті з'являється новий погляд на функцію як на формулу, що зв'язує одну змінну з іншої. Це так звана аналітична точка зору на поняття функції. Підхід до такого визначення вперше зробив швейцарський математик Иоганн Бернуллі (1667-1748), що в 1718 році визначив функцію в такий спосіб: “функцією змінної величини називають кількість, утворена яким завгодно спосіб із цієї змінної величини й постійних”.

В “Диференціальному обчисленні”, що вийшло у світло в 1755 році, Эйлер дає загальне визначення функції: “Коли деякі кількості залежать друг від друга таким чином, що при зміні останніх і самі вони піддаються зміні, те перші називають функцією других”. “Це найменування, - продовжує далі Эйлер - має надзвичайно широкий характер; воно охоплює всі способи, якими одна кількість визначається за допомогою інших”.

Як видно з певних визначень, саме поняття функції фактично ототожнювалося з аналітичним вираженням. Нові кроки в розвитку природознавства й математики викликали й подальше узагальнення поняття функції.