5. Суть расчёта на устойчивость

Основные понятия, определение устойчивости, формула Эйлера, подбор сечений сжатых стержней.

П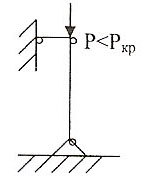 роводя расчёты на прочность и жёсткость при различных деформациях полагают, что во время деформацилюбой системы имеет место единственная заранее известная форма равновесия. В действительности же в деформированном состоянии равновесие между внешними и вызываемыми ими внутренними силами упругости может быть не только устойчивым, но и неустойчивым. Между этими двумя состояниями равновесия существует переходное состояние, называемое критическим.

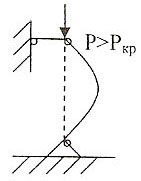Р авновесие называют устойчивым, если при любом малом отклонении от положения равновесия тело возвращается в исходное положение по устранении причины, вызвавшей это отклонение.

Равновесие называют неустойчивым, если при любом малом отклонении от положения равновесия тело не возвращается в исходное положении, а всё дальше отклоняется от него.

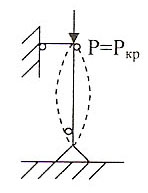
Равновесие называют критическим в том случае, если тело находится в безразличном равновесии: оно может сохранить первоначально приданную ему форму, но может и потерять её от самого незначительного воздействия.

Устойчивость формы равновесия деформированно­го тела зависит от величины приложенных к нему нагру­зок.

Нагрузка, превышение которой вызывает потерю устойчивости первоначальной формы тела, называется критической и обозначается Р_кр.

Формула для определения критической силы:

впервые была получена в 1744 Леонардом Эйлером, поэтому иногда её называют формулой Эйлера.

Р_кр представляет собой наименьшую сжимающую силу, при которой наряду с прямолинейной формой равновесия становится возможной другая (изгибная) форма рав­новесия.

Формула Эйлера получена в предположении шарнирного опирания стержня по концам. На практике встре­чаются и другие способы закрепления концов стержня, в связи с чем вводится понятие приведенной длины, l₀ = µ l, где µ - коэффициент приведенной длины.

К ритическая сила при различных способах опирания стержней может быть получена по обобщённой фор­муле

П одбор сечений сжатых стержней осуществляется по формуле

где σ_кр - нормальное напряжение в поперечном сечении сжатого стержня, соответствующее критическому значению сжимающей силы.

где λ - гибкость стержня и

Формула Эйлера справедлива при условии λ ≥ 100.

6.Статически неопределимые системы

Определение. Статически неопределимой системой называется система, определение усилий в которой невозможно с помощью одних, лишь уравнений статики, и поэтому для расчёта mama систем требуется составление дополнительных уравнений, учитывающих характер деформации.

К статически неопределимым относятся:

• Многопролетные неразрезные балки;

• Однопролетные балки с 1 или 2 защемляющими опорами;

• Арки двухшарнирные и бесшарнирные;

• Рамы;

• Фермы с лишними опорными стержнями (внешне статически неопределимые системы) или фермы с лишними собственными стержнями (внутренне неопределимые системы).

В статически неопределимой системе лишние связи, как внешние, так и внутренние, являются лишними с точки зрения обеспечения неизменяемости и равновесия системы, которая и без них может быть неизменяемой и находиться в равновесии. Постановка же таких связей вызывается конструктивными особенностями.

Любая статически неопределимая система характеризуется степенью статической неопределимости, которая может быть определена по формуле:

W = ЗК-Ш,

где W - лишние связи

К — количество замкнутых контуров

III - число простых и приведенных к ним сложных шарниров в замкнутых контурах.

Одним из методов решения статистически неопределенных систем является метод сил.