1. Сила, элементы графостатики

Момент силы. Система сил. Равнодействующая сил. Сложение сил. Перенос силы параллельно самой себе. Главный вектор и главный момент. Условия равновесия.

Тела в природе различным образом взаимодействуют между особой или с окружающей средой. Мера механического взаимодействия тел, т.е. взаимодействия, влияющего на их состояние покоя или движения, характеризуется силой.

Сила определяется:

• Числовым значением,

• Направлением,

• Точкой приложения.

Таким образом, сила - величина векторная.

Системой сил будем называть совокупность сил, действующих на одно рассматриваемое тело. Различают системы сходящихся, параллельных и произвольно-расположенных сил.

Если данная система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системы сил.

Величину, равную геометрической сумме сил ка­кой-либо системы, называют главным вектором этой сис­темы сил. Геометрическая сумма R‾ _гл, (главный вектор) любой системы сил определяется или последовательным сложением сил системы по правилу параллелограмма (или треугольника) или построением силового многоугольника.

Р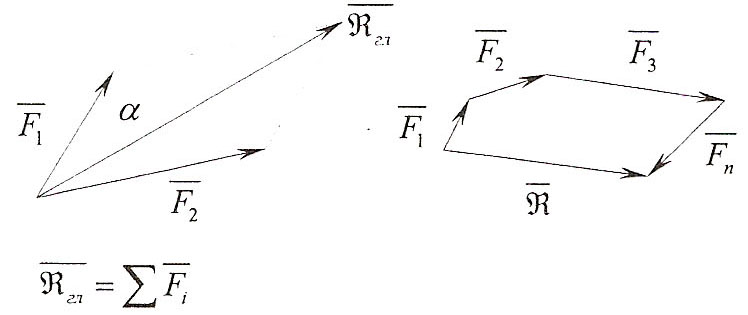 авнодействующая системы сходящихся сил находится непосредственно с помощью закона параллелограмма сил. Аналогичную задачу можно решить и для произвольной системы сил, если найти возможность перенести все силы в одну точку. Такая возможность существует. Перенесем силу F‾ из очки. А в точку В .

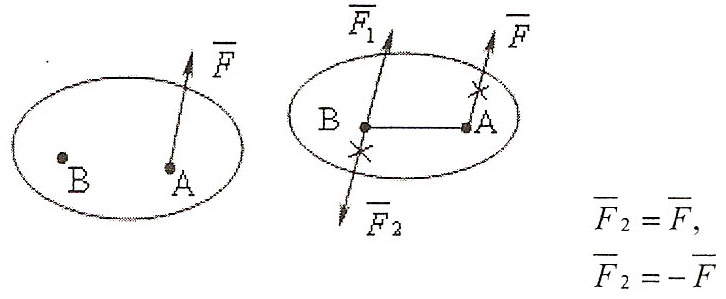
Полученная при этом система трёх сил и представляет собой силу F‾ ₁ = F, но приложенную в точке В, и пару F‾ ,F‾ ₂. (Парой сил называется система двух равных по мо дулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело).

Т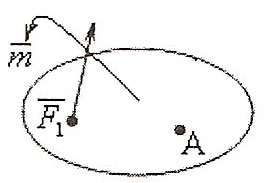 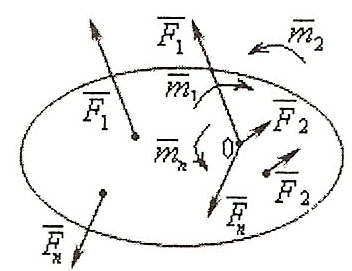аким образом, система произвольно расположен­ных сил при приведении к произвольно выбранному центру эквивалента одной силе R‾_гл (главному вектору), приложенной в центре приведения, и одной паре М‾_гл (главному моменту).

Отметим, что сила R‾_гл не является равнодействующей системы сил, т.к. заменяет систему сил не одна, а вместе с парой М‾_гл .

Для равновесия любой системы сил необходимо и достаточно, чтобы R‾_гл =0 и М‾_гл =0.

2. Хрупкость и пластичность

Определения хрупкого и пластичного материала. Напряжение. Виды напряжённых состояний. Диаграммы растяжения-сжатия. Закон Гука.

При проектировании строительных конструкций необходимо установить значения величин, характеризующих прочностные и деформативные свойства материалов. Наибольшую информацию о механических свойствах металлов можно получить из статических испытаний на растяжение. Записанные с помощью специального устройства диаграммы растяжения (т.е. графики зависимости между

растягивающей силой F‾ и удлинением образца ∆l) имеют

в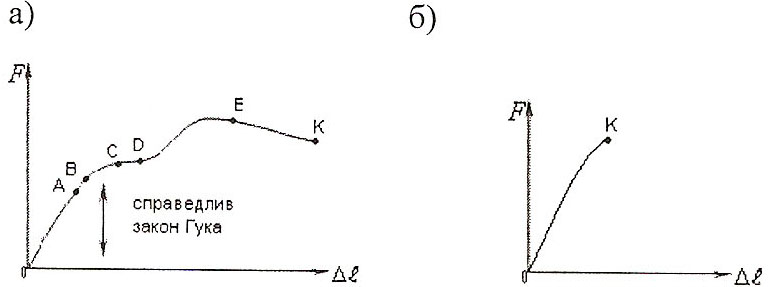 ид:

Первая диаграмма характерна для пластических материалов (низкоуглеродная сталь).

Диаграмма имеет ряд характерных участков: ОА - зона упругости, нагрузка пропорциональна деформации;

АВ - до точки В, в материале не обнаруживается признаков пластической (остаточной) деформации;

CD - площадка текучести, деформации растут практически без увеличения нагрузки;

BD - зона общей текучести, в этой зоне значительно развиваются пластические деформации.

DE - зона упрочнения, при максимальном (или не сколько меньшем) усилии на образце в наиболее слабом месте возникает сужение - «шейка»;

ЕК - зона местной текучести, деформации происходят в области «шейки» вплоть до разрыва в точке К.

Вторая диаграмма характерна для хрупкого мате риала (чугуна). Диаграмма не имеет выраженного начального прямолинейного участка. Разрыв образцов из хрупких металлов происходит при весьма незначительном удлинении и без образования шейки.

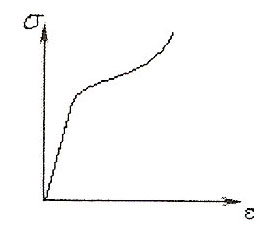
Диаграмма F = f (∆l) зависит от размеров образца, поэтому её перестраивают в координатах «напряжение-деформация».

Напряжением называется внутренняя сила, отнесённая к единице площади в данной точке рассматриваемого сечения σ =F/A . Изменение ∆l первоначальной длины

стержня l называется абсолютным удлинением. Отношение абсолютного удлинения к первоначальной длине

ε = ∆l/l называется относительным удлинением или деформацией.

При упругих деформациях связь между деформациями и напряжениями линейна и описывается законом Гука: σ = Е *ε , где Е - модуль упругости первого рода или модуль Юнга.

Испытание материалов на сжатие проводят на специальных прессах.

Испытанию на сжатие подвергают главным образом хрупкие материалы, которые, как правило, лучше сопротивляются сжатию, чем растяжению, и применяются для изготовления элементов, работающих на сжатие.

Диаграмма сжатия чугуна:

Для пластичных материалов модуль упругости Е, а также некоторые другие характеристики, примерно те же, что и при растяжении. Напряжение, соответствующее разрушающей силе, получить нельзя, т.к. образец не разрушается, а превращается в диск.

Диаграмма сжатия низкоуглеродной стали: