4.;8.Нормальное и аномальное маг. Поля

Г.п. и руды имеют неодинаков.магн.св-ва. Большая часть п. и руд относ-ся к слабомагн.или практически немагн. На участках зем.пов-ти где кора сложена только такими породами наблюдается нормальное магн. поле- невозмущённое, близкое к однород. Вертик.состав-я напряжения геомагнит.поля Z_o=2Mcos0/R3, горизонт.сост-я H₀=Msin0/R3, полная напряж-ть геомагн.поля T_o=(Z_o2+H_o2)=M/R3(1+3cos20) где 0-угол м/у осью земного магн.диполя и радиус-вектором, проведённым из центра земли в данную точку на её пов-ть. Геомагн.широта у=90-0. Полный вектор напряж-ти дипольного магн.поля Т₀ достигает наиб.значения на магн.полюсах (0=0) и наимен. значение магн.экваторе(0=90).Часть пород обладает повыш намагн-тью. Намагн.тела создают своё собственное магн.поле, к-рое наз-ся аномальным. Отклонение измерит.элементов геомагн.поля земли от элементов поля однород. наманг.сферы наз-ются магнитными аномалиями. По рез-там полевых измерений выч-ют следущие аномалии:модуля полного вектора напряж-ти дТa=Т-Тн;вертик.составляющей дZ=Z-Zн; горизонт.сост-я дНа=Н-На. При вычис-ии магн.аномалий в наблюд.значения необх.вносить поправки. Главной явл-ся поправка за измен-е геомагн.поля во времени, к-рую рассчитывают по рез-там непрерыв.регистрации во времени элементов геомагн.поля на спец.вариационных магн.станциях.

11. Решение прямой задачи магниторазведки для шара.

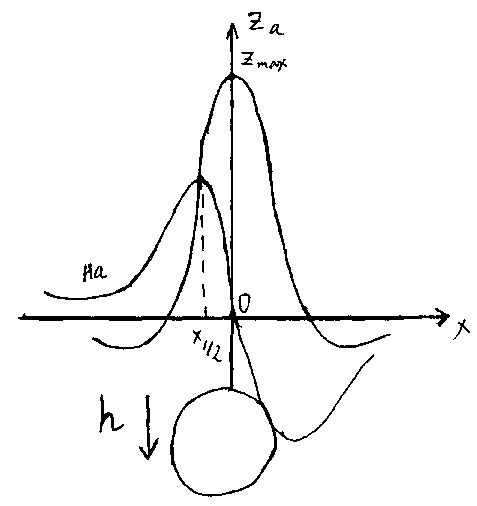
Поле шара можно вычислить как сумму полей отрицательного полюса, расположенного в близи центра в верхней половине сферы, и положительного полюса, расположенного в нижней ее половине. Центр сферы расположен на оси z глубине h. Найдем значения элементов магнитного поля в произвольной точке Р, находящейся на оси x. Согласно формуле Пуассона , где V-потенциал притяжения; G-гравитационная постоянная; -плотность тела. Учитывая выражения для гравитационного притяжения однородного шара данные выражения запишем в виде , где М-магнитный момент сферы M=J; J – интенсивность намагничивания;  - объем шара. Выполнив дифференцирование и простейшие преобразования получим; ; ;

12.Решение обратн задачи магниторазведки методом касательных.

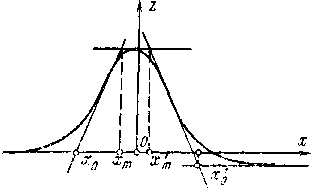На графике аномалий вертикальной составляющей Z, полученном вкрест простирания аномалии, проводят касательные (рис): в точке максимального значения, в двух точках минимальных значений и в двух точках перегиба. Глубину верхней кромки магнитовозмущающей массы вычисляют по экспериментальной формуле: , где x_m, x₀,x`<sub>m</sub>, x`₀- абсциссы точек пересечения касательных.

13.Решение обратной задачи магниторазведки для вертикально намагниченной сферы.

В случае вертикально намагн. сферы опред. магн. момент М, глубину залегания центра ξ и радиус R сферы. Задача нахождения радиуса сферы не имеет однозначного решения, т.к. он связан с магнитным моментом и интенсивностью намагничивания уравнением: . Поскольку аномалии Z и H вертикально намагниченной сферы опред-ся формулами, то решение обратной задачи будет аналогичным решению обратной задачи для аномалий вторых производных потенциала силы тяжести. По графику найдем Z. ξ= 0,7х₀ По известной глубине залегания центра сферы нетрудно определить магнитный момент сферы: . Глубина залегания центра сферы связана с графиком Н уравнением. То ξ= 2х_э. Зная глубину залегания центра сферы, найдем магнитный момент: . Для вычисления радиуса сферы необходимо знать полное значение вертик. составляющей Z` геомагнитного поля и магнитную восприимчивость æ сферы. Радиус сферы найдем из формулы: .

14.Методы решения обратной задачи магниторазведки.

Обратная задача- определение формы, размеров, положения в пространстве и характера намагничивания по данным измерениям магнитного поля. Решается аналитически и графически. Не имеет ед. решения. При выполнении количественной интерпретации, реальный геологический процесс обычно упрощают, идеализируют, заменяют моделью приближенно отражающую основные особенности разреза. Методы полной интерпретации магнитометрических данных делятся на несколько групп. Каждая группа определяется различной чувствительностью к случайным и систематическим погрешностям измерения, разной разрешающей способностью, трудоемкостью и точностью. Методы: метод характерных точек (касательных); интегральный метод; предельный или оценочный; амплитудный; методы сравнения; векторный; методы подбора; методы основанные на теории функции комплексного переменного.

При интерпретации суммарное наблюденное поле разделяют на отдельные составляющие. Разделение наз трансформацией. Способы: осреднение, способ вариаций, пересчет поля в нижнее полупространство.