9.Поправка за высоту точки наблюдения при обработке данных гравиразведки.

В нормальное значение силы тяжести вводят поправку за высоту. Притяжение масс, расположенных между физической поверхностью и уровнем моря, не учитывается. Поэтому данная поправка называется также поправкой за свободный воздух или поправкой Фая.

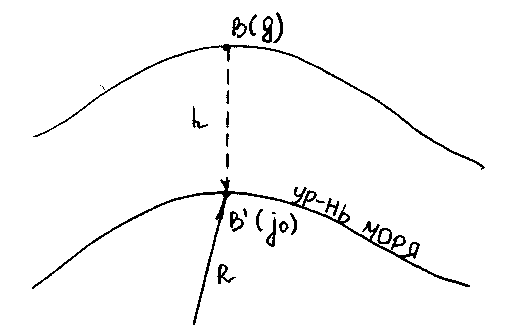
Нормальное значение силы тяжести

_о=fM/R² (для В’); g_о=fM/(R+h)² (для В).

f – гравитационная постоянная.

₁g=_о-g_о=fM[1/R²-1/(R+h)²]=(fM/R²)[1-(R/(R+h))²].

М – масса Земли; R –средний радиус Земли; h - превышение от­носительно уровня моря. Учитывая, что h не превосходит нескольких км, а R=6371км, примем ₁g=2_оh/R, где _о=981000мГал.

Тогда ₁g=0,3086h – поправка за высоту т. наблюдения.

Корректируя редукцию в свободном воздухе поля _о, получаем нормальное значение силы тяжести в т. наблюдения на высоте h: =_о- 0,3086h.

После введения поправки за высоту аномалия силы тяжести имеет вид

g_св.в.=g-=g-_о+0,3086h.

В этом случае мы пренебрегаем действием масс м/у т. наблюдения и уровнем моря. Эти массы увеличивают наблюденное значение силы тяж. Аномалия силы тяж. с поправкой за высоту зависит от высоты пункта наблюдения. Эта завис-ть делает их малопригодными для использования в геологических целях.

11.Дать определение нормального и аномального поля силы тяжести.

Нормальное – это поле силы тяжести на уровенной пов-ти теоретической Земли. Аномальное – разность наблюденного значения силы тяжести, приведенного к уровенной пов-ти и нормального значения поля силы тяжести.

Формула Клеро: у=уэ(1+бsin^2ф)

14.Методы решения прямой и обратной задач гравиразведки.

Прямая задача гр/р состоит в вычеслении гравитац эффектов, создаваемых различными избыточными массами. Решение прямой задачи всегда однозначно, т.е. при известной форме, глубины залегания и избыточной плотности возмущающей массы в каждой точки наблюдений можно вычислить едигственное значение силы притяжения.

Решение обратной задачи гр/р заключается в нахождении по заданым значениям аномалий силы тяжести или аномалий вторых производных потенциала сила тяжести избыточной массы, глубины залегания и конфигурации возмущаюжих тел и базируется на исходных выражениях, определяющих гравитационный эффект, создаваемый возмущаещими телами. Обратную задачу всегда решают приминительно к некот выбранной из априорных соображений гравиметрической модели реального геологического разреза.

15.Решение прямой задачи гравиразведки для шара.

Прямой задачей наз. расчет аномалий потенциала и его производных по известному распределению плотностных неоднородностей в з.к. Прямая задача для тел простейшей формы решается с помощью аналитических формул, которые получены из выражения для потенциала точечной массы. Для точки наблюдений, внешний по отношению к притягивающим массам (к шару), потенциал притяжения равен: V=fM/, где  - расстояние м-у притягиваемой точкой с координатами (X,Y,Z) и притягивающей точкой шара с координатами (,,), равное

f – гравитационная постоянная, f=6,67*10^-8 см³/г*с² (СГС)=6,67*10^-11м³/кг*с² (СИ); М – масса шара радиуса R, притяжение которого во внешнем пространстве равно притяжению точечной массы М=4/3*R³,  - избыточная плотность.

Вычисление аномального эффекта для шара производится по след. формулам:

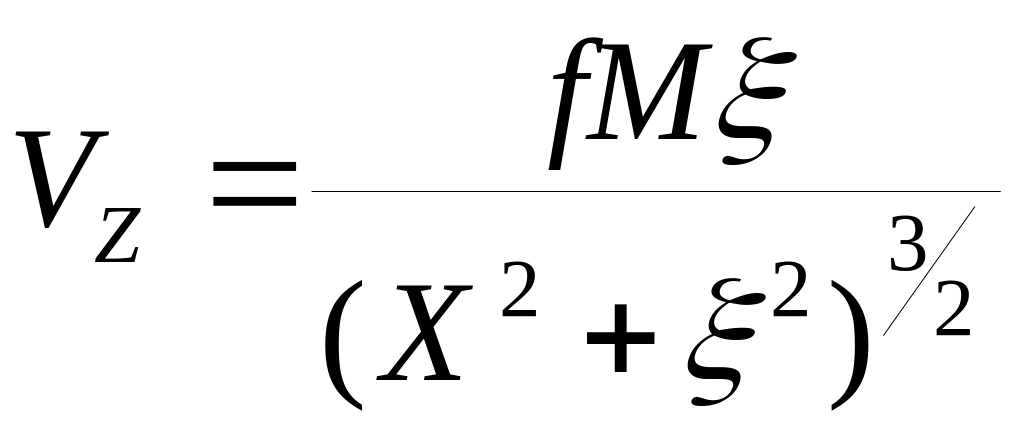
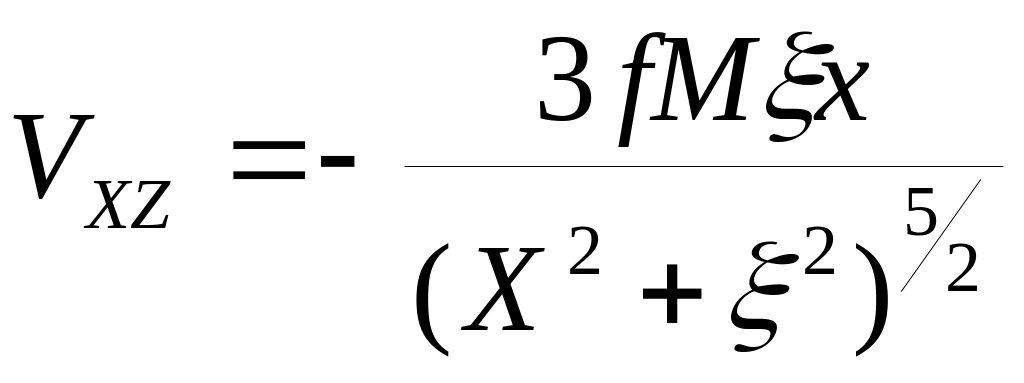
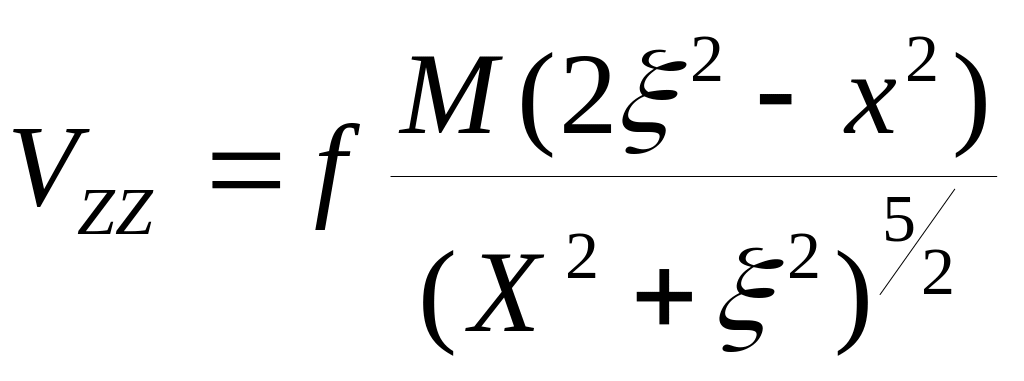
где V_Z, V_XZ, V_ZZ – производные гравитационного потенциала;  - глубина залегания тела.