1.3. Соединение (композиция) автоматов

Параллельное соединение

Пусть заданы два автомата Мили:

и .

Параллельное соединение возможно, если только = =V. Считаем также, что задано устройство , объединяющее выходы и реализующее функцию , представленную на рис.4. Для эквивалентного автомата Мили (рис.5) имеем выходной алфавит ,



множество состояний ,

функцию переходов , где , т.е. ,

функцию выходов , т.е.

и начальное состояние .

Пример 5. Пусть автоматы и заданы таблицами 4 и 5 соответственно, функция таблицей 6. Считаем, что = =₁ и = =₂.

Результирующий автомат характеризуется совмещенной таблицей переходов/выходов (табл.7).

Таблица 7

v1 v2	/ / / / / / / /

Последовательное соединение

Пусть задано последовательное соединение автоматов Мили и (рис.6). Предполагается, что выходной алфавит совпадает с входным алфавитом , т.е. :

Т огда для эквивалентного последовательного автомата Мили имеем:

множество состояний ,

функцию переходов

и функцию выходов .

Пример 6. Рассмотрим последовательные соединение автоматов и из примера 5. Считаем, что и . Тогда последовательное соединение и характеризуется совмещенной таблицей переходов/выходов (табл.8).

Таблица 8

v1 v2	/ / / / / / / /

1.4. Тестирование абстрактных автоматов

В основе тестирования (контроля и диагностики) конечных абстрактных автоматов лежит теория экспериментов с автоматами. Эксперимент над автоматами заключается в следующем:

• на вход автомата подается последовательность входных символов,

• фиксируется реакция автомата (последовательность выходных символов),

• в результате анализа поведения автомата делается заключение о том, в каком состоянии находится автомат и каков закон его функционирования.

При этом предполагается, что исследователю известна таблица переходов/выходов исправного автомата и все варианты возможных таблиц, характеризующих неисправности автомата.

Пусть автомат A при любой возможной неисправности i=1,…,k превращается в один из автоматов {A₁,A₂,…,A_k}={A_i| i=1,…,k}. Тогда задача контроля данного автомата X, который должен работать как автомат A, заключается в выяснении соотношения X=A. Если XA,то X{A_i| i=1,…,k}. Задача диагностики заключается в определении i, при котором X=A_i.

Пример 7. Автомат A задан таблицей:

	s1 s2 s3
v1 v2	s2/w1 s3/w2 s1/w2 s3/w2 s1/w1 s2/w1

или если использовать упрощенную запись, содержащую только индексы состояний, входных и выходных символов:

	1 2 3
1 2	2/1 3/2 1/2 3/2 1/1 2/1

Предположим, что возможны две неисправности, порождающие автоматы A₁ и A₂ соответственно:

Клетки таблиц для A₁ и A₂, отличающиеся от A, подчеркнуты. Рассмотрим объединение (A,A₁,A₂) автоматов A, A₁ и A₂:

	1 2 3 11 21 31 12 22 33
1 2	2/1 3/2 1/2 21/1 31/1 11/2 22/1 32/2 12/1 3/2 1/1 2/1 31/2 11/1 21/1 32/2 12/1 22/1

Проведем установочный эксперимент с автоматом (A,A₁,A₂), т.е. такой эксперимент, который позволит по выходной последовательности однозначно определить состояние, в котором оказался автомат, причем неизвестное начальное состояние может быть любым из множества {1, 2, 3, 1₁, 2₁, 3₁, 1₂, 2₂, 3₃}. Для автомата (A,A₁,A₂) одной из возможных входных установочных последовательностей является v₁v₁v₁v₂v₂, или 11122 (табл.9).

Таблица 9

Начальное состояние	Реакция автомата (выходная последовательность)	Конечное состояние
1 2 3 11 21 31 12 22 33	12221 22112 21211 11221 12112 21111 12121 21112 11211	2 3 1 21 31 11 22 32 12

В данном примере реакция автомата (A,A₁,A₂) на входную последовательность 11122 позволяет однозначно установить начальное и конечное состояния автомата, т.е. последовательность 11122 является установочной.

Эта последовательность позволяет установить неисправность автомата A, т.е. осуществить диагностику автомата, т.е. является ли испытуемый автомат X автоматом A, A₁ или A₂.

Для контроля автомата, т.е. для определения истинности утверждения, что X=A, можно использовать более короткую входную последовательность v₁v₁v₁, или 111. Предполагается, что множество возможных неисправностей то же, что и в вышеприведенном примере (таблица 9).

Таблица 10 (контролирующая)

Начальное состояние	Реакция автомата (выходная последовательность)	Результат
1 2 3 11 21 31 12 22 33	122 22- 212 11- 121 211 121 211 11-	исправен исправен неисправен неисправен неисправен неисправен неисправен неисправен неисправен

Из таблицы 10 видно, что входные последовательности можно в отдельных случаях прерывать, т.к. в данном примере не обязательно подавить 3 входных символа, в отдельных случаях достаточно двух.

Построение установочных последовательностей

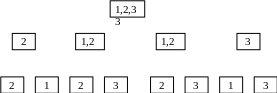
Пример 8. Для автомата A из предыдущего примера можно построить орграф, начальная вершина (исток) которого соответствует множеству S={s₁,s₂,s₃} возможных состояний. Из этой вершины выходят стрелки, ведущие в подмножества множества S, соответствующие парам x_i/y_i таблицы 9. Стоки орграфа соответствуют отдельным состояниям ( рис.7).

Таким образом, если входной символ 1, выходной символ 1, то автомат A перешел в состояние 2. Если на вход снова подать символ 1, то на выходе должен быть символ 2; в противном случае автомат неисправен (см.контролирующую таблицу 10).

Резюме: мы рассмотрели диагностику абстрактного автомата т.е., только диагностику закона функционирования. Диагностика от дельных элементов автомата не рассмотрена.

Для контроля автомата достаточно проверить правильность функционирования.

1 /2 1 /2 2/1 2/2

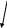
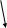
1/1 1 /2 2/1 2/2 1/1 1 /2 2/1 2/2

Рис. 7