Программирование на авм.

Этапы программирования

Процесс решения задачи на (АВМ) содержит следующие этапы:

• постановка задачи ;

• математическое описание реального объекта (оригинала);

• составление схемы модели и расчет ее параметров;

• набор и настройка составленной схемы на АВМ;

• пробное решение;

• коррекция и пересчет в случае необходимости;

• обработка результатов решения.

Математическое описание оригинала может быть представлено системой алгебраических и дифференциальных уравнений или в виде структурной схемы, в которой свойства динамических звеньев описаны их передаточными функциями. В соответствии с этим различают моделирование по уравнениям и по структурной схеме ( структурное моделирование).

• Принцип моделирования по уравнениям сводится к преобразованию их к виду, удобному для моделирования. Дифференциальные уравнения записываются относительно производных, а алгебраические - относительно переменных, необходимых для вычисления производных.

• При структурном моделировании по передаточным функциям задача сводится к определению коэффициентов передачи операционного усилителя в сравнении с моделью типового звена. Применение этого метода целесообразно в тех случаях, когда трудно или нецелесообразно переходить от передаточной функции к дифференциальному уравнению.

Масштабирование

П ри подготовке задачи необходимо с помощью масштабов установить связь между реальными и машинными переменными. Для обозначения машинной переменной используют дополнительный знак ~ :, ,

г де - реальная переменная;

- машинная переменная;

- масштаб переменной .

При масштабировании необходимо выделять зависимые и независимые переменные. Зависимые переменные в системах электропривода – ток, напряжение, момент и т.д.

При расчетах динамических режимов реальной независимой переменной является время. В АВМ ей соответствует машинное время.

М асштабы для зависимых переменных на основании выражения определяются по следующему соотношению:

,

где - максимальное значение машинной переменной ( для АВК - 31 это 10 В);

- максимальное значение реальной переменной.

М асштаб времени, связывающий независимую переменную t с машинным временем τ:

При mτ < 1 процесс на модели будет протекать быстрее, при mτ > 1 - медленнее, чем реальный процесс. Если mτ = 1 система моделируется в реальном масштабе времени. Это позволяет в ряде случаев лучше воспринимать ход исследуемого процесса, а также обеспечивает стыковку моделирующей установки с реальными физическими объектами.

П рактически mτ можно определить из следующего соотношения:

где =1-100 - желаемое время расчета на АВМ;

- время переходных процессов

в реальной системе.

Для выбора масштабов необходимо ориентировочно знать максимальные значения всех реальных переменных и время переходного процесса. Для удобства работы с моделью масштабы желательно округлять (для зависимых переменных только в сторону уменьшения).

Методика моделирования по уравнениям сводится к следующему:

а ) производится замена реальных переменных на машинные с использованием масштабов, учитывая, что оператор моделируемого уравнения и оператор моделирующей установки связаны следующим образом:

б) на основании полученного машинного уравнения составляется схема модели;

в) рассчитываются машинные коэффициенты.

Подготовка к решению на АВМ системы уравнений

С истемы уравнений, с помощью которых описываются динамические свойства реальных объектов, содержат дифференциальные и алгебраические уравнения. Методика подготовки не зависит от количества таких уравнений, поэтому для простоты рассмотрим систему, состоящую из одного дифференциального и одного алгебраического уравнения.

Для решения уравнений на АВМ их необходимо преобразовать к виду, удобному для моделирования. При этом дифференциальные уравнения записываются относительно производных, а алгебраические - относительно переменных, необходимых для вычисления производных.

П реобразованная система будет иметь вид

С истему уравнений для аналоговой модели получим, выразив переменные через масштабы Тогда

П реобразовав, получим

Коэффициенты к₁₁- к₂₂ называются машинными коэффициентами

Схему модели составляют следующим образом. По виду уравнения определяют тип ОУ: алгебраические решаются на сумматорах, а дифференциальные на интеграторах или интегросумматорах. Количество входов каждого ОУ равно числу членов правой части соответствующего уравнения.

Если имеются нелинейные математические операции (например умножение), то необходимо использовать соответствующие блоки. Затем схема модели дополняется инверторами для согласования знака переменных.

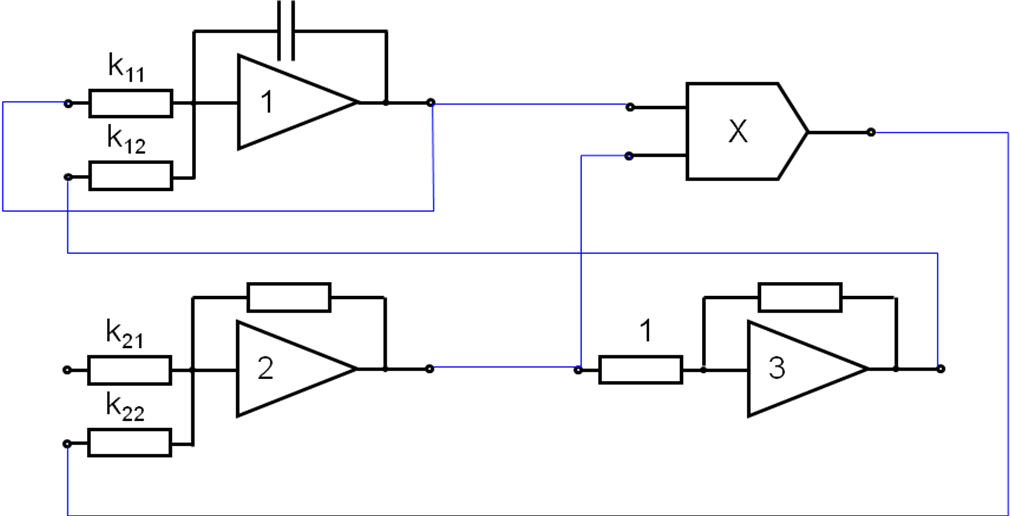
Н еобходимо помнить, что ОУ инвертирует знак, поэтому на выходе получаются не те переменные, которые указаны в левой части уравнений, а инверсные. Для расчета машинных коэффициентов можно пользоваться общими формулами:

для суммирующих ОУ

для интегрирующих ОУ

m_вх и m_вых - масштабы переменных на входе и выходе ОУ

ВОПРОС №4.