7. Позиционные системы счисления, запись и расчёт значения числа в них.
Система счисления – это способ записи чисел с помощью заданного набора специальных знаков ( чаще всего цифр) Существуют позиционные и непозиционные системы счисления.
Позиционная систе́ма счисле́ния (позиционная нумерация) — система счисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда).
Основой системы исчисления называется число, означающее, во сколько раз единица следующего разряда больше чем единица предыдущего.
В позиционной системе счисления любое вещественное число в развернутой форме может быть представлено в следующем виде:
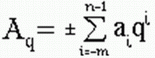
q - основание системы счисления,
ai -цифры, принадлежащие алфавиту данной системы счисления,
n - число целых разрядов числа,
m - число дробных разрядов числа.
Десяти́чная систе́ма счисле́ния — позиционная система счисления по целочисленному основанию 10. Одна из наиболее распространённых систем. В ней используются цифры 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, называемые арабскими цифрами. Предполагается, что основание 10 связано с количеством пальцев рук у человека.
Восьмери́чная систе́ма счисле́ния — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.
Восьмеричная система часто используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты двоичных. Ранее широко использовалась в программировании и вообще компьютерной документации, однако в настоящее время почти полностью вытеснена шестнадцатеричной.
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 1010 до 1510, то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
8.Перевод чисел из одной системы счисления в другую – перевод чисел с основанием ,являющимся степенью 2, перевод целый и дробных чисел по правилам, по степенному ряду, по схеме Горнера.
Перевод чисел с основаниями, являющимися степенью числа 2.
Если между основаниями p и q соблюдается связь p^1=q^k, где k -целое, то каждая цифра с основание p представляется k цифрами алфавита основания q
Так как 8^1=2^3, то каждая цифра восьмеричного числа будет представлена тремя двоичными цифрами (триадами), и наоборот, триада (от запятой влево и вправо) заменяется восьмеричной цифрой.
Перевод целых чисел из одной системы в другую.
Правила перевода.
1)Последовательно делить данное число и получаемые целые частные на основание новой системы счисления, выраженные цифрами исходной системы, до тех пор, пока частное на станет равным нулю;
2)Полученные остатки, являющимися цифрами числа в новой системе счисления, выразить цифрами алфавита новой системы счисления;
3)Составить число в новой системе счисления, начиная с последнего остатка.
Правила перевода дробных
1)Последовательно умножать данное число и получаемые дробные части произведений на основание новой системы, выраженное цифрами исходной системы, до тех пор, пока дробная часть произведения не станет равной нулю или до точности исходного числа, если дробь бесконечная;
2)Полученные целые части произведений, являющиеся цифрами числа в новой системе, выразить цифрами алфавита новой системы;
3)Составить дробную часть числа в новой системе, начиная с целой части первого произведения.
По степенному ряду
Любую систему счисления можно перевести по степенному ряду.
255,528 = 2·8^2+5·8^1+5·8^0+5·8^-1+2·8^-2 = 173,6562510
По схеме Горнера.
10101101 2 = ((((((1·2+0)·2+1)·2+0)·2+1)·2+1)·2+0)·2+1 = 173 10
0,10101 2 = 0,5(1+0,5(0+0,5(1+0,5(0+1·0,5)))) = 0,65625 10
9.Сложение и вычитание двоичных, восьмеричных и шестнадцатеричных чисел.
Двоичн)Все арифметические операции над двоичными числами можно свести к 2-м операциям: сложению и сдвигу кодов. Это позволяет технически реализовать четыре арифметических действия в одном арифметико-логическом устройстве, используя одни и те же электронные схемы. Впрочем, и в десятичной арифметике в конечном итоге выполняются те же действия – сложение и сдвиг.
Восьмиричн)При выполнении действий сложения и вычитания в 8-ной системе счисления необходимо помнить: в записи результатов сложения и вычитания могут быть использованы только цифры восьмеричного алфавита;основание восьмеричной системы счисления равен 8, т.е. переполнение наступает, когда результат сложения больше или равен 8. В этом случае для записи результата надо вычесть 8, записать остаток, а к старшему разряду прибавить единицу переполнения; если при вычитании приходится занимать единицу в старшем разряде, эта единица переносится в младший разряд в виде 8 единиц.
Шест)При выполнении действий сложения и вычитания в 16-ной системе счисления необходимо помнить: в записи результатов сложения и вычитания могут быть использованы только цифры шестнадцатеричного алфавита (0-9, A-F) Основание шестнадцатеричной системы счисления равно 16, т.е. переполнение наступает, когда результат сложения больше или равен 16. В этом случае для записи результата надо вычесть 16, записать остаток, а к старшему разряду прибавить единицу переполнения; если при вычитании приходится занимать единицу в старшем разряде, эта единица переносится в младший разряд в виде 16 единиц.
10.Умножение и деление двоичных, восьмеричных и шестнадцатеричных чисел
Двоич)Умножение и деление производится поразрядно и сводятся к двум операциям: сложению и сдвигу. Деление так же можно представить как выполнение операций сложения и сдвига.
Восьм)Чтобы умножить одно восьмеричное число на другое, требуется использовать восьмеричную таблицу умножения (табл. 12.1). Она позволяет умножать числа аналогично тому, как это делается в десятичной системе счисления.