4) Переход к пределу n дает решение задачи

S_бок = lim S(n) = 2 f(x) ( 17 )

V = lim V(n) = f²(x) dx ( 18 )

П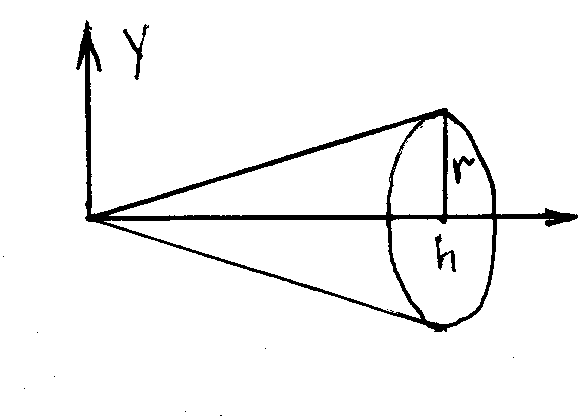 р. Определить площадь боковой поверхности и объем кругового конуса высоты h и радиуса основания r .

Решение. Уравнение образующей y = r/h x , где 0 <x < h. Тогда y’ = r/h , =

S_бок = 2 r/h x dx = r = rl

V = (r/h)² x² dx = h r² / 3

Устные экзаменационные вопросы

по теме: «Неопределенный и определенный интегралы, КЧ »

Повторение : 1) Опр. функции; 2) Опр. сложной функции, перечислить ее элементы; 3) Опр. производной по Коши и по Ньютону, её алгебраический, физический, геометрический смысл; 4) Перечислить правила дифференцирования; 5) Опр. дифференциала, правило его вычисления.

1. Опр. первообразной функции и неопределенного интеграла.

2. Перечислить названия элементов, входящих под знак неопределенного интеграла.

3. Сколько первообразных имеет каждая функция и почему?

4. Перечислить основные свойства неопр. интеграла.

5. Объяснить инвариантность формы дифференциала сложной функции и неопр ин-ла.

6. Что такое непосредственное интегрирование ?

7. В чем заключается идея метода замены переменных ?

8. Вывод формулы интегрирования по частям.

9. Основная теорема алгебры.

10. Опр. рациональной алгебраической дроби. Переход от неправ-ой к прав-ой дроби.

11. Записать формулу разложения рац-ой алгебр-ой дроби на сумму простых дробей.

12. Общее правило при линейной замене переменных.

13. Перечислить основные виды замены переменных в интегралах от тригон. функций.

14. Правила вычисления интегралов с линейными и квадратичными иррациональностями.

15. Опр. аддитивной величины.

16. Алгоритм метода интегральной суммы.

17. Опр. интегральной суммы.

18. Опр. криволинейной трапеции.

19. Опр. определенного интеграла. Его геометрический и физический смысл.

20. Перечислить основные свойства определенного интеграла. Теорема о среднем.

21. Опр. интеграл с переменным верхним пределом. Его вид и общее свойство.

22. Доказать формулу Ньютона-Лейбница. Ее значение в мат. анализе.

23. Опр. несобственного интеграла 1 и 2 рода. Общее правило вычисления интеграла от разрывных функций.

24. Общие правила вычисления площади плоской фигуры.

25. Площадь криволинейного сектора в полярных координатах. Записать интегральную сумму и интеграл.

26. Длина произвольной дуги. Записать интегральную сумму и интеграл.

27. Боковая поверхность и объем тела вращения. Записать интегральную сумму и интеграл.

8